GhostNet 论文解读
GhostNet: More Features from Cheap Operations. CVPR 2020.
论文地址：arXiv
开源 PyTorch代码：GitHub
引言
由于嵌入式设备上有限的内存和计算资源，很难在上面部署卷积神经网络。因此，深度神经网络设计最新的趋势是探索轻量级高效网络体系结构的设计。那些成功的CNN模型一个重要的特征是特征图冗余，但是大量甚至冗余的信息通常可以确保对输入数据的全面了解。
文章提出了一个新颖的模型（Ghost）,可以通过廉价的操作生成更多的feature maps。基于一组原始的特征图，作者应用了一系列线性变换，来生成许多完全可以从原始特征发掘所需信息的ghost feature maps。所提出的Ghost模块可以作为即插即用组件来升级现有的卷积神经网络。Ghost bottlenecks可以被设计用来堆叠Ghost 模块，从而可以形成轻量级的网络GhostNet。文中指出，GhostNet在ImageNet 2012分类数据集上的top1准确率（75.7%）比MobileNet v3（75.2%）还要高，却拥有着相似的计算量。
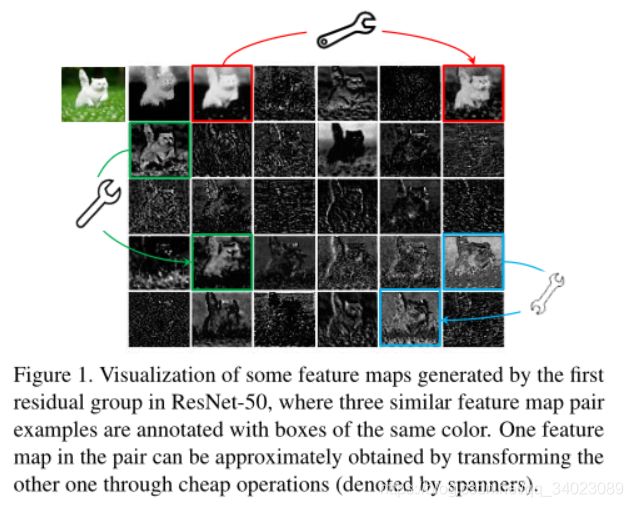
如上图所示，以在ResNet-50为例，将经过第一个残差块处理后的特征图拿出来，可以看到其中存在许多相似的特征映射对，例如彼此重影。本文做的不是避免使用多余的特征图，而是倾向于以节省成本的方式包含它们。
深度卷积神经网络通常由大量卷积组成，从而导致大量的计算成本。尽管最近的工作，例如MobileNet和ShuffleNet已经引入了深度卷积或混洗操作，以使用较小的卷积滤波器（浮点数运算）来构建有效的CNN。其余1×1卷积层仍将占用大量内存和FLOPs。
Ghost模块
输入数据 X ∈ R c ∗ h ∗ w \quad X\in\mathbb R^{c*h*w} X∈Rc∗h∗w ，其中c是输入数据的通道，h和w是输入数据的高和宽，则生成n个特征图的任意卷积层可以表示为 Y = X ∗ f + b \quad Y=X*f+b Y=X∗f+b，其中 Y ∈ R h ′ ∗ w ′ ∗ n \quad Y\in\mathbb R^{h^{'} *w^{'} *n} Y∈Rh′∗w′∗n是具有n个通道的输出。 f ∈ R c ∗ k ∗ k ∗ n \quad f\in\mathbb R^{c*k*k*n} f∈Rc∗k∗k∗n，其中 h ′ \quad h^{'} h′和 w ′ \quad w^{'} w′是输出特征图的高和宽， k ∗ k \quad k*k k∗k是卷积滤波器 f \quad f f的内核大小。在这个卷积操作中，FLOPs的计算量是 n ∗ h ′ ∗ w ′ ∗ c ∗ k ∗ k \quad n*h^{'}*w^{'}*c*k*k n∗h′∗w′∗c∗k∗k。由于c和n的值通常都非常大，所以FLOPs非常大。
本文指出，不必一一生成具有大量FLOP和参数的冗余特征图。
根据上述公式，要优化的参数数量（ f \quad f f和 b \quad b b中的参数）由输入和输出特征图的尺寸确定。卷积层的输出特征图通常包含很多冗余，并且其中一些可能彼此相似。作者认为没有必要一一生成带有大量FLOPs和参数的冗余特征图。输出特征图是少数原始特征图通过一些廉价转换的“幻影”。这些原始特征图通常具有较小的大小，并由普通的卷积核生成。具体的，m个原始特征图 Y ′ ∈ R h ′ ∗ w ′ ∗ m \quad Y^{'}\in\mathbb R^{h^{'}*w{'}*m} Y′∈Rh′∗w′∗m通过一次普通的卷积生成： Y ′ = x ∗ f ′ \quad Y^{'}=x*f^{'} Y′=x∗f′，其中 f ′ ∈ R c ∗ k ∗ k ∗ m ， m < = n \quad f^{'}\in\mathbb R^{c*k*k*m}，m<=n f′∈Rc∗k∗k∗m，m<=n。为了简单表示省去了偏置项。filter size，stride，padding等参数的设置和原始的卷积是一样的，以保证输出特征图的 h ′ 和 w ′ \quad h^{'}和w^{'} h′和w′是一样的。
为了获取n个输出特征图，本文提出对 Y ′ \quad Y^{'} Y′中的每个原始特征应用一系列廉价的线性运算，以生成 s \quad s s个幻影特征图。
y i , j = Γ i , j ( y i ′ ) ， ∀ i = 1 , . . . . . . m ， j = 1 , . . . . . . s \ y_{i,j}=\Gamma_{i,j}(y_i^{'})，\forall i=1,......m，j=1,......s yi,j=Γi,j(yi′)，∀i=1,......m，j=1,......s其中 y i ′ \ y_i^{'} yi′是 Y ′ \ Y^{'} Y′的第i个原始特征图， Γ i , j \Gamma_{i,j} Γi,j是生成第j个幻影特征图 y i , j \ y_{i,j} yi,j的第j个线性变换（除了最后一个）。也就是说 y i ′ \ y_i^{'} yi′可以有一个或者多个幻影特征图 ( y i , j ) j = 1 s \ ( y_{i,j})_{j=1}^s (yi,j)j=1s。最后一个 Γ i , s \Gamma_{i,s} Γi,s是直连操作用来保持原有的特征图。通过使用廉价操作，我们可以获得 n = m ∗ s \ n=m*s n=m∗s个特征图 Y = [ y 11 , y 12 , y 13 , . . . . . . , y m , s ] \ Y=[y_{11},y_{12},y_{13},......,y_{m,s}] Y=[y11,y12,y13,......,ym,s] 作为Ghost模块的输出数据。
注意到线性运算在每个通道上进行运算，其计算成本比普通卷积要小得多。作者在实验中也尝试了在Ghost模块中采用有几种不同的线性运算，例如3×3和5×5线性核。
复杂度计算
理想情况下，线性运算可以具有不同的形状和参数，但是考虑到CPU和GPU卡的使用，不同的形状和参数会阻碍在线推理。作者建议在一个Ghost模块中采用相同大小的线性运算以高效实施。具体来说，Ghost模块具有一个恒等映射和 m ∗ ( s − 1 ) \ m*(s-1) m∗(s−1) 个线性运算，并且每个线性运算的平均内核大小为 d ∗ d \ d*d d∗d。
使用Ghost模块替代普通卷积操作的理论加速比为：
理论压缩比：（等于加速比）
构造高效的网络模型
Ghost Bottlenecks 。 利用Ghost 模块的优势，作者介绍了专门为小型CNN设计的Ghost瓶颈（G-bneck）。
提出的ghost bottleneck主要由两个堆叠的Ghost模块组成。第一个Ghost模块用作扩展层，增加通道数。第2个Ghost模块进行降维，与直连的通道数匹配。在每一层之后都应用了BN和ReLU，除了在第2个Ghost模块之后不使用ReLU。两个Ghost模块之间使用了深度可分离卷积。
GhostNet
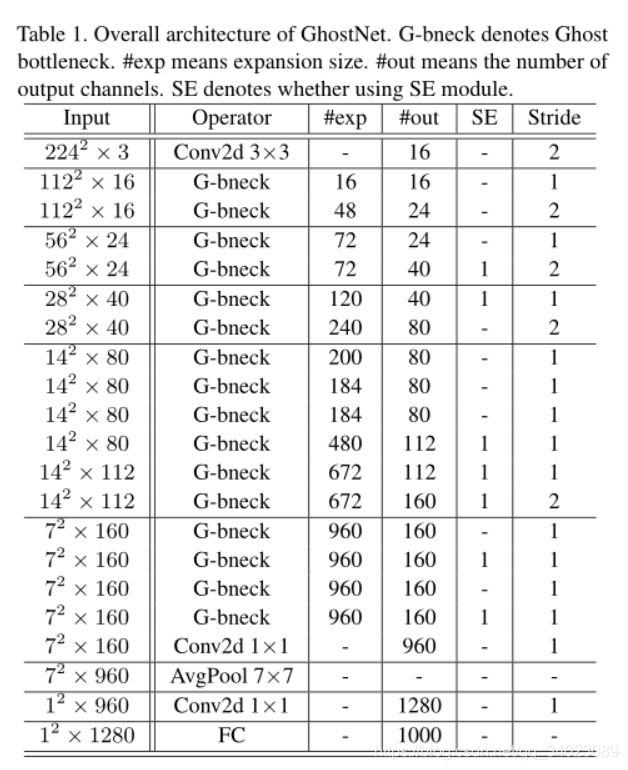
作者基本上遵循MobileNetV3的体系结构，并用Ghost bottleneck替代MobileNetV3中的bottleneck。
实验结果
Ghost模块具有两个超参数，s用于生成 m = n / s \ m=n/s m=n/s 个内在特征图，以及用于计算幻影特征图的线性运算的 d ∗ d \ d*d d∗d（即深度卷积核的大小）。作者测试了这两个参数的影响。
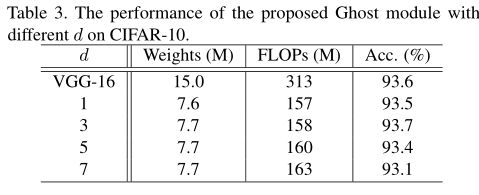
首先，作者固定 s \ s s并在{1,3,5,7}范围中调整 d \ d d ，并在表3中列出CIFAR-10验证集上的结果。作者可以看到，当 d = 3 \ d=3 d=3 的时候，Ghost模块的性能优于更小或更大的Ghost模块。这是因为大小为 d = 1 \ d=1 d=1 的内核无法在特征图上引入空间信息，而较大的内核（例如 d = 5 \ d=5 d=5或 d = 7 \ d=7 d=7 ）会导致过拟合和更多计算。因此，在以下实验中作者采用 d = 3 \ d=3 d=3来提高有效性和效率。
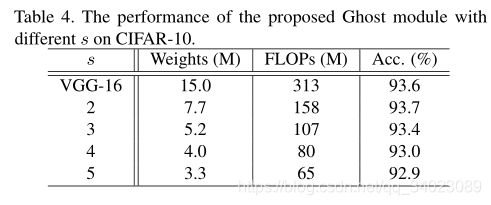
在研究了内核大小的影响之后，作者固定 d = 3 \ d=3 d=3并在{2,3,4,5}的范围内调整超参数 s \ s s 。实际上， s \ s s 与所得网络的计算成本直接相关，即，较大的 s \ s s 导致较大的压缩率和加速比。从表4中的结果可以看出，当作者增加 s \ s s 时，FLOP显着减少，并且准确性逐渐降低，这是在预期之内的。特别地，当 s = 2 \ s=2 s=2 ，也就是将VGG-16压缩 2 ∗ \ 2* 2∗ 时，Ghost模块的性能甚至比原始模型稍好，表明了所提出的Ghost模块的优越性。
