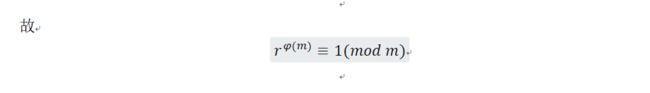从一条同余基本定理讲到欧拉定理

从一条同余基本定理讲到欧拉定理

参考使用资料为清华大学出版社的《信息安全数学基础教程(第2版)》(许春香)

前言

最近在复习密码学，遇到了一些不太懂的理论，遂又把之前的基础教程拿出来复习。俗话说，温故而知新，重新审视之前忽视的细节和思考一些定理，竟收获良多。在这里写一篇博客，权当读书笔记，同时向各位学习此内容的网友分享我的角度和见解。本篇主要想解释欧拉定理的证明过程，全篇内容是按照一个详细思考过程来记叙的，可能较为繁琐累赘，请见谅。

从最简单的定理说起

学习同余，就离不开学习它的计算规则。何为同余？字面理解就是对某个整数拥有相同余数的一对数字。那么书上在P16页的5个定理中有了这样的一条：

如果ac≡bc(mod m),且(c,m)=1,则a≡b(mod m)

看似理所当然的结论，其实暗含天机。我们可以这样来理解这个表达式：
先假设存在a mod m，b mod m，和整数c。现在有ac≡bc(mod m)。我们绘制一个简陋的图：
[····a········b········][······················][······················] …
图中将数轴分割成一个个大小为m的完全剩余系，剩余系中的元素用·表示，并特别标注a和b在剩余系中的位置（假设a [······················]…[·············ac·········]…[·············bc·········] …
根据前提的条件，此时ac和bc是同余的，也就是说，bc-ac可以被m整除。用公式表示为：m|bc-ac.
这说明，a和b的距离扩大c倍后可以被m整除，即m|(b-a)c，以此得出以下几种可能性：(b-a)和m互素、c和m互素、(b-a)和c*和m都不互素。否则不能被m整除。
于此，选择c和m互素的条件，就会得到一个很有用的结论：(b-a)可以整除m，于是：a≡b(mod m)。
这条结论放在之前介绍，是因为这仅仅作为一个引子，或者一个工具存在。无论多么复杂的体系，多么伟大的结论，都是在这些简单且看似微不足道的基础理论上构建而成。只有在这个过程中，似乎才能体会到它们的奇幻、神秘和波澜壮阔。

来说一说简化剩余系

这里要从俩个方面来叙述这个问题：一是什么是简化剩余系，二是为什么要提出简化剩余系。
首先第一个问题：什么是简化剩余系？

这里引用教材原话：

如果一个模m的剩余类里面的数与m互素，则称它为与模m互素的剩余类。从与模m互素的每个剩余类中各取一个数构成的集合称为模m的一个简化剩余系。

通俗理解就是，拿出每个剩余类里和m互素的数字，组成个集合就是简化剩余系。此外，其数字个数为欧拉函数φ(m)。

那么，为什么要提出这个东西来呢？从后续的剧情来看，这个东西在欧拉定理里占了举足轻重的一环。人们创造出这个概念的时候，也许是察觉到了互素的特殊性带来的一些性质，于是希望创建一个天生具有该性质的群，将其变成在一个集合内泛用的前提。基于这种特殊性，一些神奇的性质渐渐被发掘出来，其中就有引出欧拉定理的“罪魁祸首”：

定理6-3 设a是一个整数且(a,m)=1。如果x跑遍模m的一个简化剩余系，则ax也跑遍模m的简化剩余系。

“如果x跑遍模m的一个简化剩余系”说明x是一个简化剩余系的任意一员。翻译成大白话就是，对于一个简化剩余系里的每一个数，同乘上一个和m互素的数，最后结果也必定还是m的一个简化剩余系。

看似理所当然，其实并不理所当然。为什么要乘一个和m互素的数？首先根据定理，(a,c)=1，(b,c)=1，则(ab,c)=1，所以ax必然是一个简化剩余系里的元素，但难道就不会出现两个同余的结果吗？

有趣的是，证明过程就用到了最基本的结论。上面说了， 如果ac≡bc(mod m),且(c,m)=1,则a≡b(mod m)。由于a是与m互素的数，满足了条件，所以如果出现ax1 ≡ax2(mod m)的情况，那么x1 ≡x2(mod m)。很明显，在一个简化剩余系里，是不可能出现2个同余的数字的，所以由ax可以构成简化剩余系。

至此，一切准备工作就绪，谁能想到，这些简单至极的理论将会引出将来对密码学产生如此重要作用的欧拉定理呢？

Origin：欧拉定理

我想说，欧拉定理作为一个结论，从来不复杂，作为密码学等相关领域的继承者，也许学会如何使用比理解起源更重要、更省力气。然而，不去了解本质的理论是空洞的，只有摸索和探求定理的诞生和成熟的过程，才会真正认识到其精彩之处。

欧拉定理：

设m是正整数，如果(r,m)=1，则r^φ(m)≡1(mod m)。

翻译过来就是：简化剩余系里任意一个元素，其最多φ(m)次幂的模m为1。简单粗暴的结论。一点都不拖泥带水。其数论上的证明过程有趣且玄幻：

到这里还算中规中矩。利用了上述的定理，说明了在简化剩余系中，同乘任意一个元素，还是会得到简化剩余系。
然而接下来笔锋一转：

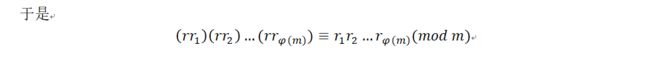
将新得到的简化剩余系的每个元素相乘。然而之后的证明行云流水，一气呵成：

到这里，似乎似曾相识。没错，在这里又要用到基本定理了：
如果ac≡bc(mod m),且(c,m)=1,则a≡b(mod m)
一切又回到了起点：