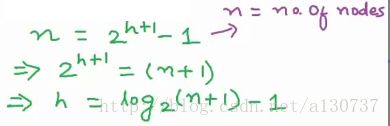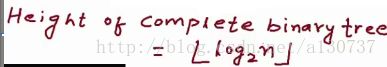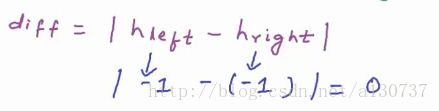C++ Binary Tree(二叉树)

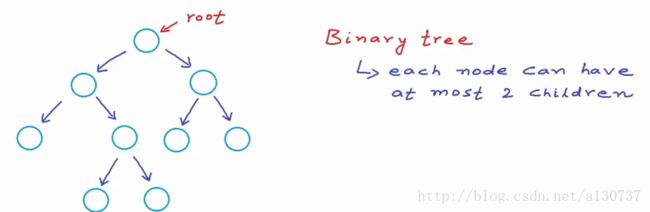
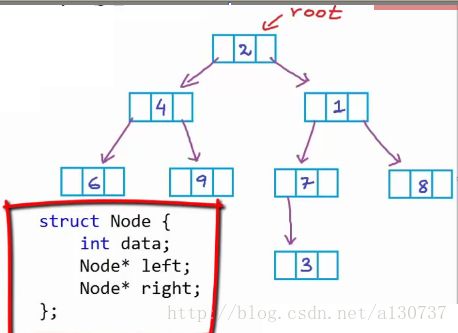
一个二叉树是有节点（node）组成的。 二叉树（binary Tree）中的每一个节点都包含一个“left” pointer, 一个“right” pointer,  和一个data element。 根节点指针（root pointer） 指向树的最顶点的那个节点（即root node）. the left pointers and right pointers 递归的recursively）指向 两边的子树。

 一个空指针（Null pointer） 可以代表一个没有element的二叉树（binary Tree）， 即empty Tree.。

   binary tree 的正式的递归定义（formal recursive definition) 如下：

一个二叉树要么是一个empty tree（即一个空指针）（base case）, 要么有一个单个节点， 其左右指针分别递归指向一个二叉树（binary tree）。

 

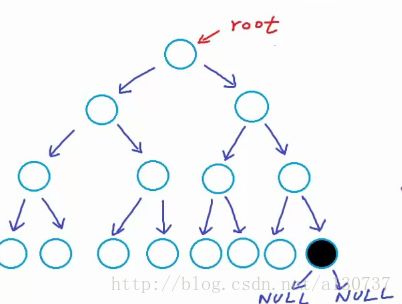
上面的这棵树也被称为strict binary tree(严格二叉树)， 因为除了叶子节点， 每个节点有且只有两个childre 节点。

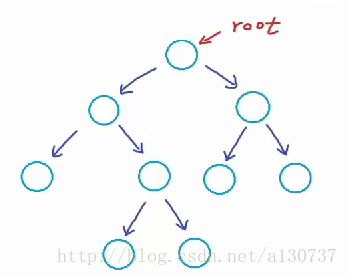
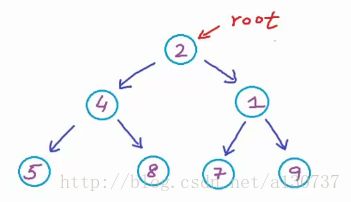
下图也是一个binary tree：

 

 

下面对二叉树进行分类。

（1） strict / proper binary tree:  每一个节点都有0 或者2个child

 

(2) complete binary tree(完备二叉树):  All levels except the last are completely filled and all nodes are as left as possible.

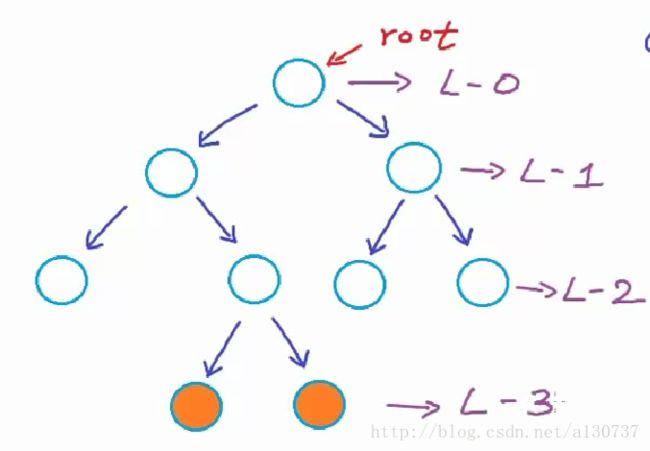
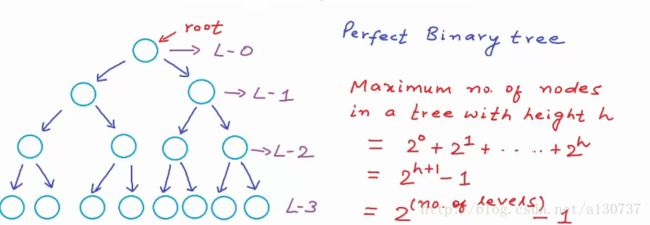
Q： 什么是level呢？

A： 具有相同的深度（depth）的节点被称为处于同一个level。 根节点的深度是0， 我们说根节点所处的level 为 level 0, 依次类推。

上图中， 最大的level是3》 树的高度(height)是树的最大的level， 即也是3.

下面注意一个性质： level i 可能具有的最大的节点数目是： 2^i。

 

也就是说， level0 ， 至多有1个节点（根节点）。

level1， 至多有2个节点， 等等。

 

知道了这些知识， 我们就不难理解什么是complete binary tree(完备二叉树)了。

也就是说， 除了最后一个level， 其余上面的所有level 都必须是filled.（即level 从上到下为1， 2， 4， 8， 16， 。。。。）。 最后一个level未必需要filled, 但是节点必须是as left as possible。

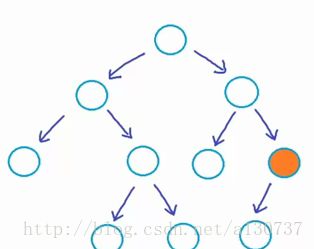
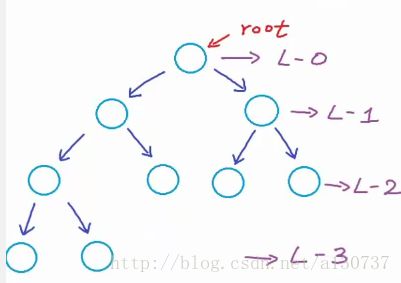
 Q： 上面的那个二叉树是否为二叉树？

A： 不是的， 因为最后一层的树的节点不是as left as possible ， 所以不是。

 

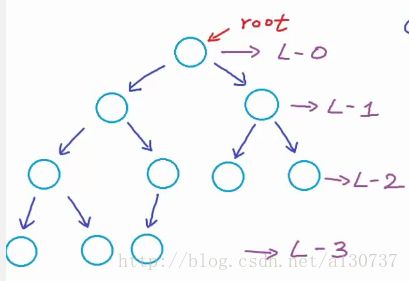
下图也是一个完备的二叉树：

下图同样是一个complete binary tree：

 

 

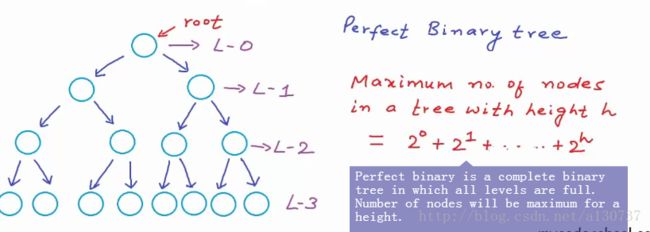
（3）perfect binary tree（完美二叉树）：首先， 完美二叉树是完备二叉树的一种（特殊情况）。  如果所有的level(包括最后一个level)都是填充满的（fillled)， 我们就说这是一个完美二叉树， 这也是平衡二叉树（balanced binary tree）的特殊情况, 因为对于每一个level i, 节点数目都要达到： 2^i, 如下图：

 

当给定level 的一个完备二叉树是完美二叉树的时候， 节点数目达到最大值。 当给定我们完备二叉树的节点的数目的时候， 我们通过解方程可以求出树的高度和levels 的数目：

 

举个例子， 对于具有15个节点的完备二叉树， 树的高度是log(15 + 1) - 1 = 3， 参见上图。

一般而言， 对于完备二叉树， 给定节点数目， 我们可以按照如下计算其高度， 如下：

 

 

 

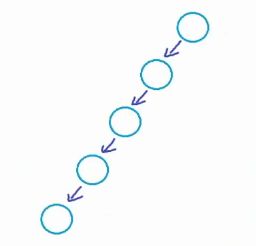
关于树的很多的操作（例如插入， 删除， 搜索）的时间复杂度都和一棵树的高度有着密切的关系。例如对于BST（binary search tree）， insertion, deletion, search 等操作和树的高度是成正比的。 所以我们希望我们的树的高度是最矮的。 当树接近于完美二叉树的时候， 高度是最小的。 所以我们总是希望我们的树时dense 的。 如下图， 就是一个sparse tree:

所以对于一个具有n个节点的二叉树， 树可能的最大的高度为n-1, 最小的高度为floor(logn)（下高斯函数）。  我们当然希望我们的树时越矮越好， 这样， 我们对于树的各种操作的的时间复杂度就可能降至O（logn）。

 

 

（4）平衡二叉树（balanced binary tree）

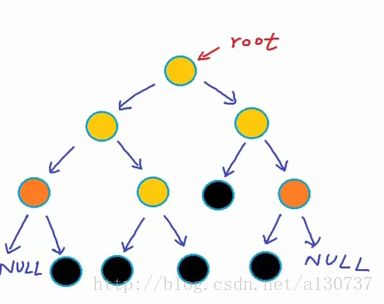
 例如， 对于下图黑色的叶子节点：

这个节点的左子树的高度和右子树的高度只差为0：

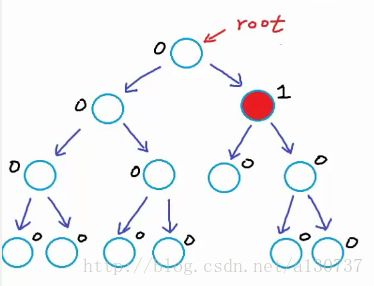
在比如， 对于下图：

这棵树仍然十一个平衡树。 具体每个节点的左子树高度和右子树的高度差如上图标记。

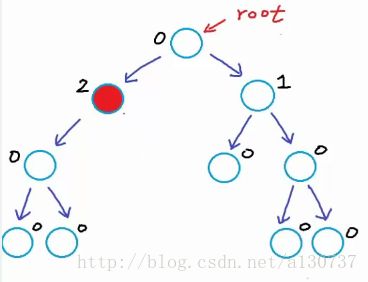
然而下图就不是平衡二叉树了。 因为对于节点（红色标记）， 左子树（高度为1）的和右子树（高度为-1）的高度差为2（1 - （-1） = 2）。

 

 

 

平衡树很重要。 我们常常要求我们创建的的树是平衡的，因为对于给定的数目的节点（数据或者record大数目），  这样树时dens的， 树高度是最小的。

这样， 对于树的各种操作， 例如插入， 查找元素， 删除等操作， 会更加的高效。

 

 

介绍了上面的关于二叉树的几大内容， 接下来， 我们分析如何去implement 一个binary tree(换句话说， 就是如何存储我们的树的数据)。

主要有如下三步：

（1）dynamically create nodes(即动态创建树的节点)

上述的方法是对常见的树的实现方法。

 

（2）在某些特殊情况下， 也可以使用Arrays， 通常用于存储完备二叉树。

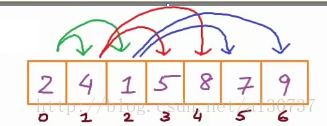
例如对于下面的一棵完备二叉树树（binary tree of integers）：

 

 

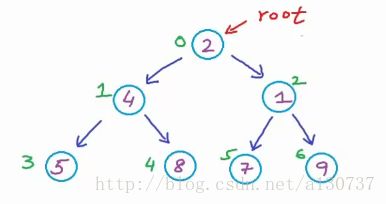
接下来， 我们对各个节点进行level by level 的按照如下方式标记：

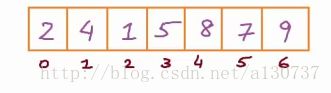
最后， 我们就可以用一个数组存储这棵完备二叉树了：

上述只是对二叉树数据的存储。 但是我们并没有存储数据之间linkes的关系信息。 接下来， 我们需要表示各个元素索引之间的关系了。 我们知道， 根节点的左孩子是4， 根节点的有孩子是1.。。。

对于完备二叉树而言， 这些关系都是隐含着的， 索引的关系如下：

 

即对于任何一个节点i(在数组中的索引）, 左孩子的索引是2*i +1, 右孩子的索引是2*i + 2。 注意， 这种关系只是对complete binary tree 有效的。我们将会在heap中详细谈到用array 实现的这样的一种二叉树（heap）。 （heap： a special kind of binary tree, 注意这里的heap 不是和stack 相对应的， 是二叉树中一种被称为heap的二叉树， 而非内存的一个区域了）。