python算法(基础)----栈
栈(有时称为“后进先出栈”)是一个项的有序集合
其中添加移除新项总发生在同一端。这一 端通常称为“顶部”。与顶部对应的端称为“底部”。这种排序原则有时被称为 LIFO。栈的底部很重要,因为在栈中靠近底部的项是存储时间最长的。
Figure 3 展示了 Python 数据对象创建和删除的过程,注意观察他们的顺序
想想这种反转的属性,你可以想到使用计算机的时候所碰到的例子。例如,每个 web 浏览器 都有一个返回按钮。当你浏览网页时,这些网页被放置在一个栈中(实际是网页的网址)。你现在查看的网页在顶部,你第一个查看的网页在底部。如果按‘返回’按钮,将按相反的顺序浏览刚才的页面。
栈的抽象数据类型:
栈操作如下
Stack() 创建一个空的新栈。 它不需要参数,并返回一个空栈。
push(item)将一个新项添加到栈的顶部。它需要 item 做参数并不返回任何内容。
pop() 从栈中删除顶部项。它不需要参数并返回 item 。栈被修改。
peek() 从栈返回顶部项,但不会删除它。不需要参数。 不修改栈。
isEmpty() 测试栈是否为空。不需要参数,并返回布尔值。
size() 返回栈中的 item 数量。不需要参数,并返回一个整数。
例如,s 是已经创建的空栈,Table1 展示了栈操作序列的结果。栈中,顶部项列在最右边。
Python实现栈:
在 Python 中,与任何面向对象编程语言一样,抽象数据类型 (如栈)的选择的实现是创建一个新类。栈操作实现为类的方法。此外,为了实现作为元素集合的栈,使用由 Python 提供的原语集合的能力是有意义的。 我们将使用列表作为底层实现。回想一下,Python 中的列表类提供了有序集合机制和一组方法。例如,如果我们有列表 [2,5,3,6,7,4],我们只需要确定列表的哪一端将被认为是栈的顶部。一旦确定,可以使用诸如 append 和 pop的列表方法来实现操作。以下栈实现假定列表的结尾将保存栈的顶部元素。随着栈增长(push 操作),新项将被添加到列表的末尾。 pop 也操作列表末尾的元素。
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)记住我们只定义类的实现,我们需要创建一个栈,然后使用它。下面代码展示了我们通过实例化 Stack 类执行 Table 1中的操作。注意,Stack 类的定义是从 pythonds 模块导入的。
from pythonds.basic.stack import Stack
s=Stack()
print(s.isEmpty())
s.push(4)
s.push('dog')
print(s.peek())
s.push(True)
print(s.size())
print(s.isEmpty())
s.push(8.4)
print(s.pop())
print(s.pop())
print(s.size())- 简单括号匹配:
括号必须以匹配的方式出现。括号匹配意味着每个开始符号具有相应的结束符号,并且括号能被正确嵌套。考虑下面正确匹配的括号字符串:(()()()()) (((()))) (()((())())) 对比那些不匹配的括号: ((((((()) ())) (()()(()
from pythonds.basic.stack import Stack
def parChecker(symbolString):
s = Stack()
balanced = True
index = 0
while index < len(symbolString) and balanced:
symbol = symbolString[index]
if symbol == "(":
s.push(symbol)
else:
if s.isEmpty():
balanced = False
else:
s.pop()
index = index + 1
if balanced and s.isEmpty():
return True
return False
print(parChecker('((()))'))
print(parChecker('(()'))- 符号匹配
混合符号(相互匹配):
{ { ( [ ] [ ] ) } ( ) }
[ [ { { ( ( ) ) } } ] ]
[ ] [ ] [ ] ( ) { }
不匹配:
( [ ) ]
( ( ( ) ] ) )
[ { ( ) ]
from pythonds.basic.stack import Stack
def parChecker(symbolString):
s = Stack()
balanced = True
index = 0
while index < len(symbolString) and balanced:
symbol = symbolString[index]
if symbol in "([{":
s.push(symbol)
else:
if s.isEmpty():
balanced = False
else:
top = s.pop()
if not matches(top,symbol):
balanced = False
index = index + 1
if balanced and s.isEmpty():
return True
else:
return False
#辅助函数匹配,匹配弹出的字符是否与当前字符互为相反字符
def matches(open,close):
opens = "([{"
closers = ")]}"
return opens.index(open) == closers.index(close)
print(parChecker('{
{([][])}()}'))
print(parChecker('[{()]'))- 十进制转换成二进制
十进制 23310 以及对应的二进制表示 11101001 2分别解释为:
和
![]()
但是我们如何能够容易地将整数值转换为二进制呢?答案是“除 2”算法,它用栈来跟踪二进制结果的数字。“除 2”算法假定我们从大于 0 的整数开始。不断迭代的将十进制除以 2,并跟踪余数。第一个除以 2 的余数说明了这个值是偶数还是奇数。偶数有 0 的余数,记为 0。奇数有余数 1,记为 1.我们将得到的二进制构建为数字序列,第一个余数实际上是序列中的最后一个数字。见 Figure 5 , 我们再次看到了反转的属性,表示栈可能是解决这个问题的数据结构。
#仅限二进制转换
from pythonds.basic.stack import Stack
def divideBy2(decNumber):
remstack = Stack()
while decNumber > 0:
rem = decNumber % 2
remstack.push(rem)
decNumber = decNumber // 2
binString = ""
while not remstack.isEmpty():
binString = binString + str(remstack.pop())
return binString
print(divideBy2(42))用于二进制转换的算法可以很容易的扩展以执行任何基数的转换。
#支持各级进制转换
from pythonds.basic.stack import Stack
def baseConverter(decNumber,base):
#创建一组数字,用来表示超过 9 的余数。
digits = "0123456789ABCDEF"
remstack = Stack()
while decNumber > 0:
rem = decNumber % base
remstack.push(rem)
decNumber = decNumber // base
newString = ""
while not remstack.isEmpty():
newString = newString + digits[remstack.pop()]
return newString
print(baseConverter(25,2))
print(baseConverter(25,16))- 中缀,前缀和后缀表达式
中缀:B*C 因为运算符在它处理的两个操作数之间。
前缀表达式符号要求所有运算符在它们处理的两个操作数之前。A+B*C 在前缀中写为 + A * B C 。乘法运算符紧接在操作数 B 和 C 之前,表示 * 优先 于 + 。在后缀中,表达式将是 A B C * + ,操作的顺序被保留,因为 * 紧接在 B 和 C 之后出现,表示 * 具有高优先级,+ 优先级低。
现在考虑中缀表达式 (A + B) * C ,回想下,在这种情况下,中缀需要括号在乘法之前强制执行加法。然而,当 A+B 写到前缀中时,加法运算符简单的移动到操作数 + A B 之前。这个操作的结果成为乘法的第一个操作数。乘法运算符移动到整个表达式的前面,得出 * + A B C ,同样,在后缀 A B + 中,强制先加法。可以直接对该结果和剩余的操作数 C 相乘。然后,得出后缀表达式为 A B + C * 。 再次考虑这三个表达式(见 Table 3),括号不见了。为什么在前缀和后缀的时候不需要括号了呢?答案是操作符对于他们的操作数不再模糊,只有中缀才需要括号,前缀和后缀表达式的操作顺序完全由操作符的顺序决定。
Table 4 展示了一些其他的例子
- 中缀表达式转换前缀和后缀
到目前为止,我们已经使用特定方法在中缀表达式和等效前缀和后缀表达式符号之间进行转换。正如你可能期望的,有一些算法来执行转换,允许任何复杂表达式转换。我们考虑的第一种技术使用前面讨论的完全括号表达式的概念。回想一下, A + B * C 可以 写成 (A +(B * C)) ,以明确标识乘法优先于加法。看上面的子表达式(B * C)中的右括号。 如果我们将乘法符号移动到那个位置,并删除匹配的左括号,得到 B C * ,我们实际上已经将子表达式转换为后缀符号。如果加法运算符也被移动到其相应的右括号位置并且匹配的左括号被去除,则将得到完整的后缀表达式(见 Figure 6)。
如果我们不是将符号移动到右括号的位置,我们将它向左移动,我们得到前缀符号(见 Figure 7)。圆括号对的位置实际上是包含的运算符的最终位置的线索。
所以为了转换表达式,无论是对前缀还是后缀符号,先根据操作的顺序把表达式转换成完全括号表达式。然后将包含的运算符移动到左或右括号的位置,具体取决于需要前缀或后缀符号。这里面有个更复杂的例子, (A + B) * C - (D - E) * (F + G) ,Figure 8 显示了如何转换为后缀和前缀。
- 中缀转后缀通用法
假设中缀表达式是一个由空格分隔的标记字符串。 操作符标记是 *,/,+ 和 - ,以及左右括号。操作数是单字符 A,B,C 等。 以下步骤将后缀顺序生成一个字符串。
1.创建一个名为 opstack 的空栈以保存运算符。给输出创建一个空列表。
2.通过使用字符串方法拆分将输入的中缀字符串转换为标记列表。
3.从左到右扫描标记列表。 如果标记是操作数,将其附加到输出列表的末尾。 如果标记是左括号,将其压到 opstack 上。 如果标记是右括号,则弹出 opstack,直到删除相应的左括号。将每个运算符附加到 输出列表的末尾。 如果标记是运算符, *,/,+ 或 - ,将其压入 opstack。但是,首先删除已经在 opstack 中具有更高或相等优先级的任何运算符,并将它们加到输出列表中。
4.当输入表达式被完全处理时,检查 opstack。仍然在栈上的任何运算符都可以删除并加到 输出列表的末尾。
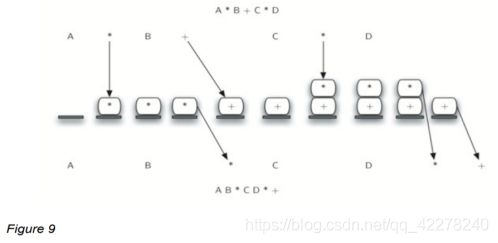
Figure 9 展示了对表达式 A * B + C * D 的转换算法。注意,第一个 * 在看到 + 运算符时被删除。另外,当第二个 * 出现时, + 保留在栈中,因为乘法优先级高于加法。在中缀表达式的末尾,栈被弹出两次,删除两个运算符,并将 + 作为后缀表达式中的最后一个运算符。
为了在 Python 中编写算法,我们使用一个名为 prec的字典来保存操作符的优先级。这个字典将每个运算符映射到一个整数,可以与其他运算符的优先级(我们使用整数3,2和1)进行比较。左括号将赋予最低的值。这样,与其进行比较的任何运算符将具有更高的优先级,将被放置在它的顶部。第15行将操作数定义为任何大写字符或数字。
from pythonds.basic.stack import Stack
def infixToPostfix(infixexpr):
prec = {}
prec["*"] = 3
prec["/"] = 3
prec["+"] = 2
prec["-"] = 2
prec["("] = 1
opStack = Stack()
postfixList = []
tokenList = infixexpr.split()
for token in tokenList:
if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
postfixList.append(token)
elif token == '(':
opStack.push(token)
elif token == ')':
topToken = opStack.pop()
while topToken != '(':
postfixList.append(topToken)
topToken = opStack.pop()
else:
while (not opStack.isEmpty()) and (prec[opStack.peek()] >= prec[token]):
postfixList.append(opStack.pop())
opStack.push(token)
while not opStack.isEmpty():
postfixList.append(opStack.pop())
return " ".join(postfixList)
print(infixToPostfix("A * B + C * D"))
print(infixToPostfix("( A + B ) * C - ( D - E ) * ( F + G )"))- 后缀表达式求值
考虑后缀表达式 4 5 6 * +
首先遇到操作数 4 和 5 ,此时,你还不确定如何处理它们,直到看到下一个符号。将它们放置到栈上,确保它们在下一个操作符出现时可用。
Figure 11 是个稍微复杂的示例, 7 8 + 3 2 + / 。在这个例子中有两点需要注意,首先,栈的大小增长收缩,然后在子表达式求值的时候再次增长。第二,除法操作需要谨慎处理。回想下,后缀表达式的操作符顺序没变,仅仅改变操作符的位置。当用于除法的操作符从栈中弹出时,它们被反转。由于除法不是交换运算符,换句话说 15/5 和 5/15 不同,因此我们必须保证操作数的顺序不会交换。
假设后缀表达式是一个由空格分隔的标记字符串。运算符为 *,/,+ 和 - ,操作数假定为单个整数值。输出将是一个整数结果。
- 创建一个名为operandStack 的空栈。
- 拆分字符串转换为标记列表。
- 从左到右扫描标记列表。如果标记是操作数,将其从字符串转换为整数,并将值压到operandStack。如果标记是运算符 *,/,+或 - ,它将需要两个操作数。弹出operandStack两次。 第一个弹出的是第二个操作数,第二个弹出的是第一个操作数。执行算术运算后,将结果压到操作数栈中。
- 当输入的表达式被完全处理后,结果就在栈上,弹出 operandStack 并返回值。
def postfixEval(postfixExpr):
operandStack = Stack()
tokenList = postfixExpr.split()
for token in tokenList:
if token in "0123456789":
operandStack.push(int(token))
else:
operand2 = operandStack.pop()
operand1 = operandStack.pop()
result = doMath(token,operand1,operand2)
operandStack.push(result)
return operandStack.pop()
def doMath(op, op1, op2):
if op == "*":
return op1 * op2
elif op == "/":
return op1 / op2
elif op == "+":
return op1 + op2
else:
return op1 - op2
print(postfixEval('4 4 + 0 2 + /'))