二叉树 (Binary Tree)的遍历

树是一种比较重要的数据结构，尤其是二叉树。二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

二叉树节点定义：

#define ElementType char
typedef struct Node {
    ElementType data;
    struct Node *lchild;
    struct Node *rchild;
}BinaryTree;

一、二叉树遍历递归遍历算法

1.先序遍历递归遍历算法

/*
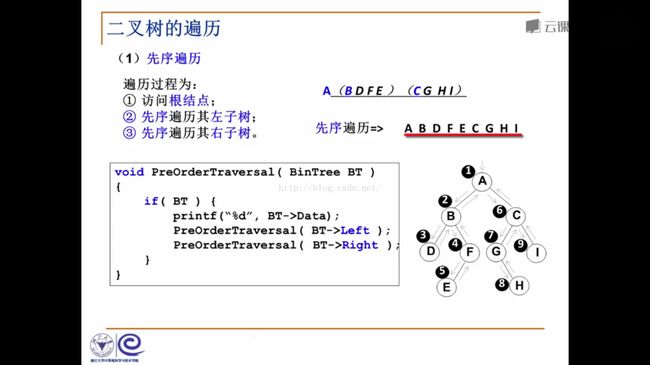
 (1)先序遍历 递归解法
 遍历过程为：
    1.访问根节点
    2.遍历其左子树
    3.遍历其右子树
*/
void PreOrderTraversal(BinaryTree* BT) {
    if (BT) {
        printf("%c", BT->data);
        PreOrderTraversal(BT->lchild);
        PreOrderTraversal(BT->rchild);
    }
}

2.中序遍历递归遍历算法

/*
 (2)中序遍历 递归解法
 遍历过程：
    1.遍历其左子树
    2.访问根节点
    3.遍历其右子树
*/
void InOrderTraversal(BinaryTree* BT) {
    if (BT) {
        InOrderTraversal(BT->lchild);
        printf("%c", BT->data);
        InOrderTraversal(BT->rchild);
    }
}

3.后序遍历递归遍历算法

/*
 (3)后序遍历 递归解法
 遍历过程：
    1.遍历其左子树
    2.遍历其右子树
    3.访问根节点
*/
void PostOrderTraversal(BinaryTree* BT) {
    if (BT) {
        PostOrderTraversal(BT->lchild);
        PostOrderTraversal(BT->rchild);
        printf("%c", BT->data);
    }
}

验证如下：

#include 
#include 

#define ElementType char
typedef struct Node {
    ElementType data;
    struct Node *lchild;
    struct Node *rchild;
}BinaryTree;

//创建二叉树节点
BinaryTree* CreateBinaryTree(data) {
    BinaryTree* t = (BinaryTree*)malloc(sizeof(BinaryTree));
    if (!t) {
        printf("空间不足！\n");
        return NULL;
    }
    t->lchild = NULL;
    t->rchild = NULL;
    t->data = data;
    return t;
}

/*
 (1)先序遍历 递归解法
 遍历过程为：
    1.访问根节点
    2.遍历其左子树
    3.遍历其右子树
*/
void PreOrderTraversal(BinaryTree* BT) {
    if (BT) {
        printf("%c", BT->data);
        PreOrderTraversal(BT->lchild);
        PreOrderTraversal(BT->rchild);
    }
}

/*
 (2)中序遍历 递归解法
 遍历过程：
    1.遍历其左子树
    2.访问根节点
    3.遍历其右子树
*/
void InOrderTraversal(BinaryTree* BT) {
    if (BT) {
        InOrderTraversal(BT->lchild);
        printf("%c", BT->data);
        InOrderTraversal(BT->rchild);
    }
}

/*
 (3)后序遍历 递归解法
 遍历过程：
    1.遍历其左子树
    2.遍历其右子树
    3.访问根节点
*/
void PostOrderTraversal(BinaryTree* BT) {
    if (BT) {
        PostOrderTraversal(BT->lchild);
        PostOrderTraversal(BT->rchild);
        printf("%c", BT->data);
    }
}

int main(int argc, const char * argv[]) {
    BinaryTree* tree_A = CreateBinaryTree('A');
    
    BinaryTree* tree_B = CreateBinaryTree('B');
    tree_A->lchild = tree_B;
    
    BinaryTree* tree_C = CreateBinaryTree('C');
    tree_A->rchild = tree_C;
    
    BinaryTree* tree_D = CreateBinaryTree('D');
    tree_B->lchild = tree_D;
    
    BinaryTree* tree_F = CreateBinaryTree('F');
    tree_B->rchild = tree_F;
    
    BinaryTree* tree_E = CreateBinaryTree('E');
    tree_F->lchild = tree_E;
    
    BinaryTree* tree_G = CreateBinaryTree('G');
    tree_C->lchild = tree_G;
    
    BinaryTree* tree_I = CreateBinaryTree('I');
    tree_C->rchild = tree_I;
    
    BinaryTree* tree_H = CreateBinaryTree('H');
    tree_G->rchild = tree_H;
    
    //先序遍历 => A B D F E C G H I
    PreOrderTraversal(tree_A);
    
    printf("\n");
    
    //中序遍历 => D B E F A G H C I
    InOrderTraversal(tree_A);
    
    printf("\n");
    
    //后序遍历 => D E F B H G I C A
    PostOrderTraversal(tree_A);
    
    return 0;
}

二、二叉树遍历非递归遍历算法

非递归算法实现的基本思路：使用栈

1.遇到一个节点，就把它压栈，并去遍历它的左子树。

2.当左子树遍历结束后，从栈顶弹出这个节点并访问它。

3.然后按其右指针再去遍历该节点的右子树。

#include 
#include 

#define ElementType char
typedef struct Node {
    int isFirst;
    ElementType data;
    struct Node *lchild;
    struct Node *rchild;
}BinaryTree;

typedef struct StackNode {
    BinaryTree* data;
    struct StackNode* next;
}Stack;
//初始化堆栈
Stack* CreateStack() {
    Stack* s;
    s = (Stack*)malloc(sizeof(Stack));
    if (!s) {
        printf("空间不足\n");
    }
    s->next = NULL;
    return s;
}
int IsEmpty(Stack* s) {
    return (s->next == NULL);
}
//入栈
void Push(Stack* s, BinaryTree* data) {
    Stack* cell;
    cell = (Stack*)malloc(sizeof(Stack));
    if (!cell) {
        printf("空间不足\n");
    }
    cell->data = data;
    cell->next = s->next;
    s->next = cell;
}
//出栈
BinaryTree* Pop(Stack* s) {
    Stack* firstCell;
    BinaryTree* topData;
    if (IsEmpty(s)) {
        printf("空栈\n");
        return NULL;
    }
    firstCell = s->next;
    s->next = firstCell->next;
    topData = firstCell->data;
    free(firstCell);
    return topData;
}


//创建二叉树节点
BinaryTree* CreateBinaryTree(data) {
    BinaryTree* t = (BinaryTree*)malloc(sizeof(BinaryTree));
    if (!t) {
        printf("空间不足！\n");
        return NULL;
    }
    t->lchild = NULL;
    t->rchild = NULL;
    t->data = data;
    return t;
}

//先序遍历非递归遍历解法
void PreOrderTraversal(BinaryTree* BT) {
    BinaryTree* T = BT;
    Stack* s = CreateStack(); //创建并初始化栈s
    while (T || !IsEmpty(s)) {
        while (T) { //一直向左并将沿途节点压入栈
            Push(s, T);
            printf("%c", T->data);
            T = T->lchild;
        }
        if (!IsEmpty(s)) {
            T = Pop(s); //节点弹出栈
            T = T->rchild; //转向右子树
        }
    }
}

//中序遍历非递归遍历解法
void InOrderTraversal(BinaryTree* BT) {
    BinaryTree* T = BT;
    Stack* s = CreateStack(); //创建并初始化栈s
    while (T || !IsEmpty(s)) {
        while (T) { //一直向左并将沿途节点压入栈
            Push(s, T);
            T = T->lchild;
        }
        if (!IsEmpty(s)) {
            T = Pop(s); //节点弹出栈
            printf("%c", T->data);
            T = T->rchild; //转向右子树
        }
    }
}

//后序遍历非递归遍历解法
void PostOrderTraversal(BinaryTree* BT) {
    BinaryTree* T = BT;
    Stack* s = CreateStack(); //创建并初始化栈s
    while (T || !IsEmpty(s)) {
        while (T) { //一直向左并将沿途节点压入栈
            T->isFirst = 1;
            Push(s, T);
            T = T->lchild;
        }
        if (!IsEmpty(s)) {
            T = Pop(s); //节点弹出栈
            if(T->isFirst == 1) { //表示是第一次出现在栈顶
                T->isFirst = 0;
                Push(s, T);
                T = T->rchild;
            }
            else { //第二次出现在栈顶
                printf("%c", T->data);
                T = NULL;
            }
        }
    }
}

int main(int argc, const char * argv[]) {
    BinaryTree* tree_A = CreateBinaryTree('A');
    
    BinaryTree* tree_B = CreateBinaryTree('B');
    tree_A->lchild = tree_B;
    
    BinaryTree* tree_C = CreateBinaryTree('C');
    tree_A->rchild = tree_C;
    
    BinaryTree* tree_D = CreateBinaryTree('D');
    tree_B->lchild = tree_D;
    
    BinaryTree* tree_F = CreateBinaryTree('F');
    tree_B->rchild = tree_F;
    
    BinaryTree* tree_E = CreateBinaryTree('E');
    tree_F->lchild = tree_E;
    
    BinaryTree* tree_G = CreateBinaryTree('G');
    tree_C->lchild = tree_G;
    
    BinaryTree* tree_I = CreateBinaryTree('I');
    tree_C->rchild = tree_I;
    
    BinaryTree* tree_H = CreateBinaryTree('H');
    tree_G->rchild = tree_H;
    
    printf("先序遍历非递归遍历算法：");
    //先序遍历 => A B D F E C G H I
    PreOrderTraversal(tree_A);
    
    printf("\n中序遍历非递归遍历算法：");
    //中序遍历 => D B E F A G H C I
    InOrderTraversal(tree_A);
    
    printf("\n后序遍历非递归遍历算法：");
    //后序遍历 => D E F B H G I C A
    PostOrderTraversal(tree_A);
    
    return 0;
}