详解Transformer (Attention Is All You Need)
文章目录
- 前言
- 1. Transformer 详解
-
- 1.1 高层Transformer
- 1.2 输入编码
- 1.3 Self-Attention
- 1.3 Multi-Head Attention
- 1.4 Encoder-Decoder Attention
- 1.5 损失层
- 2. 位置编码
- 3. 总结
转载来源:https://zhuanlan.zhihu.com/p/48508221
前言
注意力(Attention)机制由Bengio团队与2014年提出并在近年广泛的应用在深度学习中的各个领域,例如在计算机视觉方向用于捕捉图像上的感受野,或者NLP中用于定位关键token或者特征。谷歌团队近期提出的用于生成词向量的BERT算法在NLP的11项任务中取得了效果的大幅提升,堪称2018年深度学习领域最振奋人心的消息。而BERT算法的最重要的部分便是本文中提出的Transformer的概念。
正如论文的题目所说的,Transformer中抛弃了传统的CNN和RNN,整个网络结构完全是由Attention机制组成。更准确地讲,Transformer由且仅由self-Attenion和Feed Forward Neural Network组成。一个基于Transformer的可训练的神经网络可以通过堆叠Transformer的形式进行搭建,作者的实验是通过搭建编码器和解码器各6层,总共12层的Encoder-Decoder,并在机器翻译中取得了BLEU值得新高。
作者采用Attention机制的原因是考虑到RNN(或者LSTM,GRU等)的计算限制为是顺序的,也就是说RNN相关算法只能从左向右依次计算或者从右向左依次计算,这种机制带来了两个问题:
- 时间片 t t t 的计算依赖 t − 1 t-1 t−1 时刻的计算结果,这样限制了模型的并行能力;
- 顺序计算的过程中信息会丢失,尽管LSTM等门机制的结构一定程度上缓解了长期依赖的问题,但是对于特别长期的依赖现象,LSTM依旧无能为力。
Transformer的提出解决了上面两个问题,首先它使用了Attention机制,将序列中的任意两个位置之间的距离是缩小为一个常量;其次它不是类似RNN的顺序结构,因此具有更好的并行性,符合现有的GPU框架。论文中给出Transformer的定义是:Transformer is the first transduction model relying entirely on self-attention to compute representations of its input and output without using sequence aligned RNNs or convolution。
遗憾的是,作者的论文比较难懂,尤其是Transformer的结构细节和实现方式并没有解释清楚。尤其是论文中的 Q Q Q , V V V, K K K 究竟代表什么意思作者并没有说明。通过查阅资料,发现了一篇非常优秀的讲解Transformer的技术博客。本文中的大量插图也会从该博客中截取。首先感谢Jay Alammer详细的讲解,其次推荐大家去阅读原汁原味的文章。
1. Transformer 详解
1.1 高层Transformer
论文中的验证Transformer的实验室基于机器翻译的,下面我们就以机器翻译为例子详细剖析Transformer的结构,在机器翻译中,Transformer可概括为如图1:

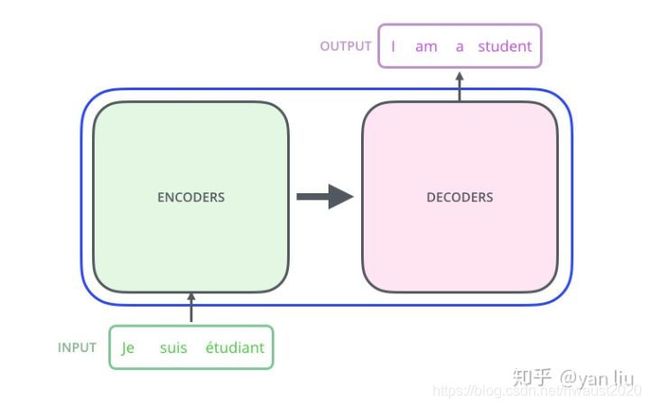
Transformer的本质上是一个Encoder-Decoder的结构,那么图1可以表示为图2的结构:
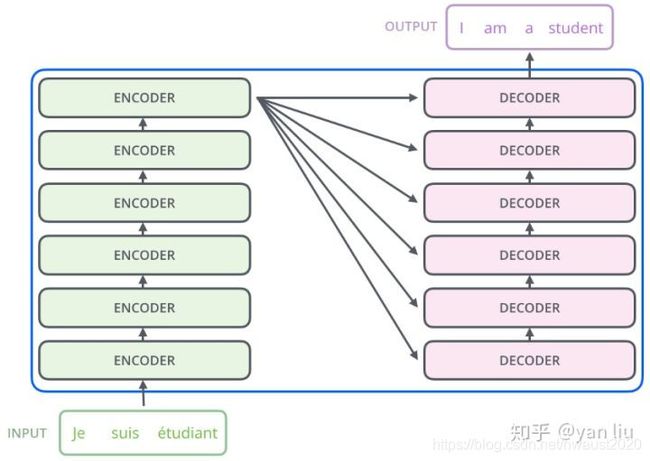
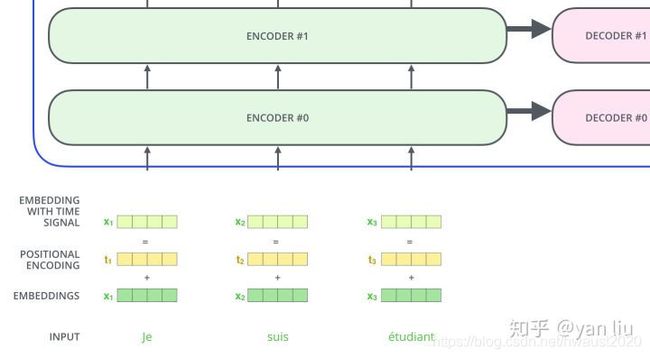
如论文中所设置的,编码器由6个编码block组成,同样解码器是6个解码block组成。与所有的生成模型相同的是,编码器的输出会作为解码器的输入,如图3所示:
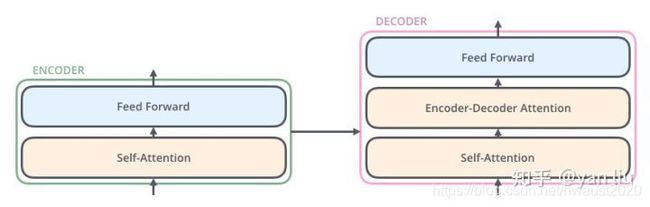
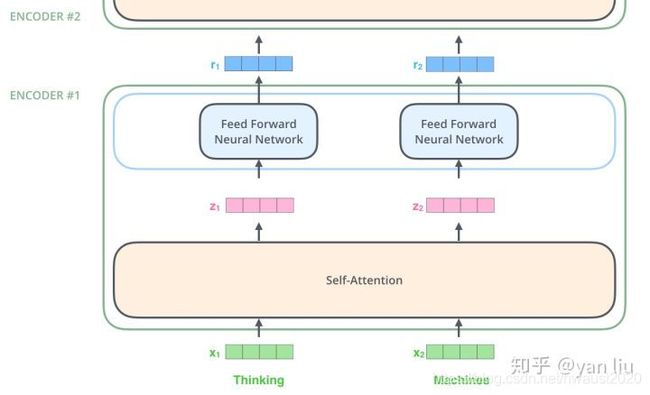
我们继续分析每个encoder的详细结构:在Transformer的encoder中,数据首先会经过一个叫做‘self-attention’的模块得到一个加权之后的特征向量 Z Z Z,这个 Z Z Z 便是论文公式1中的 A t t e n t i o n ( Q , K , V ) Attention(Q,K,V) Attention(Q,K,V):
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text { Attention }(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V Attention (Q,K,V)=softmax(dkQKT)V
第一次看到这个公式你可能会一头雾水,在后面的文章中我们会揭开这个公式背后的实际含义,在这一段暂时将其叫做 Z Z Z 。
得到 Z Z Z 之后,它会被送到encoder的下一个模块,即Feed Forward Neural Network。这个全连接有两层,第一层的激活函数是ReLU,第二层是一个线性激活函数,可以表示为:
FFN ( Z ) = max ( 0 , Z W 1 + b 1 ) W 2 + b 2 \operatorname{FFN}(Z)=\max \left(0, Z W_{1}+b_{1}\right) W_{2}+b_{2} FFN(Z)=max(0,ZW1+b1)W2+b2
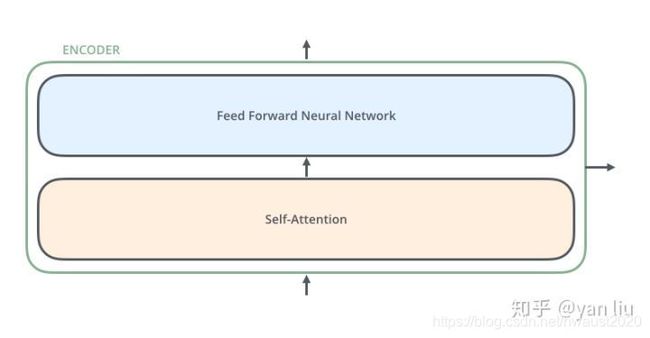
Encoder的结构如图4所示:
Decoder的结构如图5所示,它和encoder的不同之处在于Decoder多了一个Encoder-Decoder Attention,两个Attention分别用于计算输入和输出的权值:
1.2 输入编码
1.1节介绍的就是Transformer的主要框架,下面我们将介绍它的输入数据。如图6所示,首先通过Word2Vec等词嵌入方法将输入语料转化成特征向量,论文中使用的词嵌入的维度为 d m o d e l = 512 d_{model}=512 dmodel=512 。

在最底层的block中, x x x 将直接作为Transformer的输入,而在其他层中,输入则是上一个block的输出。为了画图更简单,我们使用更简单的例子来表示接下来的过程,如图7所示:
1.3 Self-Attention
Self-Attention是Transformer最核心的内容,然而作者并没有详细讲解,下面我们来补充一下作者遗漏的地方。回想Bahdanau等人提出的用Attention,其核心内容是为输入向量的每个单词学习一个权重,例如在下面的例子中我们判断it代指的内容,
The animal didn't cross the street because it was too tired
通过加权之后可以得到类似图8的加权情况,在讲解self-attention的时候我们也会使用图8类似的表示方式

在self-attention中,每个单词有3个不同的向量,它们分别是Query向量( Q Q Q),Key向量( K K K )和Value向量( V V V ),长度均是64。它们是通过3个不同的权值矩阵由嵌入向量 X X X 乘以三个不同的权值矩阵 W Q W^{Q} WQ , W K W^{K} WK , W V W^{V} WV 得到,其中三个矩阵的尺寸也是相同的。均是 512 × 64 512 \times 64 512×64。

那么Query,Key,Value是什么意思呢?它们在Attention的计算中扮演着什么角色呢?我们先看一下Attention的计算方法,整个过程可以分成7步:
- 如上文,将输入单词转化成嵌入向量;
- 根据嵌入向量得到 q , k , v q,k,v q,k,v三个向量;
- 为每个向量计算一个score: score = q ⋅ k =q \cdot k =q⋅k ;
- 为了梯度的稳定,Transformer使用了score归一化,即除以 d k \sqrt{d_{k}} dk ;
- 对score施以softmax激活函数;
- softmax点乘Value值 v v v ,得到加权的每个输入向量的评分 v v v ;
- 相加之后得到最终的输出结果 Z Z Z : z = ∑ v z=\sum v z=∑v。
上面步骤的可以表示为图10的形式。
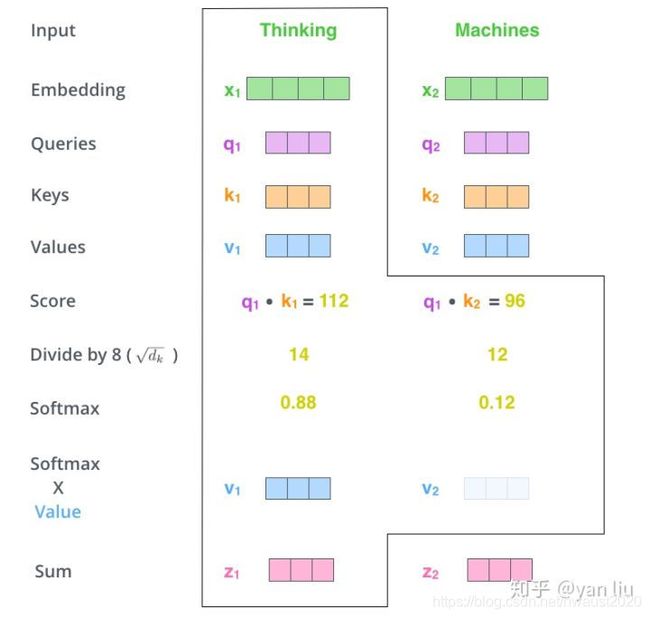
实际计算过程中是采用基于矩阵的计算方式,那么论文中的 Q , V , K Q,V,K Q,V,K 的计算方式如图11:

图10总结为如图12所示的矩阵形式:

这里也就是公式1的计算方式。
在self-attention需要强调的最后一点是其采用了残差网络 中的short-cut结构,目的当然是解决深度学习中的退化问题,得到的最终结果如图13。

1.3 Multi-Head Attention
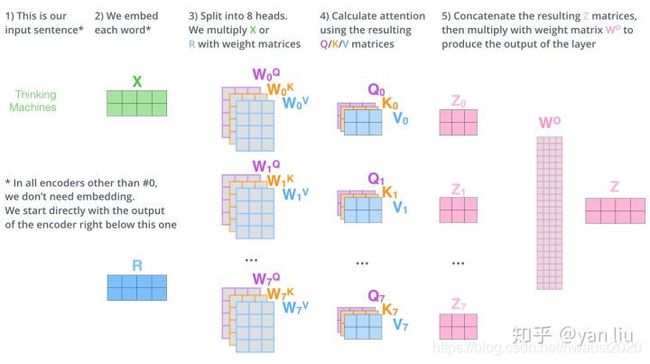
Multi-Head Attention相当于 h h h 个不同的self-attention的集成(ensemble),在这里我们以 h = 8 h=8 h=8举例说明。Multi-Head Attention的输出分成3步:
- 将数据 X X X 分别输入到图13所示的8个self-attention中,得到8个加权后的特征矩阵 Z i , i ∈ { 1 , 2 , … , 8 } Z_{i}, i \in\{1,2, \ldots, 8\} Zi,i∈{ 1,2,…,8} 。
- 将8个 Z i Z_{i} Zi 按列拼成一个大的特征矩阵;
- 特征矩阵经过一层全连接后得到输出 Z Z Z 。
整个过程如图14所示:
同self-attention一样,multi-head attention也加入了short-cut机制。
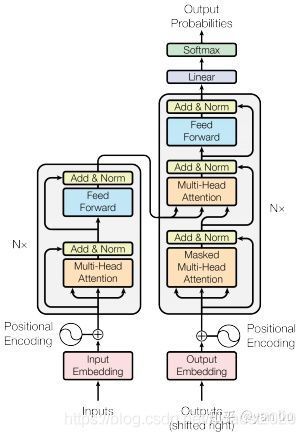
1.4 Encoder-Decoder Attention
在解码器中,Transformer block比编码器中多了个encoder-cecoder attention。在encoder-decoder attention中, Q Q Q 来之与解码器的上一个输出, K K K和 V V V则来自于与编码器的输出。其计算方式完全和图10的过程相同。
由于在机器翻译中,解码过程是一个顺序操作的过程,也就是当解码第 k k k 个特征向量时,我们只能看到第 k − 1 k-1 k−1 及其之前的解码结果,论文中把这种情况下的multi-head attention叫做masked multi-head attention。
1.5 损失层
解码器解码之后,解码的特征向量经过一层激活函数为softmax的全连接层之后得到反映每个单词概率的输出向量。此时我们便可以通过CTC等损失函数训练模型了。
而一个完整可训练的网络结构便是encoder和decoder的堆叠(各 N N N个, N = 6 N=6 N=6),我们可以得到图15中的完整的Transformer的结构(即论文中的图1):
2. 位置编码
截止目前为止,我们介绍的Transformer模型并没有捕捉顺序序列的能力,也就是说无论句子的结构怎么打乱,Transformer都会得到类似的结果。换句话说,Transformer只是一个功能更强大的词袋模型而已。
为了解决这个问题,论文中在编码词向量时引入了位置编码(Position Embedding)的特征。具体地说,位置编码会在词向量中加入了单词的位置信息,这样Transformer就能区分不同位置的单词了。
那么怎么编码这个位置信息呢?常见的模式有:a. 根据数据学习;b. 自己设计编码规则。在这里作者采用了第二种方式。那么这个位置编码该是什么样子呢?通常位置编码是一个长度为 d m o d e l d_{model} dmodel 的特征向量,这样便于和词向量进行单位加的操作,如图16。
论文给出的编码公式如下:
P E ( p o s , 2 i ) = sin ( p o s 1000 0 2 i d m o d e l ) P E(p o s, 2 i)=\sin \left(\frac{p o s}{10000^{\frac{2 i}{d_{m o d e l}}}}\right) PE(pos,2i)=sin(10000dmodel2ipos)
P E ( pos , 2 i + 1 ) = cos ( pos 1000 0 2 i d model ) P E(\text {pos}, 2 i+1)=\cos \left(\frac{\text {pos}}{10000^{\frac{2 i}{d_{\text {model}}}}}\right) PE(pos,2i+1)=cos(10000dmodel2ipos)
在上式中, p o s pos pos 表示单词的位置, i i i 表示单词的维度。关于位置编码的实现可在Google开源的算法中get_timing_signal_1d()函数找到对应的代码。
作者这么设计的原因是考虑到在NLP任务重,除了单词的绝对位置,单词的相对位置也非常重要。根据公式 sin ( α + β ) = sin α cos β + cos α sin β \sin (\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta sin(α+β)=sinαcosβ+cosαsinβ以及 cos ( α + β ) = cos α cos β − sin α sin β \cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta cos(α+β)=cosαcosβ−sinαsinβ ,这表明位置 k + p k+p k+p 的位置向量可以表示为位置 k k k 的特征向量的线性变化,这为模型捕捉单词之间的相对位置关系提供了非常大的便利。
3. 总结
优点:
- 虽然Transformer最终也没有逃脱传统学习的套路,Transformer也只是一个全连接(或者是一维卷积)加Attention的结合体。但是其设计已经足够有创新,因为其抛弃了在NLP中最根本的RNN或者CNN并且取得了非常不错的效果,算法的设计非常精彩,值得每个深度学习的相关人员仔细研究和品位。
- Transformer的设计最大的带来性能提升的关键是将任意两个单词的距离是1,这对解决NLP中棘手的长期依赖问题是非常有效的。
- Transformer不仅仅可以应用在NLP的机器翻译领域,甚至可以不局限于NLP领域,是非常有科研潜力的一个方向。
- 算法的并行性非常好,符合目前的硬件(主要指GPU)环境。
缺点:
- 粗暴的抛弃RNN和CNN虽然非常炫技,但是它也使模型丧失了捕捉局部特征的能力,RNN + CNN + Transformer的结合可能会带来更好的效果。
- Transformer失去的位置信息其实在NLP中非常重要,而论文中在特征向量中加入Position Embedding也只是一个权宜之计,并没有改变Transformer结构上的固有缺陷。