LeetCode-矩阵中最大矩形 Maximal Rectangle(python)
题目:在一个M * N的矩阵中,所有的元素只有0和1, 找出只包含1的最大矩形。
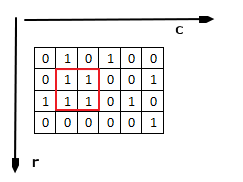
例如:图中是一个4 × 6的矩形,画出红色的是我们要找到的区域。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximal-rectangle/
查找最大矩形,所以它一定是以 某个行元素开始的,将要找到的某个矩形就转换成 一某一个行开始的最大矩形Histogram问题。
原始矩形可以变成如下的形式的数据:
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 2 | 1 | 0 | 0 | 1 |
| 1 | 3 | 2 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 |
Largest Rectangle in Histogram问题:
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/largest-rectangle-in-histogram/
![]()
两个方法:
方法一:
简单的,类似于 Container With Most Water,对每个柱子,左右扩展,直到碰到比自己矮的,计算这个矩
形的面积,用一个变量记录最大的面积,复杂度 O(n^2) ,会超时。
def largestRectangleArea(self, heights):
n = len(heights)
array = [x for x in heights] # 申请一个额外的数组
max_high = 0 # 最大面积
for i in range(1, n):
for j in range(i-1, -1, -1):
if array[j] > array[i]: # 数组arr里的元素,保持非递减的顺序。
if max_high < (i-j)*array[j]:
max_high = (i - j) * array[j]
array[j] = array[i]
else:
break
# 重新扫描一边,以更新最大面积
for i in range(n):
if array[i] * (n - i) > max_high:
max_high = array[i] * (n - i)
return max_high方法二:O(n)
如上图所示,从左到右处理直方,当 i=4 时,小于当前栈顶(即直方3),对于直方3,无论后面还是前面
的直方,都不可能得到比目前栈顶元素更高的高度了,处理掉直方3(计算从直方3到直方4之间的矩形的面
积,然后从栈里弹出);对于直方2也是如此;直到碰到比直方4更矮的直方1。
这就意味着,可以维护一个递增的栈,每次比较栈顶与当前元素。如果当前元素大于栈顶元素,则入栈,
否则合并现有栈,直至栈顶元素小于当前元素。结尾时入栈元素0,重复合并一次。
def largestRectangleArea(self, heights):
heights = [0] + heights + [0] # 添加左右两侧的特殊边界使得只有一个柱子时,也可以形成一个倒V型
lens = len(heights)
max_high = heights[0]
stack = []
for i in range(lens):
while stack and heights[i] < heights[stack[-1]]:
peek = stack.pop()
max_high = max((i - stack[-1] - 1) * heights[peek], max_high) # 对于stack[-1]来说其right_i=i,left_i=stack[-2]
stack.append(i)
return max_high接下回归正题:
一行一行求解 Largest Rectangle in Histogram问题,建立滚动数组heights []
def maximalRectangle(self, matrix: List[List[str]]) -> int:
if not matrix:
return 0
hights = [0] * len(matrix[0])
max_hight = 0
for i in range(0, len(matrix)):
for j in range(len(matrix[0])):
hights[j] = hights[j] + 1 if matrix[i][j] == "1" else 0
temp = self.find_largest_rectangle_area1(hights)
if temp > max_hight:
max_hight = temp
return max_hight其余栈的应用:
栈基本概念:https://blog.csdn.net/qq_19446965/article/details/102982047
接雨水:https://blog.csdn.net/qq_19446965/article/details/104144187
矩阵中最大矩形:https://blog.csdn.net/qq_19446965/article/details/82048028
基本计算器类:https://blog.csdn.net/qq_19446965/article/details/104717537
单调栈的应用:https://blog.csdn.net/qq_19446965/article/details/104720836