力扣解题思路:股票问题
121. 买卖股票的最佳时机
思路:这题为简单题,只要记录前面的最小价格,将这个最小价格作为买入价格,然后将当前的价格作为售出价格,查看当前收益是不是最大收益。
class Solution {
public int maxProfit(int[] prices) {
if(prices.length == 0) return 0;
int max = 0;
int min = prices[0];
for(int i=1;i<prices.length;i++){
if(min>prices[i]){
min = prices[i];
continue;
}
max = Math.max(max,prices[i]-min);
}
return max;
}
}122. 买卖股票的最佳时机 II
思路:为上一题的简单扩展,可以多次买卖,可以联想到贪心策略。当prices[i] - prices[i-1] > 0,那么就把 prices[i] - prices[i-1] 添加到收益中,这样的贪心策略是否是正确的呢?->
可以通过简单的证明:对于 [a, b, c, d],如果有 a <= b <= c <= d ,那么最大收益为 d - a。而 d - a = (d - c) + (c - b) + (b - a) ,因此当访问到一个 prices[i] 且 prices[i] - prices[i-1] > 0,那么就把 prices[i] - prices[i-1] 添加到收益中,这样的累计收益是最大的。
代码如下:
public int maxProfit(int[] prices) {
int profit = 0;
for (int i = 1; i < prices.length; i++) {
if (prices[i] > prices[i - 1]) {
profit += (prices[i] - prices[i - 1]);
}
}
return profit;
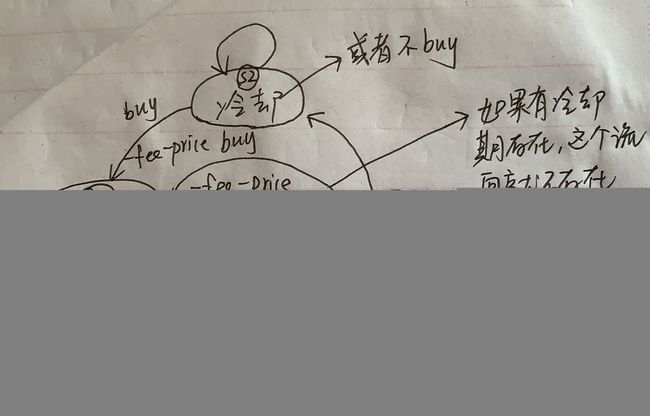
}首先有一点需要明确的是,s2和sell这两个状态是不持有股票的,而另外两个状态是持有股票的,按照这个状态转移图,我们定义四个动态规划数组,按照状态转移的方向更新动态方程即可。
注意,在状态的初始化时,若开始不持有股票则:
sell[0] = s2[0] = 0;若开始就持有股票则一定是当天买入的,此时:
s1[0] = buy[0] = -prices[0];完整代码:
public int maxProfit(int[] prices) {
if (prices == null || prices.length == 0) {
return 0;
}
int N = prices.length;
int[] buy = new int[N];
int[] s1 = new int[N];
int[] sell = new int[N];
int[] s2 = new int[N];
s1[0] = buy[0] = -prices[0];//不可以写Integer.MIN_VALUE,因为0不会再被更新而是从1开始更新,所以不可以参照空间优化的方式将其设置为Integer.MIN_VALUE
sell[0] = s2[0] = 0;
for (int i = 1; i < N; i++) {
buy[i] = s2[i - 1] - prices[i];
s1[i] = Math.max(buy[i - 1], s1[i - 1]);
sell[i] = Math.max(buy[i - 1], s1[i - 1]) + prices[i];
s2[i] = Math.max(s2[i - 1], sell[i - 1]);
}
return Math.max(sell[N - 1], s2[N - 1]);
}同样的,类似的有
714. 买卖股票的最佳时机含手续费
思路:同样可以参考上面的状态转移图,但是图中有个地方我标错了buy的时候是不用扣除手续费的,完整的代码如下:
public int maxProfit(int[] prices, int fee) {
int N = prices.length;
int[] buy = new int[N];
int[] s1 = new int[N];
int[] sell = new int[N];
int[] s2 = new int[N];
s1[0] = buy[0] = -prices[0];//不可以写Integer.MIN_VALUE,因为0不会再被更新而是从1开始更新,所以不可以参照空间优化的方式将其设置为Integer.MIN_VALUE
sell[0] = s2[0] = 0;
for (int i = 1; i < N; i++) {
buy[i] = Math.max(sell[i - 1], s2[i - 1]) - prices[i];
s1[i] = Math.max(buy[i - 1], s1[i - 1]);
sell[i] = Math.max(buy[i - 1], s1[i - 1]) - fee + prices[i];
s2[i] = Math.max(s2[i - 1], sell[i - 1]);
}
return Math.max(sell[N - 1], s2[N - 1]);
}修改、优化
虽然这两个题目的解法都通过了答案,但是我感觉是存在问题的,事实上并不应该存在四种状态,应该只有三种。所以我对上述状态提出改进,增加可读性:
对于 309. 最佳买卖股票时机含冷冻期 题 我们将状态分为三个,标记为0,1,2 分别表示不持有股票、持有股票、冷冻期:

这样就可以根据状态转移图写出动态方程了,不过这里我们就直接使用二维数组即可:
public int maxProfit(int[] prices) {
int len = prices.length;
// 特判
if (len < 2) {
return 0;
}
int[][] dp = new int[len][3];
// 初始化
dp[0][0] = 0;
dp[0][1] = -prices[0];
dp[0][2] = 0;
for (int i = 1; i < len; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][2] - prices[i]);
dp[i][2] = dp[i - 1][0];
}
return Math.max(dp[len - 1][0], dp[len - 1][2]);
}我感觉这样可读性也会强很多,然后看 714. 买卖股票的最佳时机含手续费 题:
每笔交易你只需要为支付一次手续费,没有冷冻期,我们仍然可以根据上面的新的状态转移图来写动态方程,不过这里的区别是只有两个状态,并且每次买入股票时都应该缴纳交易费用,初始化也是同样的方式。同样的,代码如下:
public int maxProfit(int[] prices, int fee) {
int n = prices.length;
int[][] dp = new int[n][2];
dp[0][0] = 0;
dp[0][1] = -prices[0]-fee;
for(int i=1;i<n;i++){
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i]-fee);
}
return dp[n-1][0];
}空间优化
当然,上面两种方式实际上都可以不用二维数组,用两个数来保存每个状态在每一轮的值就行啦~
public int maxProfit(int[] prices) {
int n = prices.length;
int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
int dp_pre_0 = 0; // 代表 dp[i-2][0]
for (int i = 0; i < n; i++) {
int temp = dp_i_0;
dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
dp_i_1 = Math.max(dp_i_1, dp_pre_0 - prices[i]);//这里不是dp_i_0,是因为冷却期的存在,不可能是在上次的基础上买入的,所以是在上上次的基础上买入的,所以应该是dp_pre_0
dp_pre_0 = temp;
}
return dp_i_0;
}
public int maxProfit_with_fee(int[] prices, int fee) {
int n = prices.length;
int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
for (int i = 0; i < n; i++) {
int temp = dp_i_0;
dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
dp_i_1 = Math.max(dp_i_1, temp - prices[i] - fee);
}
return dp_i_0;
}顺便提示一下,这个 Integer.MIN_VALUE 的设定也可以改成对应的-prices[i]或者-prices[i]-fee哦,效果是一样的哦~
(但是要注意没有空间优化的方法中的初始化中不可以写Integer.MIN_VALUE,因为0不会再被更新而是从1开始更新,所以不可以参照空间优化的方式将其设置为Integer.MIN_VALUE)
123. 买卖股票的最佳时机 III
思路:这一题限制交易的次数只有两次,所以我们直接用穷举法就好了,我们只需要定义四个变量:
fstBuy: 在该天第一次买入股票可获得的最大收益
fstSell: 在该天第一次卖出股票可获得的最大收益
secBuy: 在该天第二次买入股票可获得的最大收益
secSell: 在该天第二次卖出股票可获得的最大收益
遍历完数组后,我们只需要取最后一个secSell即为最终答案:
public int maxProfit(int[] prices) {
int fstBuy = Integer.MIN_VALUE, fstSell = 0;
int secBuy = Integer.MIN_VALUE, secSell = 0;
for(int p : prices) {
fstBuy = Math.max(fstBuy, -p);
fstSell = Math.max(fstSell, fstBuy + p);
secBuy = Math.max(secBuy, fstSell - p);
secSell = Math.max(secSell, secBuy + p);
}
return secSell;
}初始化也可以这样写:
if(prices.length == 0) return 0;
int fstBuy = -prices[0], fstSell = 0;
int secBuy = -prices[0], secSell = 0;因为第一次和第二次交易时有顺序的,所以也可以这么写比较清晰:
public int maxProfit(int[] prices) {
int firstBuy = Integer.MIN_VALUE, firstSell = 0;
int secondBuy = Integer.MIN_VALUE, secondSell = 0;
for (int curPrice : prices) {
if (firstBuy < -curPrice) {
firstBuy = -curPrice;
}
if (firstSell < firstBuy + curPrice) {
firstSell = firstBuy + curPrice;
}
if (secondBuy < firstSell - curPrice) {
secondBuy = firstSell - curPrice;
}
if (secondSell < secondBuy + curPrice) {
secondSell = secondBuy + curPrice;
}
}
return secondSell;
}188. 买卖股票的最佳时机 IV
思路:这一题可以说是上一题的扩展,只能进行 k 次的股票交易,当k == 2就是上一题了。在力扣上看了好多关于这一题的题解,很多都是用的三维动态规划数组,这个还是很容易想到的,那么问题在于如何更新这个k呢其实很多题解都给出了如何更新k,但是都没有说明原因,于是我参考了一个比较好理解的题解,戳这里o(▽)q
首先,我们定义 dp[i][j][K] :表示到第 i 天为止,已经交易了 j 次,并且当前持股状态为 K 的最大收益。其中K为0时表示不持股,为1时表示持股。接下来写状态转移方程:
dp[i][j][0] = max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]); (1)
dp[i][j][1] = max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]) (2)这里比较容易出错的一个地方是,我们只有每次买入的时候才需要将交易次数加一,卖出的时候则不需要加一,所以(2)式中买入时出现了 j-1 (这两个方程也是参考上面我所画的两状态的状态转移图写出来的,比较简单)。
接下来进行动态规划数组的初始化,所有不持股的状态值初始化的时候为 0。所有持股的状态值都设置为一个很大的负数(至少应该是最大的股价的负数-1),表示未知。这里i 和j 下标都有-1 ,所以i 和j 可以多设置一行,以避免复杂的分类讨论。我们这里就不多设置一行了,更新数组的时候需要从0开始更新而不是1:
for (int i = 0; i < len; i++) {
for (int j = 0; j < k; j++) {
dp[i][j][1] = -9999;
}
}还有一点,由于更新数组的时候需要从0开始,我们可以看出,(1)(2)式中都可能用到数组下标为-1的情况,这意味着我们在循环遍历i,j时需要进行相应的初始化:
for (int i = 0; i < len; i++) {
for (int j = 0; j < k; j++) {
if (i == 0) {
dp[i][j][1] = -prices[0];
dp[i][j][0] = 0;
} else {
if (j == 0) {
dp[i][j][1] = Math.max(dp[i - 1][j][1], -prices[i]);
} else {
// 基本状态转移方程 1
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
}
// 基本状态转移方程 2
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
}
}
}当k大于等于数组长度一半时, 问题退化为贪心问题此时采用 买卖股票的最佳机II
的贪心方法解决可以大幅提升时间性能, 对于其他的k, 可以采用 买卖股票的最佳时机 III的方法来解决:
public int greedy(int[] prices, int len) {
int res = 0;
for (int i = 1; i < len; i++) {
if (prices[i - 1] < prices[i]) {
res += prices[i] - prices[i - 1];
}
}
return res;
}最后返回dp[len - 1][k - 1][0]即可,因为i,j没有多设置一行,完整代码如下:
public int maxProfit(int k, int[] prices) {
int len = prices.length;
if (k == 0 || len < 2) {
return 0;
}
if (k >= len / 2) {
return greedy(prices, len);
}
int[][][] dp = new int[len][k][2];
for (int i = 0; i < len; i++) {
for (int j = 0; j < k; j++) {
dp[i][j][1] = -9999;
}
}
for (int i = 0; i < len; i++) {
for (int j = 0; j < k; j++) {
if (i == 0) {
dp[i][j][1] = -prices[0];
dp[i][j][0] = 0;
} else {
if (j == 0) {
dp[i][j][1] = Math.max(dp[i - 1][j][1], -prices[i]);
} else {
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
}
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
}
}
}
return dp[len - 1][k - 1][0];
}
public int greedy(int[] prices, int len) {
int res = 0;
for (int i = 1; i < len; i++) {
if (prices[i - 1] < prices[i]) {
res += prices[i] - prices[i - 1];
}
}
return res;
}按照先前的空间优化的原理,我们可以写出空间优化后的版本,即去掉第一维度:
public int maxProfit(int k, int[] prices) {
int len = prices.length;
if (k == 0 || len < 2) {
return 0;
}
if (k >= len / 2) {
return greedy(prices, len);
}
int[][] dp = new int[k][2];
for (int j = 0; j < k; j++) {
dp[j][1] = -9999;
}
for (int price : prices) {
for (int j = 0; j < k ; j++) {
if (j == 0) {
dp[j][1] = Math.max(dp[j][1], -price);
} else {
dp[j][1] = Math.max(dp[j][1], dp[j - 1][0] - price);
}
dp[j][0] = Math.max(dp[j][0], dp[j][1] + price);
}
}
return dp[k - 1][0];
}
public int greedy(int[] prices, int len) {
int res = 0;
for (int i = 1; i < len; i++) {
if (prices[i - 1] < prices[i]) {
res += prices[i] - prices[i - 1];
}
}
return res;
}当然两个状态也可以拆开表示,和上面其实是一样的:
public int maxProfit(int k, int[] prices) {
int len = prices.length;
if (len < 2 || k == 0) {
return 0;
}
if (k >= len / 2) {
return greedy(prices, len);
}
// k 次持股分别的状态
int[] stock = new int[k];
Arrays.fill(stock, -9999);
// k 次不持股(持有现金)分别的状态
int[] cash = new int[k];
for (int price : prices) {
for (int j = 0; j < k; j++) {
stock[j] = Math.max(stock[j], (j == 0 ? 0 : cash[j - 1]) - price);
cash[j] = Math.max(cash[j], stock[j] + price);
}
}
return cash[k - 1];
}