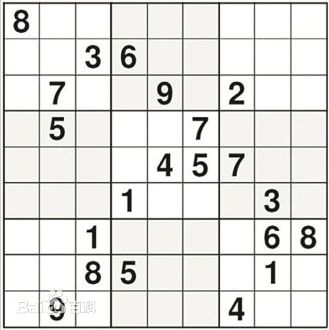
【算法分析】回溯法解数独（九宫格）算法

    这篇文章，是来详细介绍怎样写出一个算法，来解出所有的数独问题。算法的程序运行时间，缩减在了毫秒级别。等到这篇文章结束，我会抽时间写一篇文章，介绍如何生成一个随机的唯一解的数独问题。
    另外，为了做图形方便，示范代码是用C++，喜欢其他语言的朋友，可以参考一下思路。

数独，是源自18世纪瑞士的一种数学游戏。是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫（3*3）内的数字均含1-9，不重复。

数独盘面是个九宫，每一宫又分为九个小格。在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次，所以又称“九宫格”

利用算法解数独，主要采用了回溯法。思路如下：

1 .遍历已生成的数独二维数组，得出空白格子的数目。

2 .从第一个空白格子开始，利用数独的规范，对比同一列，同一行，以及同一个九宫格的数字，找出其所有可行解，存入数组（利用整形变量的位运算，会有更高的效率）。利用最后一个可行解，进行下一步运算。

3 .对剩下的格子进行同样的操作。

4 .如遇到无解的情况，则进行回溯操作。继续重复上述运算。

5 .当所有空白格子填满，所得结果，即为数独的解。

具体算法实现如下：

#include 
#include 
#include 


using namespace std;

#define MAX 9

typedef struct node
{
    int col;
    int row;
    int value[MAX+1];
}Node;

void print_sudoku(int Sudoku[MAX][MAX]);
int count_num_empty(int Sudoku[MAX][MAX]);
void backtrack(int Sudoku[MAX][MAX], int num_empty, Node *node_stack);
int findvalue(int Sudoku[MAX][MAX], Node *node_stack);



int findvalue(int Sudoku[MAX][MAX], Node *node_stack)
{
    int i = node_stack->col;
    int j = node_stack->row;
    int k = 0;
    int n = 0;

    for(k = 0; k < MAX+1; ++k)
        node_stack->value[k] = 0;

    for(k = 1; k < MAX+1; ++k)
    {
        node_stack->value[Sudoku[i][k-1]] = 1;
        node_stack->value[Sudoku[k-1][j]] = 1;
    }

    for(k = 0; k < 3; ++k)
    {
        for(n = 0; n < 3; ++n)
        {
            node_stack->value[Sudoku[i/3*3+k][j/3*3+n]] = 1;
        }
    }

    node_stack->value[0] = 0;

    for(k = 1; k < MAX+1; ++k)
        if(node_stack->value[k] == 0)
            node_stack->value[0]++;

    for(k = 1; k < MAX+1; ++k)
    {
        if(node_stack->value[k] == 0)
        {
            node_stack->value[k] = 1;
            node_stack->value[0]--;
            break;
        }
    }

    if(k == MAX+1)
        return -1;
    else
        return k;
}

void backtrack(int Sudoku[MAX][MAX], int num_empty, Node *node_stack)
{
    int i = 0;
    int j = 0;
    int k = 0;
    int flag = 0;
    while(num_empty)
    {
        for(i = 0; i < MAX; ++i)
        {
            for(j = 0; j < MAX; ++j)
            {
                if(Sudoku[i][j] == 0)
                {
                    (node_stack + k)->col = i;
                    (node_stack + k)->row = j;
                    Sudoku[i][j] = findvalue(Sudoku, node_stack + k);
                    if(Sudoku[i][j] == -1)
                    {
                        Sudoku[i][j] = 0;
                        k--;
                        while((node_stack + k) -> value[0] == 0)
                        {
                            if(k == 0)
                            {
                                cout << "数独无解" << endl;
                                exit(1);
                            }
                            Sudoku[(node_stack + k) -> col][(node_stack + k) -> row] = 0;
                            num_empty++;
                            k--;
                        }
                        for(flag = 1; flag < MAX+1; ++flag)
                        {
                            if((node_stack + k)->value[flag] == 0)
                            {
                                Sudoku[(node_stack + k) -> col][(node_stack + k) -> row] = flag;
                                (node_stack + k)->value[flag] = 1;
                                (node_stack + k)->value[0]--;
                                break;
                            }
                        }
                        num_empty++;
                        i = (node_stack + k)->col;
                        j = (node_stack + k)->row;
                    }
                    k++;
                    num_empty--;
                }
            }
        }
    }

    free(node_stack);
    node_stack = NULL;
    print_sudoku(Sudoku);
}


int count_num_empty(int Sudoku[MAX][MAX])
{
    int num = 0;
    for(int i = 0; i < MAX; ++i)
    {
        for(int j = 0; j < MAX; ++j)
        {
            if(Sudoku[i][j] == 0)
                num++;
        }
    }
    return num;
}

void print_sudoku(int Sudoku[MAX][MAX])
{
    for(int i = 0; i < MAX; ++i)
    {
        for(int j = 0; j < MAX; ++j)
        {
            cout << " " <int main(int argc, char const* argv[])
{

#if 0
    int Sudoku[MAX][MAX];

    for(int i = 0; i < MAX; ++i)
    {
        for(int j = 0; j < MAX; ++j)
        {
            cin >> Sudoku[i][j];
        }
    }
#endif

#if 1
    int Sudoku[MAX][MAX] = {
        (8,0,0,0,0,0,0,0,0),
        (0,0,3,6,0,0,0,0,0),
        (0,7,0,0,9,0,2,0,0),
        (0,5,0,0,0,7,0,0,0),
        (0,0,0,0,4,5,7,0,0),
        (0,0,0,1,0,0,0,3,0),
        (0,0,1,0,0,0,0,6,8),
        (0,0,8,5,0,0,0,1,0),
        (0,9,0,0,0,0,4,0,0)
    };
#endif
    int num_empty = count_num_empty(Sudoku);
    Node * node_stack = (Node *)malloc(sizeof(struct node) * num_empty);

    backtrack(Sudoku, num_empty, node_stack);

    return 0;
}

用C#写出图形之后的完整版本在github可以下载，感兴趣的朋友可以下载看看：
https://github.com/ShayWxy/Sudoku