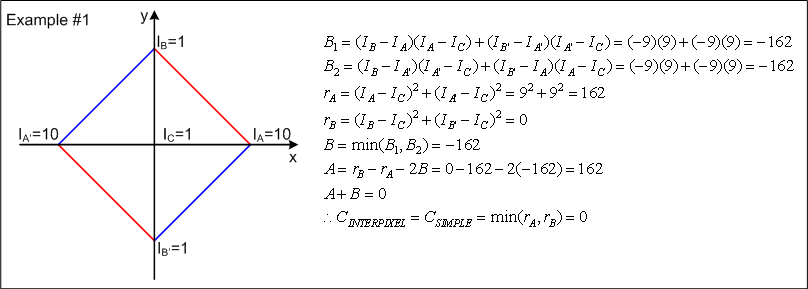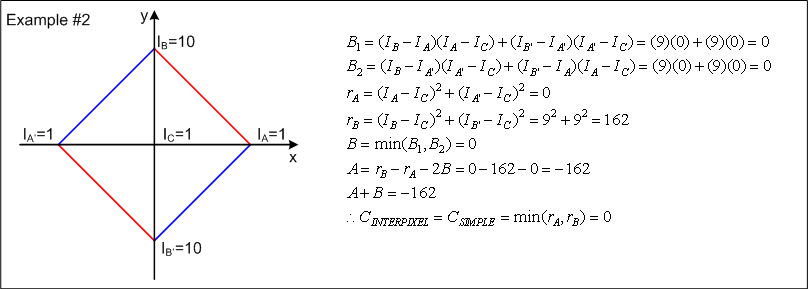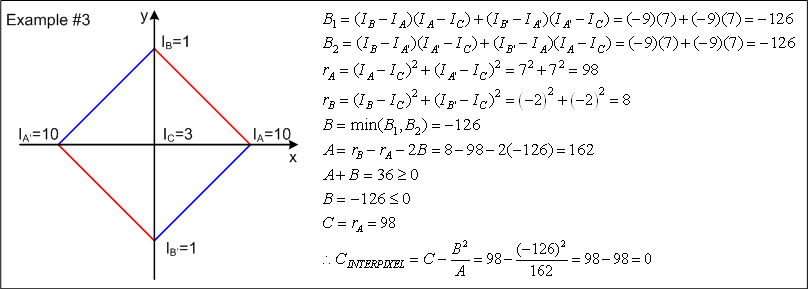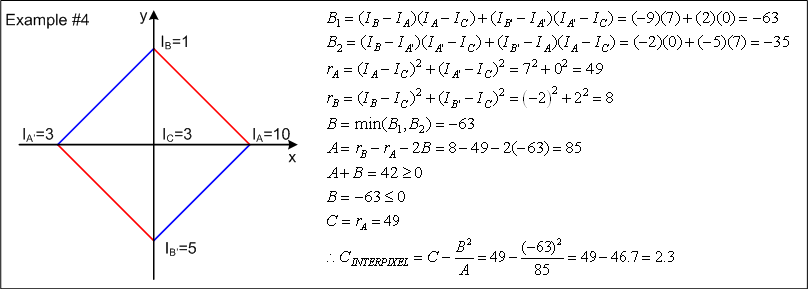图像角点检测之Trajkovic算子
背景引言
本节主要内容来源于是由 Miroslav Trajkovic和Mark Hedley[1]在1998年提出Trajkovic算子,其论文为FastCorner Detection.和Trajkovic Operator (4-Neighbours)[3](注:本节图片主要是来源于此)。Trajkovic算子角点提取方法存在价值是在角点提取的效果上,它优于同时期的其他角点(如Moravec角点,Harris角点)提取方法,同时,从算法的运行速度角度而言,它比同是期的其他角点提取方法要快很多。
基本理论
作者对角点的定义,与Moravec角点(关于Moravec角点检测,参考于博文Moravec角点检测)、 Harris 角点(关于Harris角点检测,参考于博文Harris角点检测)的定义是一样的:图像灰度值在各个方向变化都比较大的点,即认为是角点。角点量的定义也类似于Moravec,即角点量的是在各个方向上灰度变化的最小值(当在某个方向上,灰度值的变化最小,并且这个最小值也大于某某个设定的阈值,那么认为这个点就是一个角点)。与Moravec 相比 ,Trajkovic 的性能更好,因为Trajkovic通过使用像素插值的方法比较每一个方向上的灰度值变化程度,而moravec只有限个方向的比较,与harris相比,两都效果差不多,但是Trajkovic的速度远快于haris.
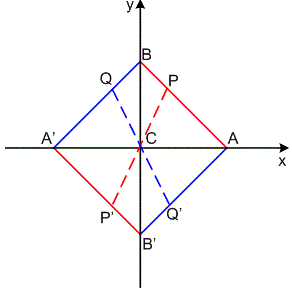
Trajkovic在速度方面的表现于决定它能够应用对实时要求比较高的系统中。但是Trajkovic也有缺点是它不具备旋转不变性,对噪声比较敏感,对对角点的响应值比较大等。对于这些缺点也会有相应的方法,但不能完全的解决这些缺点。Trajkovic算子计算角点量是在一个小的圆形窗口内,并且考虑了所有通过圆心的直线,即计算了每一个可能的方向上的灰度值变化程度)。假设用C表示圆的圆心,那么通过圆心C的任意一条直线会与圆在两个交点,如图1所示:
Figure 1: Notation for Trajkovic Operator
那么,Trajkovic对角点量的定义是
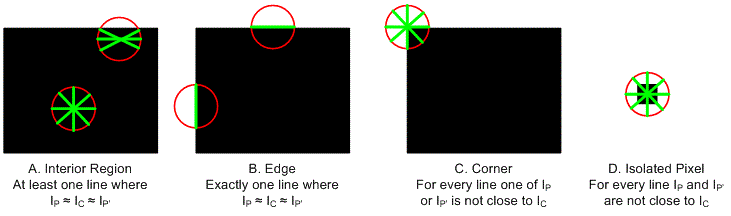
C(x,y)表示的是图像I上,任意一点(x,y)处的角点量。这个公式能断出是否是角点。点(x,y)在图像目的位置有四种情况。如下图所示:
第一情况:点(x,y)在内部区域:此时经点(x,y)位中心的圆形窗中完全在一个比较平坦的区域,或者大部分的圆形窗口是在这个平坦区域的(如上图A所示)。这种情况下,至少存大一条直线过中心点C的直线使得Ic约等于Ip和Ic约等于Ip‘,根据角点量计算公式,计算出的C(x,y)一定是一个很小的值,那么就可以排除点(x,y)不是角点。并且,大多数的情况下,会有多个这样的点P存大,使得对噪声一定的承受能力。
第二情况:点(x,y)在边缘上:此时圆形窗口的中心点(x,y)刚好落在边缘上(如上图B所示)。仅存在一个点对P,P'使得Ic约等于Ip和Ic约等于Ip‘。在理想状况下,根据角点量的公式计算出来的角点量C(x,y)是比较小的。但是由于只存在一个条这样直线,所以容易受到噪声的干扰。
第三情况:点(x,y)在角点上:当圆窗口的中心(x, y)位于角点上时(如上图C 所示)。任意一条通过点(x,y)与圆相交的交点P、P', P、P' 中至少有一个点的灰度值与中心的点的灰度值差别比较大。所以计算出来的角点量也比较大(大于设定的阈值,所以会被认为是角点)。
第四情况:点(x,y)在一个孤立点上:如果在孤立点上(如上图D所示),对于每一个直线上的Ip, Ip’,都分与Ic的值相差比较大,此时计算出的角点量也比较大。此时这个点是噪声,但是由于角点量比较大,会被认为是角点。为了削除这种噪声的影响,可以先使用高斯平滑进行去噪。
根据上面的分析,Trajkovic 受噪声的影响比较大,所以,可以先实现高斯平滑去噪再使用Trajkovic算子进行角点检测。
角点量的计算方法
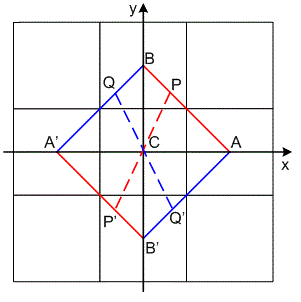
目前,关于Trajkovic计算角点量的并未具体介绍如何时计算。首先,如下图2所示,水平方向的灰度值变化量rA,垂直方向的灰度值变化量rB很容易计算。
如何计算任意一个方向上灰度值的变化程度呢?首先,我们角点量就取其最小值即可:
Figure 2: Interpixel positions Figure3: Interpixel approximation for a 3x3 window using 4-neighbours
现在,我们可将问题可以转换为,任意一条通过点C 的直线与圆的交点是P,P',Q,Q'即可:
把公式(2)代入公式(1) 中即可:
那么,![]() 最小值是即可结论是
最小值是即可结论是
现在我们理解上述公式,在此转载Trajkovic Operator Examples的例子。
==========下来例子来自Trajkovic Operator Examples====================================
Since IB=IB'=IC the minimum intensity variation is zero and corresponds to the line BB'.
Since IA=IA'=IC the minimum intensity variation is zero and corresponds to the line AA'.
Along the line AB there will be a point P where the intensity is 3. The line PC will intersect the line A'B' at P' where clearly the intensity will also be 3. Therefore, the minimum intensity variation is zero and corresponds to the line PP'.
Along the line AB there will be a point P where the intensity is 3. Point P occurs a distance (3-1)/(10-1)=2/9 along the line BA from point B. The line PC will intersect the line A'B' at P' a distance of 2/9 from B'. At a distance of 2/9 from B' the intensity is 5-(2/9)(5-3)=4.55. Therefore, the minimum intensity variation is around (4.55-3)2=2.42. As indicated by the results of example 4, there is in fact a line with a smaller intensity variation (intuitively, this will be at a point a slightly smaller distance along the line BA from point B).
====================================================
多格算法(Multigrid Algorithm)
角点可以分为两类:几何角点和纹理角点。几何角点是由图像中物体边缘的相交。而纹理角点有由物体表面的纹理产生的角点(如:草地,衣服的纹理等)。通常情况下,一幅图像中的几何角点的数量要远少于纹理角点。多格算法的目的是希望能多检测到几何角点,少检测到纹理点。因Trajkovic 认为几何角点比纹理角点更加的稳定。所以,从实践使用来看,减少纹理角点是合理的。
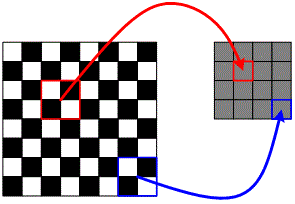
经过观察发现,纹理角点一般都是非常的密集,并且是在一个很小区域内灰度值发生变化,所以,采用把原图缩小以后,再来提取角点,通过缩小图像,可以消除区域内灰度值的变换。缩小图像的方法不是使用插值法,而是使用平均法。如下图所示:
Trajkovic角点检测,首先使用多格法对原如图像进行缩小,这样不仅能够减少检测到纹理角点数目,而且加快了Trajkovic角点检测的速度,在Trajkovic角点检测缩小版的图像上,使用角为简单的角点量计算公式初步判断是不是侯选角点。如果是,再到原始图像上进一步判定。
Figure 4: Corner points detected at different image resolutions
如图4所示,原始的大小是256*256,图像中有一片草地,而草地上的角点,对于我们进行角点匹配时,是没有什么意义。当把图像缩小到128*128时,草地上的角点已经消除了。当然,图像也不能缩小太多,否则,几何角点也会消失,当缩小到64*64时,部分几何角点也消失了。
算法流程
Trajkovic角点检测的算法如下所示:
现在,贴出给Trajkovic Operator函数代码,仅作参考.
参考代码
Trajkovic Operator(4-Neighbours)函数
CvSeq* CImgCorners::Tajkovic4Corners(IplImage *srcImg){
if(!srcImg){
printf("ERROR: Load File in Tajkovice4Corners(....)");
exit(EXIT_FAILURE);
}
IplImage* srcGray = cvCreateImage(cvGetSize(srcImg),8,1);
cvCvtColor(srcImg,srcGray,CV_BGR2GRAY);
IplImage* srcRes =cvCreateImage(cvSize(srcGray->width/2,srcGray->height/2),8,1);
CvMemStorage* mem = cvCreateMemStorage(0);
CvSeq* corners = cvCreateSeq(0,sizeof(CvSeq),sizeof(CvPoint),mem);
int scaleX = srcImg->width/srcRes->width;
int scaleY = srcImg->height/srcRes->height;
IplImage*srcResMap = cvCreateImage(cvGetSize(srcRes),8,1);
IplImage* srcMap = cvCreateImage(cvGetSize(srcImg),32,1);
int IC,IA,IB,IAA,IBB;
int rA,rB,C_Simple;
for(int y=1;yheight-1;y++){
uchar*preRow = (uchar*)(srcRes->imageData +(y-1)*srcRes->widthStep);
uchar*curRow = (uchar*)(srcRes->imageData + y*srcRes->widthStep);
uchar*nextRow =(uchar*)(srcRes->imageData+(y+1)*srcRes->widthStep);
uchar*MapData =(uchar*)(srcResMap->imageData+y*srcResMap->widthStep);
for(x=1;xwidth-1;x++){
IC = curRow[x]&0xFF;
IA = curRow[x+1]&0xFF;
IAA = curRow[x-1]&0xFF;
IB = preRow[x]&0xFF;
IBB = nextRow[x]&0xFF;
rA = (IA-IC)*(IA-IC) + (IAA-IC)*(IAA-IC);
rB = (IB-IC)*(IB-IC) + (IBB-IC)*(IBB-IC);
C_Simple = MaxData(rA, rB);
if(C_Simple > 200) MapData[x]=1;
}
}
for( y=1;yheight-1;y++){
uchar*srcResMapData =(uchar*)(srcResMap->imageData +
y*srcResMap->widthStep);
for(x=1;xwidth-1;x++){
if(srcResMapData[x]==0) continue;
uchar*srcPreRow =(uchar*)(srcImg->imageData+(y*scaleY-1)*srcImg->widthStep);
uchar*srcCurRow =(uchar*)(srcImg->imageData+y*scaleY*srcImg->widthStep);
uchar*srcNextRow=(uchar*)(srcImg->imageData+(y*scaleY+1)*srcImg->widthStep);
IC = srcCurRow[x*scaleX]&0xFF;
IA = srcCurRow[x*scaleX+1]&0xFF;
IAA = srcCurRow[x*scaleX-1]&0xFF;
IB = srcPreRow[x*scaleX]&0xFF;
IBB = srcNextRow[x*scaleX]&0xFF;
rA = (IA-IC)*(IA-IC) + (IAA-IC)*(IAA-IC);
rB = (IB-IC)*(IB-IC) + (IBB-IC)*(IBB-IC);
C_Simple = MaxData(rA, rB);
if(C_Simple>300) {
float B1,B2,A,B,C,C_InterPixel;
B1 = (IB-IA)*(IA-IC)+(IBB-IAA)*(IAA-IC);
B2 = (IB-IAA)*(IAA-IC)+(IBB-IA)*(IA-IC);
B = Maxdata(B1,B2);
A = rB-rA-2*B;
C = rA;
if(B<0 &&(A+B)>0) C_InterPixel = C-(B*B)/A;
else C_InterPixel=C_Simple;
if(C_InterPixel>300){
float*srcMapData=(float*)(srcMap->imageData+originY*srcMap->widthStep);
srcMapData[originX]=C_InterPixel;
}
}
}
}
int beginY= 4, beginX = 4;
int endY = srcMap->height - 4;
int endX = srcMap->width - 4;
float maxValue=0;
int flag = 0 ;
CvPoint maxLoc;
for(y=beginY;ymaxValue){
maxValue = value;
maxLoc.x = x+winx;
maxLoc.y = y+winy;
flag = 1;
}
}
}
if(flag==1 && maxValue>300) cvSeqPush(corners,&maxLoc);
x = x+4;
}
y = y + 4;
}
cvReleaseImage(&srcResMap);
cvReleaseImage(&srcMap);
cvReleaseMemStorage(&mem);
return corners;
} 测试输出
原始图像如下图所示:
经Trajkovic算子的提取的角点,如下图所示:
在博文【特征检测】Moravec检测器介绍了Moravec算子的提取的角点原理,在此时,给出测试输出结果与本节介绍Trajkovic算子的提取的角点进行直观比较。经Moravec算子的提取的角点,如下图所示:
在博文【特征检测】Harris检测器介绍了Harris算子的提取的角点原理,在此时,给出测试输出结果与本节介绍Trajkovic算子的提取的角点进行直观比较。经Harris算子的提取的角点,如下图所示:

参考文献
[1] M. Trajkovic and M. Hedley . "Fast corner detection".Image and Vision Computing 16 (2): 75–87,1998.
[2] Corner Detection From Wikipedia, the free encyclopedia.
[3] Trajkovic Operator (4-Neighbours).
关于Image Engineering & Computer Vision的更多讨论与交流,敬请关注本博和新浪微博songzi_tea.