分类变量回归——Probit和Logit（附代码）

为什么不是普通线性回归？

使用普通线性回归技术，我们必须确保回归技术对于研究问题的适用性，才能相信回归结果是可靠的。识别回归技术的适用性，我们需要对回归分析进行诊断，诊断内容是线性回归最基本的六个假设是否成立，即

• 误差项是一个期望为0的随机变量；
• 对于解释变量的所有观测值，随机误差项有相同的方差；
• 随机误差项彼此不相关；
• 解释变量是确定性变量，不是随机变量，与随机误差项彼此之间相互独立；
• 解释变量之间不存在精确的（完全的）线性关系，即解释变量的样本观测值矩阵是满秩矩阵；
• 随机误差项服从正态分布。

那么，当我们遇到被解释变量为分类变量这一特殊的情境时，如果能够使用普通线性回归技术，就必须要满足以上所提到的六个基本假设，我们来进行一个简单的模拟。

我使用一个火箭发射成功与否的数据集来进行接下来的测试，首先我们读取数据集。

import numpy as np
import pandas as pd
data = pd.read_csv("challenger.csv")
data.drop(columns=['Unnamed: 0'], inplace=True)

数据集如下：

	num_at_risk		distress	launch_temp		leak_check_pressure		order
0	6				1			70				50						2
1	6				0			69				50						3
2	6				0			68				50						4
3	6				0			67				50						5
4	6				0			72				50						6
5	6				0			73				100						7
6	6				0			70				100						8
7	6				1			57				200						9
8	6				1			63				200						10
9	6				1			70				200						11
10	6				0			78				200						12
11	6				0			67				200						13
13	6				0			67				200						15
14	6				0			75				200						16
15	6				0			70				200						17
16	6				0			81				200						18		
17	6				0			76				200						19
18	6				0			79				200						20
19	6				0			75				200						21
20	6				0			76				200						22
21	6				1			58				200						23

我们使用statsmodels提供的线性回归分析API来完成回归，然后进行简单的可视化

import statsmodels.formula.api as smf
model = smf.ols('distress ~ num_at_risk + launch_temp + leak_check_pressure + order', data = data)
result = model.fit()
# result.summary()
import matplotlib.pyplot as plt
plt.figure(figsize = (10, 8), dpi = 80)
plt.scatter(result.fittedvalues, result.resid)
plt.plot([-0.3, 1.3], [0, 0], color = "black")
plt.show()

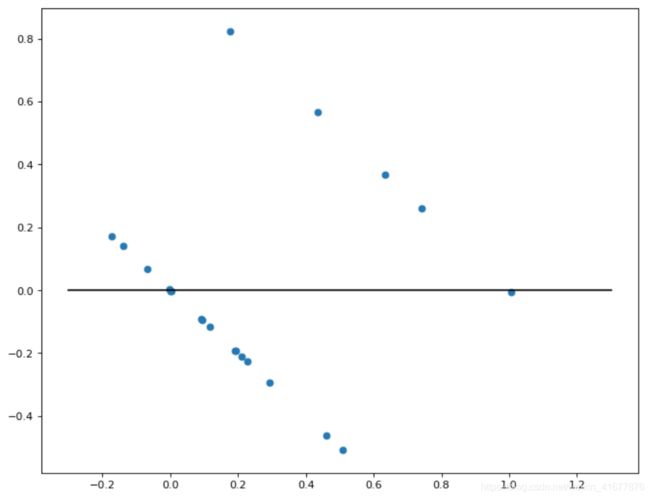
通过观察图像，我们不难看出，在使用普通线性回归技术来完成离散型变量回归时，上文提到的第一个和第二个假设都被打破了，即

• 误差项期望值不为0；
• 随机误差项方差随解释变量观测值的变化而变化。

因此，使用普通线性回归似乎在分类变量回归的情景下就不再是一个很合适的方法了，因此我们使用Link函数构建了适用于分类变量的回归技术。

什么是Link函数？

考虑一个最简单的二分类问题，我们如果使用普通线性回归技术来进行一个二分类问题的回归，结果就会像上面那张图一样，得到的预测值不是类别标签，而是一条线上任意的一个点，这显然不是我们想要的结果。
为了解决这个问题，我们引入了Link function的概念。什么是Link finction呢？其实它就是一个对于普通线性回归结果的非线性变化，目的是将现象回归的结果缩放成0到1之间的一个值。如果有了这个变化，回归后的拟合值就有了意义，因为这个数可以被视作分至指定类别的概率，可以支撑我们做类别预测的判断了。
最流行的Link函数有两种，一个是Probit，一个是Logit（即我们常说的Logistic回归），它们的函数表达式分别是：

• $Probit\left(z\right)=\Phi \left(z\right)={\int }_{-\infty }^z\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(-\frac{z^2}{2}\right)$
• $Logit\left(z\right)=\frac{\exp (z)}{1+\exp \left(z\right)}$

对应的图像为：

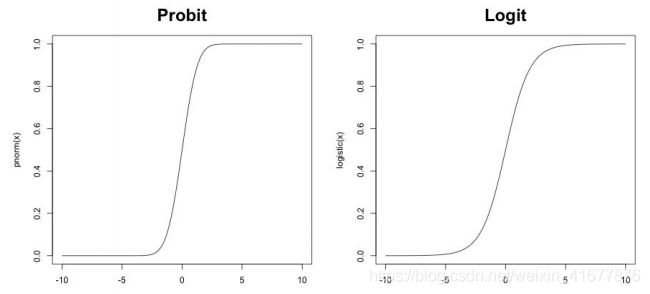
其实两者差距不大，Probit相对而言更加陡峭，Logit的转化则更柔和一些。

如何实现（statsmodels&sklearn）？

接下来我介绍两种在Python中进行分类变量回归的技术，先引入必要的工具和数据

import pandas as pd
import numpy as np
from sklearn import svm
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import label_binarize
from sklearn.metrics import confusion_matrix, classification_report
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
import statsmodels.api as sm
from statsmodels.discrete.discrete_model import Logit, Probit, MNLogit
from pylab import mpl
import plotly.graph_objects as go
import warnings
import matplotlib as mpl
warnings.filterwarnings('ignore')
#设置风格、尺度
sns.set_style('whitegrid')
sns.set_context('paper')
wine = pd.read_csv('winequality-red.csv')

数据可在下方链接下载：
红酒质量数据集下载

statsmodels（统计学分析场景推荐）

先把问题简化为一个二分类问题

X = wine.iloc[:, :-1]
Y = wine['quality']
binary_Y = []
for i in range(len(Y)):
    if Y[i] <=5:
        binary_Y.append(0)
    else:
        binary_Y.append(1)

Probit

probit_model = Probit(binary_Y, sm.add_constant(X))
result = probit_model.fit()
result.summary()

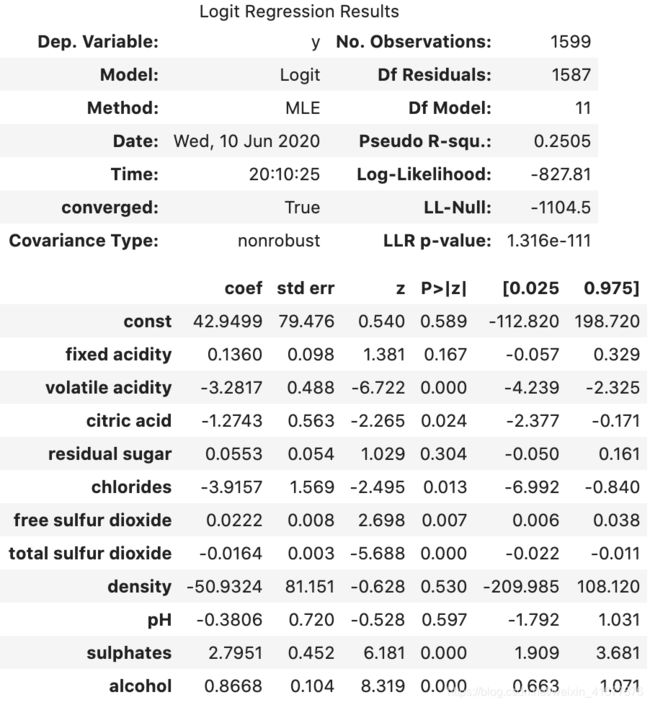
Logit

logist_model = Logit(binary_Y, sm.add_constant(X))
result = logist_model.fit()
result.summary()

MNLogit（Multinormal）

MNLogit就是当分类变量非二分类，而是多分类时的Logistic回归方法，具体实现很简单。（输出表很长，就不展示了）

mnLogit_model = MNLogit(Y, sm.add_constant(X))
result = mnLogit_model.fit()
result.summary()

sklearn（机器学习场景推荐）

sklearn也封装有Logistic回归的方法，也可以实现statsmodels类似的功能，但是可视化表格却非常的差劲，因此在统计学分析（Inference）里面我们一般不太使用sklearn。但是如果把回归技术用于预测目的的话，我们也是可以选择sklearn的。以下展示使用sklearn进行多变量Logistic回归的模型训练效果。

logit_model = LogisticRegression(multi_class='multinomial', penalty = 'l2')
logit_model.fit(X, Y)
predict = logit_model.predict(X)
y_one_hot = label_binarize(Y, np.arange(3, 9))
predict_proba = logit_model.predict_proba(X)
fpr, tpr, threshold = roc_curve(y_one_hot.ravel(), predict_proba.ravel()) ###计算真正率和假正率
roc_auc = auc(fpr,tpr) ###计算auc的值
mpl.rcParams['font.family'] = 'sans-serif'
mpl.rcParams['font.sans-serif'] = 'NSimSun,Times New Roman'
font = {
     'family': 'sans-serif',
            'color': 'k',
            'weight': 'bold',
            'size': 20,}
plt.figure()
plt.figure(figsize=(12,10), dpi=80)
plt.plot(fpr, tpr, color='darkorange',
             lw=5, label='ROC curve (area = %0.3f)' % roc_auc) ###假正率为横坐标，真正率为纵坐标做曲线
plt.plot([0, 1], [0, 1], color='navy', lw=3, linestyle='--')
plt.xlim([-0.01, 1.01])
plt.ylim([-0.01, 1.01])
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.xlabel('False Positive Rate', fontsize=15)
plt.ylabel('True Positive Rate', fontsize=15)
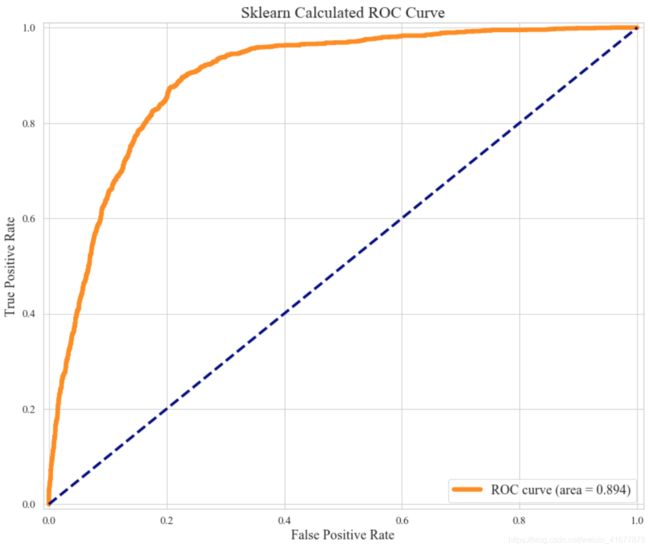
plt.title('Sklearn Calculated ROC Curve', fontsize=18)
plt.legend(loc="lower right", fontsize=15)
plt.show()