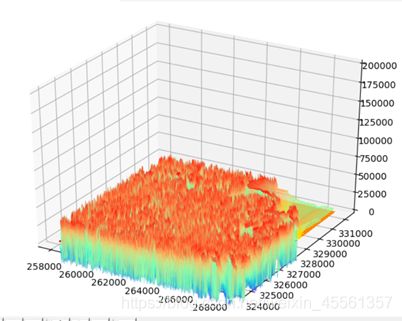
基于python实现利用DEM数据计算坡度、坡向

基本概念

DEM数据

DataMark:CNSDTF-DEM
Version:1.0
Unit:M
Alpha:0.000000
Compress:0.000000
X0:258000.000
Y0:324000.000
DX:22.500
DY:22.500
Row:321
Col:481
ValueType:Integer
Hzoom:1000
 192743  191068  187814  181388  173357  165286  157185  152266  147335  142391 
 139052  137327  135608  130633  124014  117372  118908  123706  128495  133265 
 138026  139540  139440  139337  135994  131025  127669  124312  120947  119208 
 125633  135280  141643  149598  155913  160612  162106  163600  160300  160203 
 158500  156795  155094  151780  148466  143534  138590  133632  130287  126935 
 125208  126733  133122  136259  137773  139280  142407  143916  142199  142101 

坡度

坡度是法线与铅垂线之间的夹角。如图2.2所示，利用坡度计算公式$\alpha =arctan\sqrt{f_x^2+f_y^2}$ ，进行求解。
坡向

坡向是法线在水平面上的投影与正北方向之间的夹角（顺时针度量）。如图2.3所示，利用坡向计算公式$A=\arctan \frac{f_y}{f_x}$ ， 求解。

程序流程

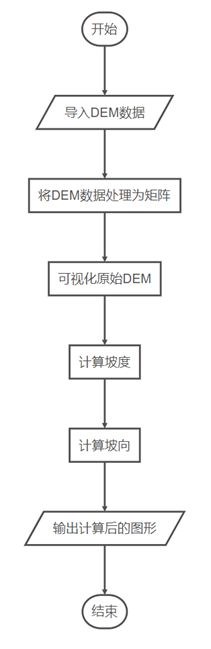
2）计算各点梯度

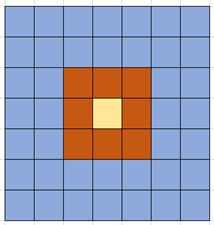
如图3.5所示，可以利用像下面的公式写一个函数进行计算，$slop{e}_x=\frac{e_1-e_3}{2\times dsizex}slop{e}_y=\frac{e_4-e_2}{2\times dsizey}$
。首先计算3*3DEM格网数据的X,Y方向的变化。对于整幅图而言，由于本图像元点不是特别多，故对于边缘的点处理时，可以在栅格点外再加一圈栅格便于求梯度。而添加点的方式只需要把原本边缘的栅格点的高程值复制一遍即可，如图3.6所示。

3)解算坡度、坡向
如图3.5所示，可以利用下面的公式计算求得坡度和坡向$slop=\arctan \sqrt{slop{e}_x^2+slop{e}_y^2}A=\arctan \frac{slop{e}_y}{slop{e}_x}$。在这一过程中可以整体进行计算，从而较为方便地获得坡度和坡向的二维矩阵。
4)可视化
利用python中的绘图库matplotlib，编写了一个可视化函数，利用plot里面的imshow，将之前计算得到的二维矩阵存进去，最后以栅格的方式显示。对于三维DEM显示，利用Axes3D的方法，利用DEM文件中的起始坐标和分辨率推算出各个栅格的坐标，对应出高程值，绘制出三维图形。

程序代码

DEMclass模块

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cbook
from matplotlib import cm
from matplotlib.colors import LightSource
import matplotlib.pyplot as plt
import numpy as np
import re
import math
#####读取文件并处理成numpy并返回
def readfile():
    with open('datas.DEM', 'r', encoding='utf-8')as file:
        datas = file.readlines()[13:]
    list1 = []
    strs = ""
    row = 321
    col = 481
    npdata = np.zeros((row, col), dtype=np.int16)
    for data in datas:
        data = data.strip()
        if len(data) > 20:
            strs = strs + "   " + data
        if len(data) < 20:
            strs = strs + "   " + data
            list1.append(strs)
            strs = ""

    for i, sitem in enumerate(list1):
        item = str(sitem).strip()
        # item=item.split("  ")
        item = re.findall(r'\d+', item)
        for j, one in enumerate(item):  # i是序号，one是数值
            npdata[i][j] = int(one)
    return npdata
#####在原栅格图像周围加一圈并返回
def AddRound(npgrid):
    ny, nx = npgrid.shape  # ny:行数，nx:列数
    zbc=np.zeros((ny+2,nx+2))
    zbc[1:-1,1:-1]=npgrid
    #四边
    zbc[0,1:-1]=npgrid[0,:]
    zbc[-1,1:-1]=npgrid[-1,:]
    zbc[1:-1,0]=npgrid[:,0]
    zbc[1:-1,-1]=npgrid[:,-1]
    #角点
    zbc[0,0]=npgrid[0,0]
    zbc[0,-1]=npgrid[0,-1]
    zbc[-1,0]=npgrid[-1,0]
    zbc[-1,-1]=npgrid[-1,0]
    return zbc
#####计算xy方向的梯度
def Cacdxdy(npgrid,sizex,sizey):
    zbc=AddRound(npgrid)
    dx=((zbc[1:-1,:-2])-(zbc[1:-1,2:]))/sizex/2/1000
    dy=((zbc[2:,1:-1])-(zbc[:-2,1:-1]))/sizey/2/1000
    dx=dx[1:-1,1:-1]
    dy=dy[1:-1,1:-1]
    np.savetxt("dxdy.csv",dx,delimiter=",")
    return dx,dy
####计算坡度\坡向
def CacSlopAsp(dx,dy):
    slope=(np.arctan(np.sqrt(dx*dx+dy*dy)))*57.29578  #转换成°
    slope=slope[1:-1,1:-1]
    #坡向
    a=np.zeros([dx.shape[0],dx.shape[1]]).astype(np.float32)
    for i in range(dx.shape[0]):
        for j in range(dx.shape[1]):
            x=float(dx[i,j])
            y=float(dy[i,j])
            if (x==0.)& (y==0.):
                a[i,j]=-1
            elif x==0.:
                if y>0.:
                    a[i,j]=0.
                else:
                    a[i,j]=180.
            elif y==0.:
                if x>0:
                    a[i,j]=90.
                else:
                    a[i,j]=270.
            else:
                a[i,j]=float(math.atan(y/x))*57.29578
                if a[i,j]<0.:
                    a[i,j]=90.-a[i,j]
                elif a[i,j]>90.:
                    a[i,j]=450.-a[i,j]
                else:
                    a[i,j]=90.-a[i,j]
    return slope,a
####绘制平面栅格图
def Drawgrid(judge,pre=[],A=[],strs=""):
    if judge==0:
        if strs == "":
            plt.imshow(A, interpolation='nearest', cmap=plt.cm.hot, origin='lower')  # cmap='bone'  cmap=plt.cm.hot
            plt.colorbar(shrink=0.8)
            plt.xticks(())
            plt.yticks(())
            plt.show()
        else:
            plt.imshow(A, interpolation='nearest', cmap=strs, origin='lower')  # cmap='bone'  cmap=plt.cm.hot
            plt.colorbar(shrink=0.8)
            xt=range(258000, 268822,22)
            yt=range(324000, 331222,22)
            plt.xticks(())
            plt.yticks(())
            plt.show()
    elif judge==1:
        fig = plt.figure()
        ax = Axes3D(fig)
        # X = np.arange(1,482,1)
        # Y = np.arange(1,322,1)
        X = np.arange(258000.000, 268822.500, 22.5)
        Y = np.arange(324000.000, 331222.500, 22.5)
        X, Y = np.meshgrid(X, Y)
        Z = pre
        ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.get_cmap('rainbow'))  # cmap=plt.get_cmap('rainbow')
        ax.contourf(X, Y, Z, zdir='z', offset=-2, cmap=plt.cm.hot)
        ax.set_zlim(0, 200000)
        plt.show()

主函数

import DEMclass as dem
from DEMclass import Drawgrid
import numpy as np
####程序入口
if __name__=='__main__':
    npgrid=dem.readfile()
    pre=npgrid
    npgrid=dem.AddRound(npgrid)
    dx,dy=dem.Cacdxdy(npgrid,22.5,22.5)
    slope,arf=dem.CacSlopAsp(dx,dy)
    dem.np.savetxt("slope.csv",slope,delimiter=",")
    #绘制三维DEM
    Drawgrid(judge=1,pre=pre)
    #绘制二维DEM
    Drawgrid(judge=0,A=pre,strs="bone")
    #绘制坡度图
    Drawgrid(judge=0,A=slope,strs="rainbow")
    #绘制坡向图
    Drawgrid(judge=0,A=arf)

效果图

三维图：

二维DEM：

坡度图：

坡向图：

参考资料

1.Python的地形三维可视化——简介Matplotlib和gdal
https://blog.csdn.net/allenlu2008/article/details/51880333
2.Pycharm中配置GDAL库的一种方法
https://blog.csdn.net/qq_35960361/article/details/96438650
3.python 调用gdal 处理dem数据
https://blog.csdn.net/qq_15642411/article/details/79123677
4.适用于Python扩展程序包的非官方Windows二进制文件——GDAL
https://www.lfd.uci.edu/~gohlke/pythonlibs/#gdal
5.python gdal安装与简单使用
https://blog.csdn.net/nima1994/article/details/79207805/
pip install GDAL-2.4.1-cp37-cp37m-win_amd64.whl
6.（目测有用）【GDAL】python读取DEM计算坡度与坡向
https://blog.csdn.net/qq_37935516/article/details/85028979
7.arcgis计算坡度、坡向
http://help.arcgis.com/zh-cn/arcgisdesktop/10.0/help/index.html#//009z000000vz000000
8.C语言实现GDAL使用DEM数据计算坡度坡向
https://blog.csdn.net/liminlu0314/article/details/8498985
9.gdal在python功能（官方）
https://gdal.org/python/index.html
10.玩转python的正则表达式|提取字符串中的所有数字
https://blog.csdn.net/guanyonglai/article/details/89512659
https://blog.csdn.net/u011436427/article/details/82628597
可视化
1.三维图（目测有用）
https://blog.51cto.com/9291927/2435621
2.地图+热力图（可以用于坡度坡向）
https://www.zhihu.com/question/33783546
3.统计
https://www.cnblogs.com/dudududu/p/9149762.html
4.turtle库
https://blog.csdn.net/weixin_44078196/article/details/10065651