Python-Numpy多维数组 -- 矩阵库、线性代数、绘图库Matplotlib
一、Numpy - 矩阵库
NumPy 包包含一个 Matrix库numpy.matlib。此模块的函数返回矩阵而不是返回ndarray对象。
1.matlib.empty()函数返回一个新的矩阵,而不初始化元素。 该函数接受以下参数。
numpy.matlib.empty(shape, dtype, order)
| 序号 | 参数及描述 |
|---|---|
| 1. | shape 定义新矩阵形状的整数或整数元组 |
| 2. | Dtype 可选,输出的数据类型 |
| 3. | order C 或者 F |
demo
import numpy.matlib
import numpy as np
print np.matlib.empty((2,2))
# 填充为随机数据
输出如下:
[[ 2.12199579e-314, 4.24399158e-314]
[ 4.24399158e-314, 2.12199579e-314]]2.numpy.matlib.zeros()函数返回以零填充的矩阵。
import numpy.matlib
import numpy as np
print np.matlib.zeros((2,2))
输出如下:
[[ 0. 0.]
[ 0. 0.]])3.numpy.matlib.ones()函数返回以一填充的矩阵。
import numpy.matlib
import numpy as np
print np.matlib.ones((2,2))
输出如下:
[[ 1. 1.]
[ 1. 1.]]
4.numpy.matlib.eye()函数返回一个矩阵,对角线元素为 1,其他位置为零。 该函数接受以下参数。numpy.matlib.eye(n, M,k, dtype)
| 序号 | 参数及描述 |
|---|---|
| 1. | n 返回矩阵的行数 |
| 2. | M 返回矩阵的列数,默认为n |
| 3. | k 对角线的索引 |
| 4. | dtype 输出的数据类型 |
demo
import numpy.matlib
import numpy as np
print np.matlib.eye(n = 3, M = 4, k = 0, dtype = float)
输出如下:
[[ 1. 0. 0. 0.]
[ 0. 1. 0. 0.]
[ 0. 0. 1. 0.]])5.numpy.matlib.identity()函数返回给定大小的单位矩阵。单位矩阵是主对角线元素都为 1 的方阵。
import numpy.matlib
import numpy as np
print np.matlib.identity(5, dtype = float)
输出如下:
[[ 1. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. 0. 1. 0.]
[ 0. 0. 0. 0. 1.]]
6.numpy.matlib.rand()函数返回给定大小的填充随机值的矩阵。
demo
import numpy.matlib
import numpy as np
print np.matlib.rand(3,3)
输出如下:
[[ 0.82674464 0.57206837 0.15497519]
[ 0.33857374 0.35742401 0.90895076]
[ 0.03968467 0.13962089 0.39665201]]
注意,矩阵总是二维的,而ndarray是一个 n 维数组。 两个对象都是可互换的。
demo1
import numpy.matlib
import numpy as np
i = np.matrix('1,2;3,4')
print i
输出如下:
[[1 2]
[3 4]]
demo2
import numpy.matlib
import numpy as np
j = np.asarray(i)
print j
输出如下:
[[1 2]
[3 4]]
demo3
import numpy.matlib
import numpy as np
k = np.asmatrix (j)
print k
输出如下:
[[1 2]
[3 4]]二、Numpy - 线性代数
Numpy 包包含numpy.linalg模块,提供线性代数所需的所有功能。 此模块中的一些重要功能如下表所述。
| 序号 | 函数及描述 |
|---|---|
| 1. | dot 两个数组的点积 |
| 2. | vdot 两个向量的点积 |
| 3. | inner 两个数组的内积 |
| 4. | matmul 两个数组的矩阵积 |
| 5. | determinant 数组的行列式 |
| 6. | solve 求解线性矩阵方程 |
| 7. | inv 寻找矩阵的乘法逆矩阵 |
1.numpy.dot()返回两个数组的点积。 对于二维向量,其等效于矩阵乘法。 对于一维数组,它是向量的内积。 对于 N 维数组,它是a的最后一个轴上的和与b的倒数第二个轴的乘积。
import numpy.matlib
import numpy as np
a = np.array([[1,2],[3,4]])
b = np.array([[11,12],[13,14]])
np.dot(a,b)
输出如下:
[[37 40]
[85 92]]要注意点积计算为:
[[1*11+2*13, 1*12+2*14],[3*11+4*13, 3*12+4*14]]
2.numpy.vdot()函数返回两个向量的点积。 如果第一个参数是复数,那么它的共轭复数会用于计算。 如果参数id是多维数组,它会被展开。
demo
import numpy as np
a = np.array([[1,2],[3,4]])
b = np.array([[11,12],[13,14]])
print np.vdot(a,b)
输出如下:130
注意:1*11 + 2*12 + 3*13 + 4*14 = 130。3.numpy.inner()函数返回一维数组的向量内积。 对于更高的维度,它返回最后一个轴上的和的乘积。
demo
import numpy as np
print np.inner(np.array([1,2,3]),np.array([0,1,0]))
# 等价于 1*0+2*1+3*0
输出如下:
# 多维数组示例
import numpy as np
a = np.array([[1,2], [3,4]])
print '数组 a:'
print a
b = np.array([[11, 12], [13, 14]])
print '数组 b:'
print b
print '内积:'
print np.inner(a,b)
输出如下:
数组 a:
[[1 2]
[3 4]]
数组 b:
[[11 12]
[13 14]]
内积:
[[35 41]
[81 95]]
上面的例子中,内积计算如下:
1*11+2*12, 1*13+2*14
3*11+4*12, 3*13+4*144.numpy.matmul函数返回两个数组的矩阵乘积。 虽然它返回二维数组的正常乘积,但如果任一参数的维数大于2,则将其视为存在于最后两个索引的矩阵的栈,并进行相应广播。
另一方面,如果任一参数是一维数组,则通过在其维度上附加 1 来将其提升为矩阵,并在乘法之后被去除。
# 对于二维数组,它就是矩阵乘法
import numpy.matlib
import numpy as np
a = [[1,0],[0,1]]
b = [[4,1],[2,2]]
print np.matmul(a,b)
输出如下:
[[4 1]
[2 2]]
# 二维和一维运算
import numpy.matlib
import numpy as np
a = [[1,0],[0,1]]
b = [1,2]
print np.matmul(a,b)
print np.matmul(b,a)
输出如下:
[1 2]
[1 2]
# 维度大于二的数组
import numpy.matlib
import numpy as np
a = np.arange(8).reshape(2,2,2)
b = np.arange(4).reshape(2,2)
print np.matmul(a,b)
输出如下:
[[[2 3]
[6 11]]
[[10 19]
[14 27]]]5.numpy.linalg.det()行列式在线性代数中是非常有用的值。 它从方阵的对角元素计算。 对于 2×2 矩阵,它是左上和右下元素的乘积与其他两个的乘积的差。
换句话说,对于矩阵[[a,b],[c,d]],行列式计算为ad-bc。 较大的方阵被认为是 2×2 矩阵的组合。
numpy.linalg.det()函数计算输入矩阵的行列式。
import numpy as np
a = np.array([[1,2], [3,4]])
print np.linalg.det(a)
输出如下:-2.0
b = np.array([[6,1,1], [4, -2, 5], [2,8,7]])
print b
print np.linalg.det(b)
print 6*(-2*7 - 5*8) - 1*(4*7 - 5*2) + 1*(4*8 - -2*2)
输出如下:
[[ 6 1 1]
[ 4 -2 5]
[ 2 8 7]]
-306.0
-306
6.numpy.linalg.solve()
numpy.linalg.solve()函数给出了矩阵形式的线性方程的解。
考虑以下线性方程:
-
x + y + z = 6 -
2y + 5z = -4 -
2x + 5y - z = 27
可以使用矩阵表示为:
如果矩阵成为A、X和B,方程变为:
AX = B
或
X = A^(-1)B
7.numpy.linalg.inv()来计算矩阵的逆。 矩阵的逆是这样的,如果它乘以原始矩阵,则得到单位矩阵。
demo
import numpy as np
x = np.array([[1,2],[3,4]])
y = np.linalg.inv(x)
print x
print y
print np.dot(x,y)
输出如下:
[[1 2]
[3 4]]
[[-2. 1. ]
[ 1.5 -0.5]]
[[ 1.00000000e+00 1.11022302e-16]
[ 0.00000000e+00 1.00000000e+00]]
# 现在让我们在示例中创建一个矩阵A的逆。
import numpy as np
a = np.array([[1,1,1],[0,2,5],[2,5,-1]])
print '数组 a:'
print a
ainv = np.linalg.inv(a)
print 'a 的逆:'
print ainv
print '矩阵 b:'
b = np.array([[6],[-4],[27]])
print b
print '计算:A^(-1)B:'
x = np.linalg.solve(a,b)
print x
# 这就是线性方向 x = 5, y = 3, z = -2 的解
输出如下:
数组 a:
[[ 1 1 1]
[ 0 2 5]
[ 2 5 -1]]
a 的逆:
[[ 1.28571429 -0.28571429 -0.14285714]
[-0.47619048 0.14285714 0.23809524]
[ 0.19047619 0.14285714 -0.0952381 ]]
矩阵 b:
[[ 6]
[-4]
[27]]
计算:A^(-1)B:
[[ 5.]
[ 3.]
[-2.]]
结果也可以使用下列函数获取x = np.dot(ainv,b)三、Numpy - Matplotlib
Matplotlib 是 Python 的绘图库。 它可与 NumPy 一起使用,提供了一种有效的 MatLab 开源替代方案。 它也可以和图形工具包一起使用,如 PyQt 和 wxPython。
通常,通过添加以下语句将包导入到 Python 脚本中:
-
from matplotlib import pyplot as plt
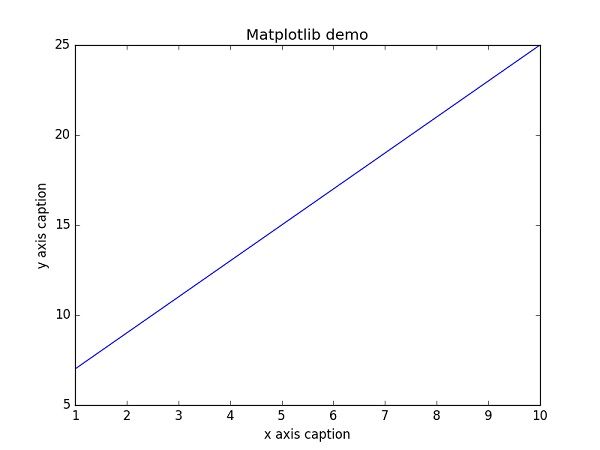
这里pyplot()是 matplotlib 库中最重要的函数,用于绘制 2D 数据。 以下脚本绘制方程y = 2x + 5:
示例
import numpy as np
from matplotlib import pyplot as plt
x = np.arange(1,11)
y = 2 * x + 5
plt.title("Matplotlib demo")
plt.xlabel("x axis caption")
plt.ylabel("y axis caption")
plt.plot(x,y) plt.show()ndarray对象x由np.arange()函数创建为x轴上的值。y轴上的对应值存储在另一个数组对象y中。 这些值使用matplotlib软件包的pyplot子模块的plot()函数绘制。
图形由show()函数展示。
上面的代码应该产生以下输出:
Matplotlib Demo
作为线性图的替代,可以通过向plot()函数添加格式字符串来显示离散值。 可以使用以下格式化字符。
| 字符 | 描述 | |
|---|---|---|
'-' |
实线样式 | |
'--' |
短横线样式 | |
'-.' |
点划线样式 | |
':' |
虚线样式 | |
'.' |
点标记 | |
',' |
像素标记 | |
'o' |
圆标记 | |
'v' |
倒三角标记 | |
'^' |
正三角标记 | |
'<' |
左三角标记 | |
'>' |
右三角标记 | |
'1' |
下箭头标记 | |
'2' |
上箭头标记 | |
'3' |
左箭头标记 | |
'4' |
右箭头标记 | |
's' |
正方形标记 | |
'p' |
五边形标记 | |
'*' |
星形标记 | |
'h' |
六边形标记 1 | |
'H' |
六边形标记 2 | |
'+' |
加号标记 | |
'x' |
X 标记 | |
'D' |
菱形标记 | |
'd' |
窄菱形标记 | |
| `' | '` | 竖直线标记 |
'_' |
水平线标记 |
还定义了以下颜色缩写。
| 字符 | 颜色 |
|---|---|
'b' |
蓝色 |
'g' |
绿色 |
'r' |
红色 |
'c' |
青色 |
'm' |
品红色 |
'y' |
黄色 |
'k' |
黑色 |
'w' |
白色 |
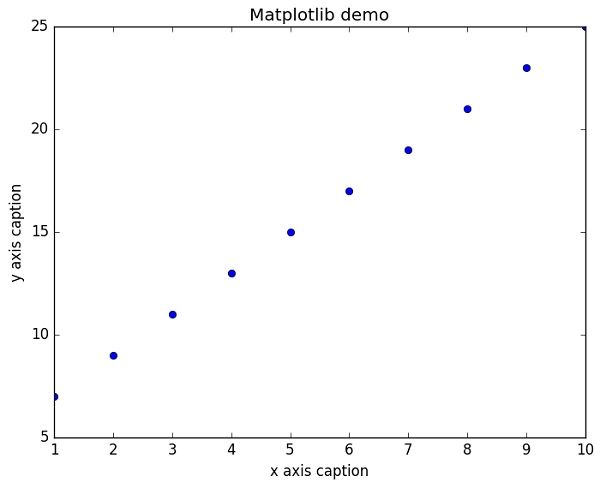
要显示圆来代表点,而不是上面示例中的线,请使用ob作为plot()函数中的格式字符串。
示例
import numpy as np
from matplotlib import pyplot as plt
x = np.arange(1,11)
y = 2 * x + 5
plt.title("Matplotlib demo")
plt.xlabel("x axis caption")
plt.ylabel("y axis caption")
plt.plot(x,y,"ob")
plt.show()上面的代码应该产生以下输出:
Color Abbreviation
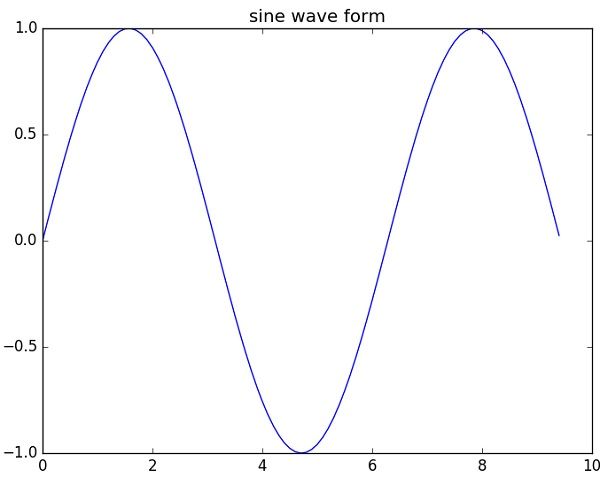
绘制正弦波
以下脚本使用 matplotlib 生成正弦波图。
示例
import numpy as np
import matplotlib.pyplot as plt
# 计算正弦曲线上点的 x 和 y 坐标
x = np.arange(0, 3 * np.pi, 0.1)
y = np.sin(x)
plt.title("sine wave form")
# 使用 matplotlib 来绘制点
plt.plot(x, y)
plt.show()Sine Wave
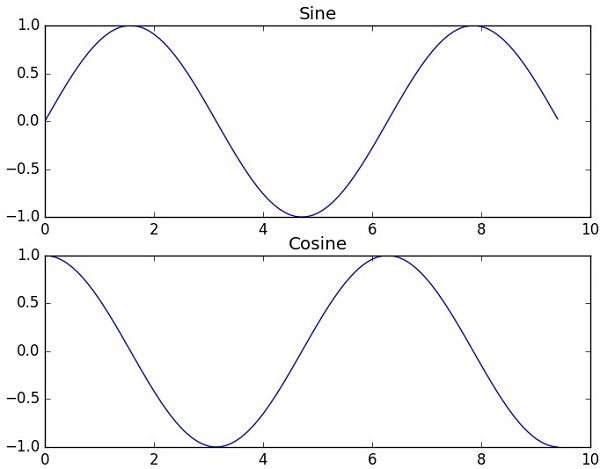
subplot()
subplot()函数允许你在同一图中绘制不同的东西。 在下面的脚本中,绘制正弦和余弦值。
示例
import numpy as np
import matplotlib.pyplot as plt
# 计算正弦和余弦曲线上的点的 x 和 y 坐标
x = np.arange(0, 3 * np.pi, 0.1)
y_sin = np.sin(x)
y_cos = np.cos(x)
# 建立 subplot 网格,高为 2,宽为 1
# 激活第一个 subplot
plt.subplot(2, 1, 1)
# 绘制第一个图像
plt.plot(x, y_sin)
plt.title('Sine')
# 将第二个 subplot 激活,并绘制第二个图像
plt.subplot(2, 1, 2)
plt.plot(x, y_cos)
plt.title('Cosine')
# 展示图像
plt.show()上面的代码应该产生以下输出:
Sub Plot
bar()
pyplot子模块提供bar()函数来生成条形图。 以下示例生成两组x和y数组的条形图。
示例
from matplotlib import pyplot as plt
x = [5,8,10]
y = [12,16,6]
x2 = [6,9,11]
y2 = [6,15,7]
plt.bar(x, y, align = 'center')
plt.bar(x2, y2, color = 'g', align = 'center')
plt.title('Bar graph')
plt.ylabel('Y axis')
plt.xlabel('X axis')
plt.show()四、Numpy - 使用 Matplotlib 绘制直方图
NumPy 有一个numpy.histogram()函数,它是数据的频率分布的图形表示。 水平尺寸相等的矩形对应于类间隔,称为bin,变量height对应于频率。
1.numpy.histogram()函数将输入数组和bin作为两个参数。 bin数组中的连续元素用作每个bin的边界。
import numpy as np
a = np.array([22,87,5,43,56,73,55,54,11,20,51,5,79,31,27]) ]
np.histogram(a,bins = [0,20,40,60,80,100])
hist,bins = np.histogram(a,bins = [0,20,40,60,80,100])
print hist
print bins
输出如下:
[3 4 5 2 1]
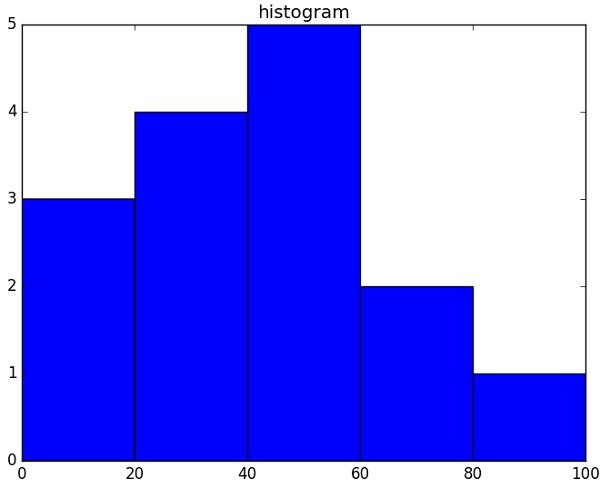
[0 20 40 60 80 100]2.plt()Matplotlib 可以将直方图的数字表示转换为图形。 pyplot子模块的plt()函数将包含数据和bin数组的数组作为参数,并转换为直方图。
from matplotlib import pyplot as plt
import numpy as np
a = np.array([22,87,5,43,56,73,55,54,11,20,51,5,79,31,27])
plt.hist(a, bins = [0,20,40,60,80,100])
plt.title("histogram")
plt.show()输出如下:
Histogram Plot
四、Numpy - IO
ndarray对象可以保存到磁盘文件并从磁盘文件加载。 可用的 IO 功能有:
-
load()和save()函数处理 numPy 二进制文件(带npy扩展名) -
loadtxt()和savetxt()函数处理正常的文本文件
NumPy 为ndarray对象引入了一个简单的文件格式。 这个npy文件在磁盘文件中,存储重建ndarray所需的数据、图形、dtype和其他信息,以便正确获取数组,即使该文件在具有不同架构的另一台机器上。
1.numpy.save()文件将输入数组存储在具有npy扩展名的磁盘文件中。
import numpy as np
a = np.array([1,2,3,4,5])
np.save('outfile',a)
为了从outfile.npy重建数组,请使用load()函数。
import numpy as np
b = np.load('outfile.npy')
print b
输出如下:
array([1, 2, 3, 4, 5])save()和load()函数接受一个附加的布尔参数allow_pickles。 Python 中的pickle用于在保存到磁盘文件或从磁盘文件读取之前,对对象进行序列化和反序列化。
2.savetxt()以简单文本文件格式存储和获取数组数据,是通过savetxt()和loadtx()函数完成的。
示例
import numpy as np
a = np.array([1,2,3,4,5])
np.savetxt('out.txt',a)
b = np.loadtxt('out.txt')
print b
输出如下:
[ 1. 2. 3. 4. 5.]
savetxt()和loadtxt()数接受附加的可选参数,例如页首,页尾和分隔符。