NLP实践四：LDA主题模型

LDA主题模型

基本原理

LSA（Latent semantic analysis，隐性语义分析）、pLSA（Probabilistic latent semantic analysis，概率隐性语义分析）和 LDA（Latent Dirichlet allocation，隐狄利克雷分配）这三种模型都可以归类到话题模型（Topic model，或称为主题模型）中。相对于比较简单的向量空间模型，主题模型通过引入主题这个概念，更进一步地对文本进行语义层面上的理解。

LSA

LSA 模型就是对词-文档共现矩阵进行SVD，从而得到词和文档映射到抽象出的topic上的向量表示，之前的一篇博客稍微提到过一点。LSA 通过将词映射到topic上得到distributional representation（词的分布表示），进而缓解文档检索、文档相似度计算等任务中所面临的同义词（多词一义）问题：比如我搜索“Java 讲义”，如果系统只是用字符匹配来检索的话，是不会返回一篇出现了“Java 课件”但通篇没出现“讲义”这个词的文档的。所以说，单纯地从词-文档共现矩阵取出词向量表示和文档向量表示的向量空间模型，尽管利用了大规模文档集的统计信息，仍然是无法直接从“语义”这个层面上去理解文本的。但是 LSA 这种将词映射到topic上的向量表示，很难去应对一词多义问题：比如“Java”这个词既可能指编程语言，也可能指爪哇岛，即使这两种含义的“Java”都在文档集里出现过，得到的 LSA 模型也无法很好地区分。

pLSA

pLSA 模型是有向图模型，将主题作为隐变量，构建了一个简单的贝叶斯网，采用EM算法估计模型参数。相比于 LSA 略显“随意”的SVD，pLSA 的统计基础更为牢固。

相比于 LDA 模型里涉及先验分布，pLSA 模型相对简单：观测变量为文档 $d_m\in \mathbb{D}$（文档集共 M 篇文档）、词 $w_n\in \mathbb{W}$（设词汇表共有 V 个互不相同的词），隐变量为主题 $z_k\in \mathbb{Z}$（共 K 个主题）。在给定文档集后，我们可以得到一个词-文档共现矩阵，每个元素 $n(d_m,w_n)$ 表示的是词 $w_n$ 在文档 $d_m$ 中的词频。也就是说，pLSA 模型也是基于词-文档共现矩阵的，不考虑词序
pLSA 模型通过以下过程来生成文档（记号里全部省去了对参数的依赖）：
(1) 以概率 $P(d_m)$ 选择一篇文档 $d_m$
(2) 以概率 $P(z_k|d_m)$ 得到一个主题 $z_k$
(3) 以概率 $P(w_n|z_k)$ 生成一个词 $w_n$
概率图模型如下所示

图里面的浅色节点代表不可观测的隐变量，方框是指变量重复（plate notation），内部方框表示的是文档 $d_m$ 的长度是 N，外部方框表示的是文档集共 M 篇文档。pLSA 模型的参数 $\theta$ 显而易见就是：$K\times M$ 个 $P(z_k|d_m)$ 、$V\times K$ 个 $P(w_n|z_k)$ 。$P(z_k|d_m)$ 表征的是给定文档在各个主题下的分布情况，文档在全部主题上服从多项式分布（共 M 个）；$P(w_n|z_k)$ 则表征给定主题的词语分布情况，主题在全部词语上服从多项式分布（共 K 个）。
拿到贝叶斯网当然先要看看联合分布咯。这个贝叶斯网表达的是如下的联合分布：
$$P(d_m,z_k,w_n)=P(d_m)P(z_k|d_m)P(w_n|z_k)$$
$$P(d_m,w_n)=P(d_m)P(w_n|d_m)$$
假设有一篇文档为 $w=(w_1,w_2,...,w_N)$ ，生成它的概率就是$$P(w|d_m)=\prod _{n=1}^{N}P(w_n|d_m)$$
我们看一下 $P(w_n|d_m)$ 的表达式。如果不考虑随机变量之间的条件独立性的话，有
$$P(w_n|d_m)=\sum _{k}P(z_k|d_m)P(w_n|z_k,d_m)$$
但是观察图模型中的 d 、z 、w 可以知道，它们三个是有向图模型里非常典型的 head-to-tail 的情况：当 z 已知时，d 和 w 条件独立，也就是
$$P(w_n|z_k,d_m)=P(w_n|z_k)$$
进而有
$$P(w_n|d_m)=\sum _{k}P(z_k|d_m)P(w_n|z_k)$$
所以最终的联合分布表达式为
$$P(d_m,w_n)=P(d_m)\sum _{k}P(z_k|d_m)P(w_n|z_k)$$
这样的话，我们要做的事就是从文档集里估计出上面的参数。pLSA 是频率学派的方法，将模型参数看作具体值，而不是有先验的随机变量。所以，考虑最大化对数似然函数：
$$\begin{array}{rl}L(\theta )& =\ln \prod _{m=1}^M\prod _{n=1}^{N}P(d_m,w_n{)}^{n(d_m,w_n)}\\ & =\sum _m\sum _{n}n(d_m,w_n)\ln ;P(d_m,w_n)\\ & =\sum _m\sum _{n}n(d_m,w_n)(\ln P(d_m)+\ln P(w_n|d_m))\\ & =\sum _m\sum _{n}n(d_m,w_n)\ln P(w_n|d_m)+\sum _m\sum _{n}n(d_m,w_n)\ln P(d_m)\end{array}$$
第二项可以直接去掉，那么不妨直接记：
$$\begin{array}{rl}L(\theta )& =\sum _m\sum _{n}n(d_m,w_n)\ln P(w_n|d_m)\\ & =\sum _m\sum _{n}n(d_m,w_n)\ln [\sum _{k}P(z_k|d_m)P(w_n|z_k)]\end{array}$$
参数估计：EM算法迭代求解
由于参数全部在求和号里被外层的log套住，所以很难直接求偏导数估计参数。到了这里，就轮到EM算法闪亮登场了。之前的一篇简单介绍EM的博客里解决的是这样的问题：观测变量 y ，隐变量 z ，参数 $\theta$ ，目标函数 $L(\theta )=\ln P(y)=\ln {\sum }_{k}P(z_k)P(y|z_k)$ （省略$\theta$依赖），Q函数 $Q(\theta ;{\theta }_t)={\mathbb{E}}_{z|y;{\theta }_t}[\ln P(y,z)]={\sum }_{k}P(z_k|y;{\theta }_t)\ln P(y,z)$ ，进而有 ${\theta }_{t+1}=\arg {\max }_{\theta }Q(\theta ;{\theta }_t)$ 来迭代求取。

1. E步，求期望
   那么，仿照上面的写法，对于 pLSA 模型来说，Q函数的形式为
   $$\begin{array}{rl}Q(\theta ;{\theta }_t)& =\sum _m\sum _{n}n(d_m,w_n){\mathbb{E}}_{z_k|w_n,d_m;{\theta }_t}[\ln P(w_n,z_k|d_m)]\\ & =\sum _m\sum _{n}n(d_m,w_n)\sum _{k}P(z_k|w_n,d_m;{\theta }_t)\ln P(w_n,z_k|d_m)\end{array}$$
   (1) 联合概率 $P(w_n,z_k|d_m)$ 的求解：
   $$P(w_n,z_k|d_m)=P(z_k|d_m)P(w_n|z_k,d_m)=P(z_k|d_m)P(w_n|z_k)$$
   (2) $P(z_k|w_n,d_m;{\theta }_t)$ 的求解：
   所谓的 ${\theta }_t$ 实际上就是上一步迭代的全部 $K\times M$ 个 $P(z_k|d_m)$ 和 $V\times K$ 个 $P(w_n|z_k)$ 。为了避免歧义，将时间步 $t$ 迭代得到的参数值加一个下标 $t$ 。
   $$\begin{array}{rl}P(z_k|w_n,d_m;{\theta }_t)& amp;=\frac{P_t(z_k,w_n,d_m)}{P_t(w_n,d_m)}=\frac{P_t(d_m)P_t(z_k|d_m)P_t(w_n|z_k)}{P_t(d_m)P_t(w_n|d_m)}\\ & amp;=\frac{P_t(z_k|d_m)P_t(w_n|z_k)}{P_t(w_n|d_m)}=\frac{P_t(z_k|d_m)P_t(w_n|z_k)}{{\sum }_j{P}_t(z_j|d_m)P_t(w_n|z_j)}\end{array}$$
   基于以上两个结果，得到Q函数的形式为
   $$\begin{array}{rlr}Q(\theta ;{\theta }_t)& amp;=\sum _m\sum _{n}n(d_m,w_n)\sum _{k}P(z_k|w_n,d_m;{\theta }_t)(\ln P(z_k|d_m)+\ln & nbsp;P(w_n|z_k))\\ & amp;=\sum _m\sum _{n}n(d_m,w_n)\sum _k\frac{P_t(z_k|d_m)P_t(w_n|z_k)}{\sum _j{P}_t(z_j|d_m)P_t(w_n|z_j)}(\ln P(z_k|d_m)+\ln & nbsp;P(w_n|z_k))\end{array}$$
   终于，在这个形式里面，除了 $\theta$（全部 $K\times M$ 个 $P(z_k|d_m)$ 和 $V\times K$ 个 $P(w_n|z_k)$），已经全部为已知量。
2. M步，求极大值
   剩下的工作就是$${\theta }_{t+1}=\arg \underset{\theta }{\max }Q(\theta ;{\theta }_t)$$
   问题将会被概括为如下的约束最优化问题： 目标函数：${\max }_{\theta }Q(\theta ;{\theta }_t)$
   约束：$su{m}_{n}P(w_n|z_k)=1$，$su{m}_{k}P(z_k|d_m)=1$
   使用Lagrange乘数法，得到Lagrange函数为
   $$Q(\theta ;{\theta }_t)+\sum _k{\tau }_k(1-\sum _{n}P(w_n|z_k))+\sum _m{\rho }_m(1-\sum _{k}P(z_k|d_m))$$
   令其对参数的偏导数等于零，得到 $K\times M+V\times K$ 个方程，这些方程的解就是最优化问题的解：
   $$\frac{\partial }{\partial P(w_n|z_k)}=\frac{\sum _{m}n(d_m,w_n)P(z_k|w_n,d_m;{\theta }_t)}{P(w_n|z_k)}-{\tau }_k=0,1\le n\le V,1\le k\le K$$
   $$\frac{\partial }{\partial P(z_k|d_m)}=\frac{\sum _{n}n(d_m,w_n)P(z_k|w_n,d_m;{\theta }_t)}{P(z_k|d_m)}-{\rho }_m=0,1\le m\le M,1\le k\le K$$
   方程的解为
   $$P(w_n|z_k)=\frac{{\sum }_{m}n(d_m,w_n)P(z_k|w_n,d_m;{\theta }_t)}{{\tau }_k}$$
   $$P(z_k|d_m)=\frac{{\sum }_{n}n(d_m,w_n)P(z_k|w_n,d_m;{\theta }_t)}{{\rho }_m}$$
   注意到两个约束条件，即
   $$\sum _n\frac{{\sum }_{m}n(d_m,w_n)P(z_k|w_n,d_m;{\theta }_t)}{{\tau }_k}=1$$
   $$\sum _k\frac{{\sum }_{n}n(d_m,w_n)P(z_k|w_n,d_m;{\theta }_t)}{{\rho }_m}=1$$
   从中可求得 ${\tau }_k$ 、${\rho }_m$ ，所以方程的解为
   $$P_{t+1}(w_n|z_k)=\frac{{\sum }_{m}n(d_m,w_n)P(z_k|w_n,d_m;{\theta }_t)}{{\sum }_n{\sum }_{m}n(d_m,w_n)P(z_k|w_n,d_m;{\theta }_t)}$$
   $$P_{t+1}(z_k|d_m)=\frac{{\sum }_{n}n(d_m,w_n)P(z_k|w_n,d_m;{\theta }_t)}{{\sum }_k{\sum }_{n}n(d_m,w_n)P(z_k|w_n,d_m;{\theta }_t)}$$
   当模型参数全部估计好后，便得到了完整的 pLSA 模型。上面的迭代过程很明显是一个频数估计（极大似然估计）的形式，意义很明确。模型使用EM算法进行参数估计时往往都会推导出这样的结果，例如HMM。

LDA

我们来看看PLSA和LDA生成文档的方式。在PLSA中，生成文档的方式如下：

1. 按照概率$p(d_i)$选择一篇文档$d_i$
2. 根据选择的文档$d_i$，从从主题分布中按照概率$p({\zeta }_k\mid d_i)$选择一个隐含的主题类别${\zeta }_k$
3. 根据选择的主题${\zeta }_k$, 从词分布中按照概率$p({\omega }_j\mid {\zeta }_k)$选择一个词${\omega }_j$

LDA 中，生成文档的过程如下：

1. 按照先验概率$p(d_i)$选择一篇文档$d_i$
2. 从Dirichlet分布$\alpha$中取样生成文档$d_i$的主题分布${\theta }_i$，主题分布${\theta }_i$由超参数为$\alpha$的Dirichlet分布生成
3. 从主题的多项式分布${\theta }_i$中取样生成文档$d_i$第 j 个词的主题$z_{i,j}$
4. 从Dirichlet分布$\beta$中取样生成主题$z_{i,j}$对应的词语分布${\varphi }_{z_{i,j}}$，词语分布${\varphi }_{z_{i,j}}$由参数为$\beta$的Dirichlet分布生成
5. 从词语的多项式分布${\varphi }_{z_{i,j}}$中采样最终生成词语${\omega }_{i,j}$
   可以看出，LDA 在 PLSA 的基础上，为主题分布和词分布分别加了两个 Dirichlet 先验。
   我们来看一个例子，如图所示：
   
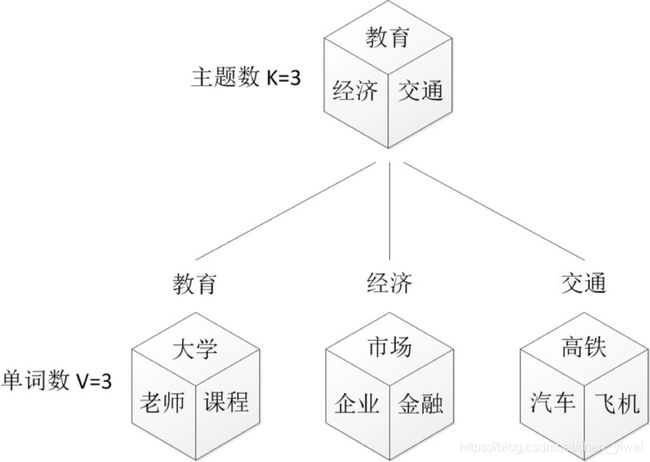
   上图中有三个主题，在PLSA中，我们会以固定的概率来抽取一个主题词，比如0.5的概率抽取教育这个主题词，然后根据抽取出来的主题词，找其对应的词分布，再根据词分布，抽取一个词汇。由此，可以看出PLSA中，主题分布和词分布都是唯一确定的。但是，在LDA中，主题分布和词分布是不确定的，LDA的作者们采用的是贝叶斯派的思想，认为它们应该服从一个分布，主题分布和词分布都是多项式分布，因为多项式分布和狄利克雷分布是共轭结构，在LDA中主题分布和词分布使用了Dirichlet分布作为它们的共轭先验分布。所以，也就有了一句广为流传的话 – LDA 就是 PLSA 的贝叶斯化版本。下面两张图片很好的体现了两者的区别：
   
   
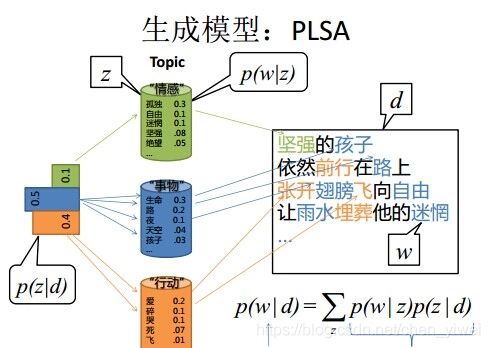
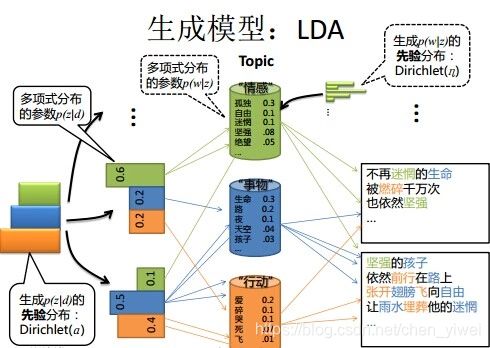
   在PLSA和LDA的两篇论文中，使用了下面的图片来解释模型，它们也很好的对比了PLSA和LDA的不同之处。
   
   
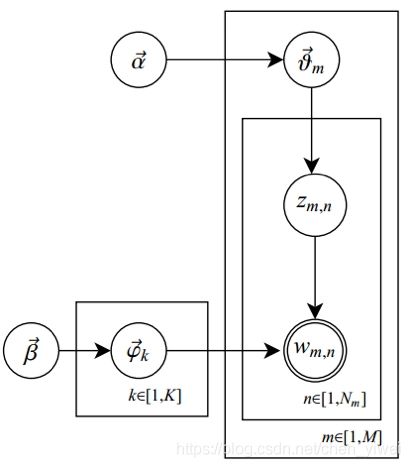
   现在我们来详细讲解论文中的LDA模型，即上图。

$\alpha \to {\theta }_m\to {\zeta }_{m,n}$, 这个过程表示在生成第m篇文档的时候，先从抽取了一个doc-topic骰子${\theta }_m$, 然后投掷这个骰子生成了文档中第n个词的topic编号${\zeta }_{m,n}$;

$\beta \to {\varphi }_k\to {\omega }_{m,n}\mid ={\zeta }_{m,n}$, 这个过程表示，从K个topic-word骰子${\varphi }_k$中，挑选编号为$k={\zeta }_{m,n}$的骰子进行投掷，然后生成词汇${\omega }_{m,n}$;

在LDA中，也是采用词袋模型，M篇文档会对应M个独立Dirichlet-Multinomial共轭结构；K个topic会对应K个独立的Dirichlet-Multinomial共轭结构。
上面的LDA的处理过程是一篇文档一篇文档的过程来处理，并不是实际的处理过程。文档中每个词的生成都要抛两次骰子，第一次抛一个doc-topic骰子得到 topic, 第二次抛一个topic-word骰子得到 word，每次生成每篇文档中的一个词的时候这两次抛骰子的动作是紧邻轮换进行的。如果语料中一共有 N 个词，则上帝一共要抛 2N次骰子，轮换的抛doc-topic骰子和 topic-word骰子。但实际上有一些抛骰子的顺序是可以交换的，我们可以等价的调整2N次抛骰子的次序：前N次只抛doc-topic骰子得到语料中所有词的 topics,然后基于得到的每个词的 topic 编号，后N次只抛topic-word骰子生成 N 个word。此时，可以得到：
$$\begin{array}{rl}p(w,z\mid \alpha ,\beta )& =p(w\mid z,\beta )p(z\mid \alpha )\\ & =\prod _{k=1}^K\frac{\Delta ({\varphi }_K+\beta )}{\Delta (\beta )}\prod _{m=1}^M\frac{\Delta ({\theta }_m+\alpha )}{\alpha }\end{array}$$

Gibbs Sampling

根据上一小节中的联合概率分布$p(\omega ,z)$, 我们可以使用Gibbs Sampling对其进行采样。
语料库$z$中的第i个词我们记为$z_i$, 其中i=(m,n)是一个二维下标，对应于第m篇文档的第n个词，用$\neg i$ 表示去除下标为i的词。根据第二小节中的Gibbs Sampling 算法，我们需要求任一个坐标轴 i 对应的条件分布 $p(z_i=k|z_{\neg i},\omega )$ 。假设已经观测到的词 ${\omega }_i=t$, 则由贝叶斯法则，我们容易得到:
$$\begin{array}{rl}p(z_i=k\mid z_{\neg i},\omega )& amp;\propto p(z_i=k,{\omega }_i=t\mid z_{\neg i},{\omega }_{\neg i})\end{array}$$
由于$z_i=k,w_i=t$ 只涉及到第 m 篇文档和第k个 topic，所以上式的条件概率计算中, 实际上也只会涉及到与之相关的两个Dirichlet-Multinomial 共轭结构，其它的 M+K−2 个 Dirichlet-Multinomial 共轭结构和$z_i=k,w_i=t$是独立的。去掉一个词汇，并不会改变M + K 个Dirichlet-Multinomial共轭结构，只是某些地方的计数减少而已。于是有：
$$\begin{array}{rl}p({\theta }_m\mid z_{\neg i},{\omega }_{\neg i})& amp;=Dir({\theta }_m\mid n_{m,\neg i}+\alpha )\\ p({\phi }_k\mid z_{\neg i},{\omega }_{\neg i})& amp;=Dir({\phi }_k\mid n_{k,\neg i}+\beta )\end{array}$$
下面进行本篇文章最终的核心数学公式推导：
$$\begin{array}{rl}p(z_i=k\mid z_{\neg i},\omega )& amp;\propto p(z_i=k,{\omega }_i=t\mid z_{\neg i},{\omega }_{\neg i})\\ & =\int p(z_i=k,{\omega }_i=t,{\theta }_m,{\phi }_k\mid z_{\neg i},{\omega }_{\neg i})d{\theta }_{m}d{\phi }_k\\ & =\int p(z_i=k,{\theta }_m,\mid z_{\neg i},{\omega }_{\neg i})\cdot p({\omega }_i=t,{\phi }_k,\mid z_{\neg i},{\omega }_{\neg i})d{\theta }_{m}d{\phi }_k\\ & =\int p(z_i=k\mid {\theta }_m)p({\theta }_m\mid z_{\neg i},{\omega }_{\neg i})\cdot p({\omega }_i=t\mid {\phi }_k)p({\phi }_k\mid z_{\neg i},{\omega }_{\neg i})d{\theta }_{m}d{\phi }_k\\ & =\int p(z_i=k\mid {\theta }_m)Dir({\theta }_m\mid n_{m,\neg i}+\alpha )d{\theta }_m\cdot p({\omega }_i=t\mid {\phi }_k)Dir({\phi }_k\mid n_{k,\neg i}+\beta )d{\phi }_k\\ & =\int {\theta }_{mk}Dir({\theta }_m\mid n_{m,\neg i}+\alpha )d{\theta }_m\cdot \int {\phi }_{kt}Dir({\phi }_k\mid n_{k,\neg i}+\beta )d{\phi }_k\\ & =E({\theta }_{mk})\cdot E({\phi }_{kt})\\ & ={\hat{\theta }}_{mk}\cdot {\hat{\phi }}_{kt}\end{array}$$
最终得到的 ${\hat{\theta }}_{mk}\cdot {\hat{\phi }}_{kt}$ 就是对应的两个 Dirichlet 后验分布在贝叶斯框架下的参数估计。借助于前面介绍的Dirichlet 参数估计的公式 ，有:
$$\begin{array}{rl}{\hat{\theta }}_{mk}& amp;=\frac{n_{m,\neg i}^{(k)}+{\alpha }_k}{{\sum }_{k=1}^K(n_{m,\neg i}^{(k)}+{\alpha }_k)}\\ {\hat{\phi }}_{kt}& amp;=\frac{n_{k,\neg i}^{(t)}+{\beta }_t}{{\sum }_{t=1}^V(n_{k,\neg i}^{(t)}+{\beta }_t)}\end{array}$$
最终，我们得到LDA 模型的 Gibbs Sampling 公式为：
$$\begin{array}{r}p(z_i=k|{\mathbf{z}}_{\neg i},\mathbf{w})\propto \frac{n_{m,\neg i}^{(k)}+{\alpha }_k}{{\sum }_{k=1}^K(n_{m,\neg i}^{(k)}+{\alpha }_k)}\cdot \frac{n_{k,\neg i}^{(t)}+{\beta }_t}{{\sum }_{t=1}^V(n_{k,\neg i}^{(t)}+{\beta }_t)}\end{array}$$

LDA Training

根据上一小节中的公式，我们的目标有两个：

1. 估计模型中的参数 ${\phi }_1,\cdots ,{\phi }_K$ 和 ${\theta }_1,\cdots ,{\theta }_M$;
2. 对于新来的一篇文档，我们能够计算这篇文档的 topic 分布$\theta$。
   训练的过程：
3. 对语料库中的每篇文档中的每个词汇$\omega$，随机的赋予一个topic编号z
4. 重新扫描语料库，对每个词$\omega$，使用Gibbs Sampling公式对其采样，求出它的topic，在语料中更新
5. 重复步骤2，直到Gibbs Sampling收敛
6. 统计语料库的topic-word共现频率矩阵，该矩阵就是LDA的模型；
   根据这个topic-word频率矩阵，我们可以计算每一个p(word|topic)概率，从而算出模型参数${\phi }_1,\cdots ,{\phi }_K$, 这就是那 K 个 topic-word 骰子。而语料库中的文档对应的骰子参数 ${\theta }_1,\cdots ,{\theta }_M$ 在以上训练过程中也是可以计算出来的，只要在 Gibbs Sampling 收敛之后，统计每篇文档中的 topic 的频率分布，我们就可以计算每一个 p(topic|doc) 概率，于是就可以计算出每一个${\theta }_m$。由于参数${\theta }_m$ 是和训练语料中的每篇文档相关的，对于我们理解新的文档并无用处，所以工程上最终存储 LDA 模型时候一般没有必要保留。通常，在 LDA 模型训练的过程中，我们是取 Gibbs Sampling 收敛之后的 n 个迭代的结果进行平均来做参数估计，这样模型质量更高。

LDA Inference

有了 LDA 的模型，对于新来的文档 doc, 我们只要认为 Gibbs Sampling 公式中的 ${\phi }_{kt}$ 部分是稳定不变的，是由训练语料得到的模型提供的，所以采样过程中我们只要估计该文档的 topic 分布$\theta$就好了. 具体算法如下：

1. 对当前文档中的每个单词$\omega$, 随机初始化一个topic编号z;
2. 使用Gibbs Sampling公式，对每个词$\omega$, 重新采样其topic；
3. 重复以上过程，知道Gibbs Sampling收敛；
4. 统计文档中的topic分布，该分布就是$\theta$
   Tips

懂 LDA 的面试官通常会询问求职者，LDA 中主题数目如何确定？

在 LDA 中，主题的数目没有一个固定的最优解。模型训练时，需要事先设置主题数，训练人员需要根据训练出来的结果，手动调参，有优化主题数目，进而优化文本分类结果。

LDA实践

修改之前 SVM与贝叶斯分类中提取特征的部分即可

from scipy.sparse import hstack
def tf_LDA_deal_cnews(input_file_name,out_file_name):
    bunch=_read_bunch(input_file_name)#读取数据
    stop_words=get_stop_words()#得到停用词
    #实例化bunch对象
    #tmd（权重列表）
    #vocabulary（词典索引）
    space_bunch=Bunch(targets=bunch.targets,filename=bunch.filenames,labels=bunch.labels,tmd=[],vocabulary={
     })
    #使用特征提取函数TfidfVectorizer初始化向量空间模型
    tf_vector=TfidfVectorizer(stop_words=stop_words,sublinear_tf=True,max_df=0.5,max_features=10000)#提取函数的初始化，啥数据都没有处理。选择能代表新闻特征、独一无二的词汇，词频大于50%的就被过滤掉？？？如果过大、过小会如何？
    
    tf_features=tf_vector.fit_transform(bunch.contents)
    ## lda
    lda = LatentDirichletAllocation(n_topics=10, max_iter=5,
                                learning_method='online',
                                learning_offset=50.,
                                random_state=0)
    cnt_vector =CountVectorizer(stop_words=stop_words,max_df=0.5,max_features=10000)
    cntTf = cnt_vector.fit_transform(bunch.contents)
    LDA_features = lda.fit_transform(cntTf)
    
    
    
    print(tf_features.shape)
    print(LDA_features.shape)
    space_bunch.tmd= hstack((tf_features,LDA_features))
    print(space_bunch.tmd.shape)
    space_bunch.vocabulary=tf_vector.vocabulary_#词典索引，统计词频
    '''
    print(space_bunch.vocabulary)输出格式如下：
    {'黄蜂': 834, 'vs': 38, '湖人': 557, '首发': 820, '科比': 609, '带伤': 352, '保罗': 156,
    '''
    _write_bunch(space_bunch,out_file_name)#写入文件

参考链接

pLSA模型
一文详解LDA主题模型