LeetCode刷题笔记（Java）---第321-340题

前言

需要开通vip的题目暂时跳过

笔记导航

点击链接可跳转到所有刷题笔记的导航链接

321. 拼接最大数

给定长度分别为 m 和 n 的两个数组，其元素由 0-9 构成，表示两个自然数各位上的数字。现在从这两个数组中选出 k (k <= m + n) 个数字拼接成一个新的数，要求从同一个数组中取出的数字保持其在原数组中的相对顺序。

求满足该条件的最大数。结果返回一个表示该最大数的长度为 k 的数组。

说明: 请尽可能地优化你算法的时间和空间复杂度。

• 解答

    public int[] maxNumber(int[] nums1, int[] nums2, int k) {
     
        int[] res = new int[k];
        for (int i = 0; i <= k; i++) {
     
            int j = k - i;
            if (i > nums1.length || j > nums2.length) continue;
            int[] max1 = findMax(nums1, nums1.length - i);
            int[] max2 = findMax(nums2, nums2.length - j);
            int[] temp = merge(max1, max2);
            res = compare(res, 0, temp, 0) ? res : temp;
        }
        return res;
    }

    public int[] findMax(int[] nums, int k) {
     //删除k个使得数字最大
        if (k == nums.length) return new int[0];
        int number = 0;
        Stack<Integer> stack = new Stack<>();
        stack.add(nums[0]);
        for (int i = 1; i < nums.length; i++) {
     
            while (!stack.isEmpty() && number < k) {
     
                int top = stack.peek();
                if (nums[i] > top) {
     
                    stack.pop();
                    number++;
                } else break;
            }
            stack.add(nums[i]);
        }
        while(number < k){
     
            stack.pop();
            number++;
        }
        int[] res = new int[stack.size()];
        int index = res.length - 1;
        while (!stack.isEmpty())
            res[index--] = stack.pop();
        return res;
    }

    public int[] merge(int[] nums1, int[] nums2) {
     //合并
        int[] res = new int[nums1.length + nums2.length];
        int index1 = 0;
        int index2 = 0;
        int index = 0;
        while ((index1 < nums1.length || index2 < nums2.length) && index < res.length) {
     
            if (index1 == nums1.length) {
     
                while (index2 < nums2.length && index < res.length) res[index++] = nums2[index2++];
            } else if (index2 == nums2.length) {
     
                while (index1 < nums1.length && index < res.length) res[index++] = nums1[index1++];
            } else {
     
                if (nums1[index1] < nums2[index2]) res[index++] = nums2[index2++];
                else if (nums1[index1] > nums2[index2]) res[index++] = nums1[index1++];
                else {
     
                    if (compare(nums1, index1, nums2, index2)) res[index++] = nums1[index1++];
                    else res[index++] = nums2[index2++];
                }
            }
        }
        return res;
    }

    public boolean compare(int[] nums1, int index1, int[] nums2, int index2) {
     //比较
        while (index1 < nums1.length && index2 < nums2.length) {
     
            if (nums1[index1] > nums2[index2]) return true;
            else if (nums1[index1] < nums2[index2]) return false;
            index1++;
            index2++;
        }
        if (index1 < nums1.length) return true;
        else return false;
    }

• 分析

  1. 两个数组选出k个构成最大数字。并且选择的同一数组中的数字保持有序。可以将问题拆分成从数组1中选择一个m个数字组成的最大数字和数字2中选择一个n个数字组成的最大数字。确保m+n = k。分治的思想。拆分成子问题。
  2. 子问题就是如何从一个数组中得到m个数字组成的最大值。
  3. 选出m个数字 实际就是删除数组长度-m个数字。记为n。
  4. 子问题就变成了给定数组中删除n个数字 使得剩余的数字构成的数最大。
  5. 第一个数字入栈。从第二个位置开始遍历数组。每次判断栈顶数字是否小于当前遍历的数字。如果小于，则将栈顶出栈。表示删除这个数字，记录删除个数。因为先入栈的是高位。数字高位越大表示数字也越大。所以小的删掉。当删除个数达到n的时候其余的数字不再删除。还有一种情况就是 遍历完了数组。当前删除的个数还不到n个。则从栈顶再删去，直到删掉n个数字。此时在栈中的数字所组成的就是删除n个数字后可以得到的最大值。
  6. 好了 子问题求解完毕了。得到了两个数组中分别的最大值。如何将这两者合并得到最大值是接下来要解决的问题。
  7. 同时遍历两个数组，选择数字更大的作为当前位。若数字一样，则比较后续的数字组合哪个更大。选择大的作为当前位。这样就可以得到两个数组组合成一个最大的值。
  8. 求解完所有的子问题 就可以得到原问题的答案。

• 提交结果
  

322. 零钱兑换

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

• 解答

  	int res3 = Integer.MAX_VALUE;
  
      public int coinChange(int[] coins, int amount) {
         
          Arrays.sort(coins);
          dfs(coins, amount, 0, coins.length - 1);
          return res3 == Integer.MAX_VALUE ? -1 : res3;
      }
  
      public void dfs(int[] coins, int amount, int number, int index) {
         
          if (amount == 0) {
         
              res3 = Math.min(res3, number);
              return;
          }
          if (index < 0) return;
          int n = amount / coins[index];
          for (int i = n; i >= 0 && number + i < res3; i--) {
         
              dfs(coins, amount - coins[index] * i, number + i, index - 1);
          }
      }
  

• 分析

  1. 一开始按部就班的一个一个的硬币取的dfs会超时
  2. 所以索性一次性取n个硬币。n等于当前的金额除以当前硬币的面值。就是指这个硬币的个数。
  3. 金额减去拿的硬币的总价值，计数number加上拿的硬币数。index表示选择的硬币面值，进入下一层递归index-1。
  4. 一开始硬币先排好序。先从面值高的开始拿。
  5. 当金额等于0的时候。 计算当前硬币的数量，和已记录最小值比较 保留更小者。
  6. 若剩余的金额无法通过拿硬币归0，那么就回溯。拿n-1个硬币。
  7. 剪枝。当前拿的硬币数量大于已记录的硬币数量 则不再递归。

• 提交结果
  

324.摆动排序 II

给定一个无序的数组 nums，将它重新排列成 nums[0] < nums[1] > nums[2] < nums[3]… 的顺序。

• 解答

	int n=-1;
    public void wiggleSort(int[] nums) {
     
        //找到中位数索引
        int midIndex = this.quickSelect(nums,0,nums.length-1);
        //找到中位数
        int mid = nums[midIndex];
        n=nums.length;
        //三分法
        for(int i=0,j=0,k=nums.length-1;j<=k;){
     
            if(nums[V(j)]>mid){
     
                swap(nums,V(j++),V(i++));
            }else if(nums[V(j)]<mid){
     
                swap(nums,V(j),V(k--));
            }else{
     
                j++;
            }
        }
    }
    
    public int V(int i){
     
        return (1+2*(i)) % (n|1);
    }
    
    public void swap(int[] nums,int i,int j){
     
        int t = nums[i];
        nums[i]=nums[j];
        nums[j]=t;
    }
    
    public int quickSelect(int[] nums,int left,int right){
     
        int pivot = nums[left];
        int l = left;
        int r = right;
        while(l<r){
     
            while(l<r&&nums[r]>=pivot){
     
                r--;
            }
            if(l<r){
     
                nums[l++]=nums[r];
            }
            while(l<r&&nums[l]<=pivot){
     
                l++;
            }
            if(l<r){
     
                nums[r--]=nums[l];
            }
        }
        nums[l]=pivot;
        if(l==nums.length/2){
     
            return l;
        }else if(l>nums.length/2){
     
            return this.quickSelect(nums,left,l-1);
        }else{
     
            return this.quickSelect(nums,l+1,right);
        }
    }

• 分析

  1. 一大一小数字穿插
  2. 所以可以使用中位数，将数组分成两堆，然后将两堆数字进行穿插的排列。
  3. 寻找中位数使用快速选择排序。相比于快速排序要递归两侧，快速选择排序只需要递归一侧即可。时间复杂度更低。
  4. 找到中位数后，左边的小于等于中位数，右边的大于等于中位数。
  5. 利用三分法进行数字的交换。

• 提交结果
  

326. 3的幂

给定一个整数，写一个函数来判断它是否是 3 的幂次方。

• 解答

		//方法一
    public boolean isPowerOfThree(int n) {
     
        return Integer.toString(n, 3).matches("^10*$");
    }
		//方法二
	public boolean isPowerOfThree(int n) {
     
        return n > 0 && 1162261467 % n == 0;
    }
		

• 分析

  1. 方法一 将n转换成3进制。当三进制数的首位为1 后面全是0的时候 就是3的幂
  2. n是int类型 所以最大的3的幂是1162261467，而3是质数，所以1162261467整除的数，就是3的幂

• 提交结果

  方法一

  方法二

327.区间和的个数

给定一个整数数组 nums，返回区间和在 [lower, upper] 之间的个数，包含 lower 和 upper。
区间和 S(i, j) 表示在 nums 中，位置从 i 到 j 的元素之和，包含 i 和 j (i ≤ j)。

• 解答

  	public int countRangeSum(int[] nums, int lower, int upper) {
         
          if(nums ==  null || nums.length == 0){
         
              return 0;
          }
          //键值为区间和和这个区间和出现的次数
          TreeMap<Long, Integer> tree = new TreeMap<>();
          tree.put(0L, 1);
          
          int count = 0;
          long sum = 0L;
          for(int num : nums){
         
              sum += num;
              //subMap()返回一个值在sum - upper 和sum - lower 之间的子集合，values()方法获得这个映射的值得视图
              for(int cnt : tree.subMap(sum - upper, true, sum - lower, true).values()){
         
                  count += cnt; //统计满足条件的区间和个数
              }
              tree.put(sum, tree.getOrDefault(sum, 0) + 1);
          }
          return count;
      }
  

• 分析

  1. 区间和的第一反应是使用前缀和来计算。sum[j] - sum[i] 来表示i-j的区间和
  2. 题目要求求区间和在给定范围内的个数 即满足lower <=sum[j] - sum[i]<=upper
  3. 变换下公式可得到 sum[j] - upper <= sum[i] <= sum[j] - lower
  4. 所以题目就变成了 给定sum[j] 、upper、lower 那么在上述范围内满足的sum[i]的个数有多少个
  5. 代码中的sum就等于这里的sum[j]
  6. TreeMap底层是红黑树。查找的时间复杂度为O(logN)。一边计算前缀和 一遍插入到树中。
  7. subMap()返回一个值在sum - upper 和sum - lower 之间的子集合 可以得到满足这个前缀和范围内的个数是多少。然后统计下来。
  8. tree.put(sum, tree.getOrDefault(sum, 0) + 1); 将前缀和和出现的次数+1

• 提交结果
  

328.奇偶链表

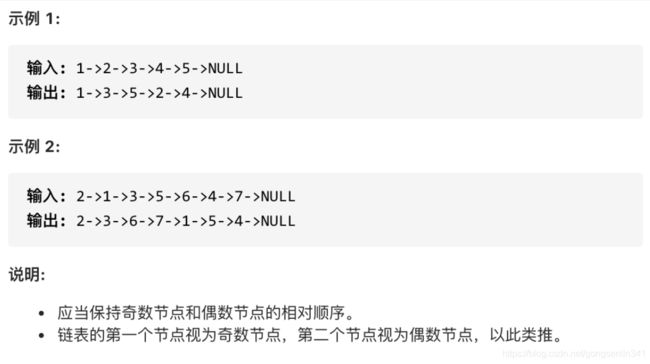
给定一个单链表，把所有的奇数节点和偶数节点分别排在一起。请注意，这里的奇数节点和偶数节点指的是节点编号的奇偶性，而不是节点的值的奇偶性。

请尝试使用原地算法完成。你的算法的空间复杂度应为 O(1)，时间复杂度应为 O(nodes)，nodes 为节点总数。

• 解答

	public ListNode oddEvenList(ListNode head) {
     
        if(head == null || head.next == null)return head;
        ListNode odd = head;
        ListNode even = head.next;
        ListNode evenFirst = even;
        while(even.next !=null){
     
            odd.next = even.next;
            odd = even.next;
            if(odd.next!=null){
     
                even.next = odd.next;
                even = odd.next;
            }else even.next = null;
        }
        odd.next = evenFirst;
        return head;
    }

• 分析

  1. 三个指针 一个是指向奇数结点 一个指向偶数结点 一个指向偶数结点的第一个。
  2. while循环，将奇数结点相连，偶数结点相连。最后奇数结点的最后一个的后继指向最开始记录的第一个偶数结点即可。

• 提交结果
  

329.矩阵中的最长递增路径

给定一个整数矩阵，找出最长递增路径的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 你不能在对角线方向上移动或移动到边界外（即不允许环绕）。

• 解答

	int[][] points = {
     {
     1,0},{
     -1,0},{
     0,1},{
     0,-1}};
    public int longestIncreasingPath(int[][] matrix) {
     
        if(matrix == null || matrix.length==0 || matrix[0].length==0)return 0;
        int row = matrix.length;
        int column = matrix[0].length;
        int[][] dp = new int[row][column];
        int max = 0;
        for(int i = 0;i<row;i++){
     
            for(int j = 0;j<column;j++){
     
                max = Math.max(max,dfs(matrix,i,j,dp));
            }
        }
        return max;
    }

    public int dfs(int[][] matrix,int row,int column,int[][] dp){
     
        if(dp[row][column] != 0)
            return dp[row][column];
        ++dp[row][column];
        for(int[] point:points){
     
            int newRow = row+point[0];
            int newColumn = column+point[1];
            if(newRow>=0 && newRow < matrix.length && newColumn >= 0 && newColumn < matrix[0].length && matrix[newRow][newColumn] > matrix[row][column])
                dp[row][column] = Math.max(dp[row][column],dfs(matrix,newRow,newColumn,dp)+1);
        }
        return dp[row][column];
    }

• 分析
  1. 纯dfs做的话会超时
  2. 所以这里就引入了dp数组来保留已经计算出的最长路径。避免重复计算。
• 提交结果

330. 按要求补齐数组

给定一个已排序的正整数数组 nums，和一个正整数 n 。从 [1, n] 区间内选取任意个数字补充到 nums 中，使得 [1, n] 区间内的任何数字都可以用 nums 中某几个数字的和来表示。请输出满足上述要求的最少需要补充的数字个数。

• 解答

  	public int minPatches(int[] nums, int n) {
         
          int res = 0, i = 0;
          long miss = 1;
          while (miss <= n) {
         
              if (i < nums.length && nums[i] <= miss)
                  miss += nums[i++];
              else {
         
                  miss += miss;
                  res++;
              }
          }
          return res;
      }
  

• 分析

  1. 举例说明吧，假设nums 表示[1,5,10] 一个指针i指向数组的第一个数字 此时是1.
  2. 缺少的数字从1开始判断。
  3. 若当前指针指向的数字小于等于缺少的数字。则将缺少的数字加上当前指针指向的数字 miss为2，指针后移一位。
  4. 继续判断。此时指针所指向的数字是5 miss为2 小于5，那么就说明找到了一个缺少的数字。res+1。 并且可以发现miss之前的数字都是可以组成的，所以2*miss-1 的数字是肯定可以得到的。此时miss修改为2倍的miss 为4
  5. 同理 4也小于5。 res+1， 1-4 同理 2* 4 -1的数字是肯定可以得到的。此时miss 修改为2倍的miss 为8.
  6. 8 > 5。 miss+5 = 13 大于10 结束循环。
  7. 可知找到了2个需要填充的数字。

• 提交结果
  

331.验证二叉树的前序序列化

序列化二叉树的一种方法是使用前序遍历。当我们遇到一个非空节点时，我们可以记录下这个节点的值。如果它是一个空节点，我们可以使用一个标记值记录，例如 #。

例如，上面的二叉树可以被序列化为字符串 “9,3,4,#,#,1,#,#,2,#,6,#,#”，其中 # 代表一个空节点。

给定一串以逗号分隔的序列，验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。

每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 ‘#’ 。

你可以认为输入格式总是有效的，例如它永远不会包含两个连续的逗号，比如 “1,3” 。

• 解答

      public boolean isValidSerialization(String preorder) {
         
          int slotNumber = 1;
          String[] points = preorder.split(",");
          for(String point: points){
         
              slotNumber--;
              if(slotNumber < 0)return false;
              if(!"#".equals(point))
                  slotNumber+=2;
          }
          return slotNumber == 0;
      }
  

• 分析

  1. 从头遍历给定的序列。若出现的是数字，那么必定有两个孩子结点。若出现的是“#”，那么它就是叶子节点。
  2. 所以根据以上的规则，可以设定槽的数量，来容纳遍历过的结点。一开始槽的数量是1，若出现数字，则槽的数量+2。每遍历一个结点都要消耗一个槽位。槽位要减1.
  3. 如果在遍历的过程中，槽位的数量小于0了。说明出现了太多的叶子节点，不符合二叉树，返回false。
  4. 最后遍历完了，看槽位是否等于0.如果等于0的话，说明是一个正确的二叉树的先序序列。否则不是。

• 提交结果
  

332. 重新安排行程

给定一个机票的字符串二维数组 [from, to]，子数组中的两个成员分别表示飞机出发和降落的机场地点，对该行程进行重新规划排序。所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。

提示：

1. 如果存在多种有效的行程，请你按字符自然排序返回最小的行程组合。例如，行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小，排序更靠前
2. 所有的机场都用三个大写字母表示（机场代码）。
3. 假定所有机票至少存在一种合理的行程。
4. 所有的机票必须都用一次 且 只能用一次。

• 解答

	public List<String> findItinerary(List<List<String>> tickets) {
     
        List<String> ans = new LinkedList<>();
        if (tickets == null || tickets.size() == 0)
            return ans;
        Map<String, PriorityQueue<String>> graph = new HashMap<>();
        for (List<String> pair : tickets) {
     
            PriorityQueue<String> nbr = graph.computeIfAbsent(pair.get(0), k -> new PriorityQueue<>());
            nbr.add(pair.get(1));
        }
        visit(graph, "JFK", ans);
        return ans;
    }
    // DFS方式遍历图，当走到不能走为止，再将节点加入到答案
    private void visit(Map<String, PriorityQueue<String>> graph, String src, List<String> ans) {
     
        PriorityQueue<String> nbr = graph.get(src);
        while (nbr != null && nbr.size() > 0) {
      // 有邻居 递归
            String dest = nbr.poll();//出队 因为是优先队列 每次取出的都是字典序最小的值
            visit(graph, dest, ans);
        }
        ans.add(0, src); // 没有邻居了 逆序插入
    }

• 分析

  1. 一张图走遍所有的路径且路径不重复使用，遍历过的路径叫做欧拉路径，可以理解为用一笔将所有的线描一遍。
  2. 求欧拉路径可以使用hierholzer算法
     1. 任选一个点为起点（题目把起点告诉你了），遍历它所有邻接的边（设置不同的分支）。
     2. DFS 搜索，访问邻接的点，并且将走过的边（邻接关系）删除。也就是出队了。
     3. 如果走到的当前点，已经没有相邻边了，则将当前点推入 res。
     4. 随着递归的出栈，点不断推入 res 的开头（逆序插入），最后就得到一个从起点出发的欧拉路径。
  3. 而且此题要求最小字典序答案。那么有向图的邻接表就用优先队列来存储。这样每次出队的节点都是当前节点所以可以到达的字典序最小的节点。然后就按照hierholzer算法来实现即可。

• 提交结果
  

334. 递增的三元子序列

给定一个未排序的数组，判断这个数组中是否存在长度为 3 的递增子序列。

数学表达式如下:

如果存在这样的 i, j, k, 且满足 0 ≤ i < j < k ≤ n-1，
使得 arr[i] < arr[j] < arr[k] ，返回 true ; 否则返回 false 。
说明: 要求算法的时间复杂度为 O(n)，空间复杂度为 O(1) 。

• 解答

  // 方法一
  	public boolean increasingTriplet(int[] nums) {
         
          if(nums.length < 3)return false;
          List<Integer> list = new ArrayList<>();
          list.add(nums[0]);
          for (int i = 1; i < nums.length; i++) {
         
              if (nums[i] > list.get(list.size() - 1)) {
         
                  list.add(nums[i]);
                  if (list.size() == 3) return true;
              } else {
         
                  for (int j = 0; j < list.size(); j++) {
         
                      if (list.get(j) == nums[i])
                          break;
                      if (list.get(j) > nums[i]) {
         
                          list.set(j, nums[i]);
                          break;
                      }
                  }
              }
          }
          return false;
      }
  // 方法二
  	public boolean increasingTriplet(int[] nums) {
         
          int min = Integer.MAX_VALUE;
          int second = Integer.MAX_VALUE;
          for(int i = 0;i<nums.length;i++){
         
              if(nums[i] == min || nums[i] == second){
         
                  continue;
              }
              else if(nums[i] < min){
         
                  min = nums[i];
              }else if(nums[i] < second){
         
                  second  = nums[i];
              }else if(nums[i] > second)return true;
          }
          return false;
      }
  

• 分析

  ​ 方法一

  1. 遍历一遍nums数组。当前数字大于list中的最后一个数字，则将这个数字加入到list中。
  2. 否则就替换掉第一个比它大的数字。
  3. 若这个数字已存在list中，则不进行替换。替换掉第一个比它大的数字并不会影响统计递增子序列的个数。
  4. 为的是缩小递增子序列中元素的值，以寻找更长的递增子序列。

  ​ 方法二

  1. 观察上面的方法，可以发现当list中有3个值的时候，就返回true。也就是当出现一个数字比第二个数字大的时候，返回true。
  2. 所以并不需要list来存储，只需要两个遍历来存储最小和第二小的即可。
  3. 初始化变量min 和second为Integer的最大值。
  4. 遍历nums数组。若出现一样的数字跳过。否则先和min比较，若比min小，则替换它，否则和second比较，若比second小则替换second，若比second大，则说明找到了长度为3的递增子序列返回true。

• 提交结果

  方法一

  

  方法二

  

335.路径交叉

给定一个含有 n 个正数的数组 x。从点 (0,0) 开始，先向北移动 x[0] 米，然后向西移动 x[1] 米，向南移动 x[2] 米，向东移动 x[3] 米，持续移动。也就是说，每次移动后你的方位会发生逆时针变化。

编写一个 O(1) 空间复杂度的一趟扫描算法，判断你所经过的路径是否相交。

• 解答

  	public boolean isSelfCrossing(int[] x) {
         
          if(x.length < 4)return false;
          if(x[2] <= x[0] && x[3] >= x[1])return true;
          if(x.length > 4 && x[3] <= x[1] && x[4] >= x[2])return true;
          if(x.length > 4 && x[3] == x[1] && x[4] + x[0] >= x[2])return true;
          for(int i = 5;i < x.length;i++){
         
              if(x[i-1] <= x[i-3] && x[i] >= x[i-2])return true;
              if(x[i-1] <= x[i-3] && x[i-4] <= x[i-2] && x[i] + x[i-4] >= x[i-2] && x[i-5] + x[i-1] >= x[i-3])return true;
          }
          return false;
      }
  

• 分析

  1. 先把可能相交的结果画出来，可以得到以下的结论
  2. 第一个if x数组长度小于4的时候 必定是不会相交的 返回false。
  3. 第二个if 当x数组长度等于4的时候，仅有一种情况会导致相交。第三条条边小于等于第一条边，第四条边大于等于第二条边的时候，返回true。
  4. 第三个if 当长度大于4的时候，且考虑前5条边5。当第四条边小于等于第二条边 并且 最后一条边大于等于第三条边的时候，返回true。
  5. 第四个if 当长度大于4的时候，且考虑前5条边5。第四条边等于第二条边 并且最后一条边的长度加上第一条边的长度大于等于第三条边长度的时候，返回true。
  6. 当线段数量大于等于5开始，就有规律了。如for循环内的条件一样。

• 提交结果
  

336.回文对

给定一组 互不相同 的单词， 找出所有不同 的索引对(i, j)，使得列表中的两个单词， words[i] + words[j] ，可拼接成回文串。

• 解答

     class Node{
         
          int[] ch = new int[26];
          int flag;
          public Node(){
         
              flag = -1;
          }
      }
      List<Node> tree = new ArrayList<>();
  
      public List<List<Integer>> palindromePairs(String[] words) {
         
          tree.add(new Node());
          for(int i = 0;i<words.length;i++){
         //将单词插入前缀树中，并在最后一个字母处标记好属于第几个单词。
              insert(words[i],i);
          }
          List<List<Integer>> res = new ArrayList<>();
          for(int i = 0;i<words.length;i++){
         //遍历words数组
              int len = words[i].length();
              for(int j = 0;j<=len;j++){
         //遍历分割点
                  if(j != 0 && isPalindrome(words[i],0,j-1)){
         //若 0 ～ j-1是回文字符串，那么就去寻找有没有 j～len-1字符串的逆序字符串，可拼接成回文字符串。
                      int leftIndex = findWord(words[i],j,len-1);
                      if(leftIndex != - 1 && leftIndex != i){
         
                          res.add(Arrays.asList(leftIndex,i));
                      }
                  }
                  if(isPalindrome(words[i],j,len-1)){
         //若 j～len-1 是回文字符串，那么就寻找有没有0～j-1字符串的逆序字符串，可拼接成回文字符串。
                      int rightIndex = findWord(words[i],0,j-1);
                      if(rightIndex != -1 && rightIndex != i){
         
                          res.add(Arrays.asList(i,rightIndex));
                      }
                  }
              }
          }
          return res;
      }
  		
  		// 插入前缀树
      public void insert(String str,int index){
         
          int add = 0;
          for(int i = 0;i<str.length();i++){
         
              int x = str.charAt(i) - 'a';
              if(tree.get(add).ch[x] == 0){
         
                  tree.add(new Node());
                  tree.get(add).ch[x] = tree.size()-1;
              }
              add = tree.get(add).ch[x];
          }
          tree.get(add).flag = index;
      }
  		// 判断字符串是否回文
      public boolean isPalindrome(String str,int start,int end){
         
          int len = end - start + 1;
          for(int i = 0;i < len/2;i++){
         
              if(str.charAt(start + i) != str.charAt(end-i))
                  return false;
          }
          return true;
      }
  		//寻找前缀树中匹配的字符串。 返回下标
      public int findWord(String str,int left,int right){
         
          int add = 0;
          for(int i = right;i>= left;i--){
         
              int index = str.charAt(i) - 'a';
              if(tree.get(add).ch[index] == 0)
                  return -1;
              add = tree.get(add).ch[index];
          }
          return tree.get(add).flag;
      }
  

• 分析

  1. 两个字符串x和y组合能否组成一个回文字符串的情况有以下三种：
     1. x和y长度相等，且x的逆序和y相同
     2. x的长度大于y，那么x分为两部分，一部分是回文字符串，另一部分和y的逆序相同
     3. y的长度大于x，那么y分为两部分，一部分是回文字符串，另一部分和x的逆序相同。
  2. 首先构建前缀树，用前缀树来保存遍历过的字符串。并且在最后一个字母的节点标记属于第几个字符串。
  3. 遍历words字符串。然后遍历字符串中的每一位，选择一个作为分割点，若分割点前一部分是回文字符串，则去前缀树中去寻找分割点后一部分的字符串是否存在（逆序的遍历）,若存在会返回找到的字符串的下标。若找到了匹配的字符串，则记录下来。
  4. 同理，分割点后一部分是回文字符串，则去前缀树中去寻找分割点前一部分的字符串是否存在（逆序的遍历），若存在会返回找到的字符串的下标。记录下来。

• 提交结果
  

337.打家劫舍 III

在上次打劫完一条街道之后和一圈房屋后，小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为“根”。 除了“根”之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫，房屋将自动报警。

计算在不触动警报的情况下，小偷一晚能够盗取的最高金额。

• 解答

  		// 方法一
  		Map<TreeNode,Integer> rob = new HashMap<>();
      Map<TreeNode,Integer> notRob = new HashMap<>();
      public int rob(TreeNode root) {
         
          if(root == null) return 0;
          dfs(root);
          return Math.max(rob.get(root),notRob.get(root));
      }
  
      public void dfs(TreeNode root){
         
          if(root == null)return;
          dfs(root.left);
          dfs(root.right);
          rob.put(root,root.val + notRob.getOrDefault(root.left,0) + notRob.getOrDefault(root.right,0));
          notRob.put(root,Math.max(notRob.getOrDefault(root.left,0),rob.getOrDefault(root.left,0))+ Math.max(notRob.getOrDefault(root.right,0),rob.getOrDefault(root.right,0)));
      }
  		// 方法二
  		public int rob(TreeNode root) {
         
          if(root == null) return 0;
          int[] rootStatus = dfs(root);
          return Math.max(rootStatus[0],rootStatus[1]);
      }
  
      public int[] dfs(TreeNode root){
         
          if(root == null)return new int[]{
         0,0};
          int[] l = dfs(root.left);
          int[] r = dfs(root.right);
          int rob = root.val + l[1] + r[1];
          int notRob  = Math.max(l[0],l[1]) + Math.max(r[0],r[1]);
          return new int[]{
         rob,notRob};
      }
  

• 分析

  1. 方法一
  2. 这是一道树状dp
  3. 用两个map来存储每个节点的两种状态（偷与不偷）下的最大收益。
  4. 后序遍历到叶子节点，然后逐层向上。
  5. 当前节点不偷的话，那么当前结点的最大值，就等于左右结点的两种状态下的最大收益之和。
  6. 若当前结点偷的话，那么当前结点的最大收益，就等于当前结点的值加上左孩子结点不偷的情况下的最大收益加上右孩子结点不同的情况下的最大收益。
  7. 方法二是对方法一的改进。
  8. 当前节点的最大收益仅于其孩子结点的最大收益有关，所以不需要使用HashMap来记录所有结点的收益。
  9. 仅需要记录其左孩子的两种状态下的最大收益和右孩子的两种状态下的最大收益即可。

• 提交结果

  方法一
  

  方法二
  

338.比特位计数

给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ，计算其二进制数中的 1 的数目并将它们作为数组返回。

进阶:

给出时间复杂度为O(n*sizeof(integer))的解答非常容易。但你可以在线性时间O(n)内用一趟扫描做到吗？
要求算法的空间复杂度为O(n)。
你能进一步完善解法吗？要求在C++或任何其他语言中不使用任何内置函数（如 C++ 中的 __builtin_popcount）来执行此操作。

• 解答

      //方法一   
      public int[] countBits(int num) {
         
          int[] res = new int[num+1];
          for(int i = 0;i<res.length;i++){
         
              res[i] = count(i);
          }
          return res;
      }
      public int count(int x){
         
          int count = 0;
          while(x > 0){
         
              count++;
              x &= x-1;
          }
          return count;
      }
  		//方法二
      public int[] countBits(int num) {
         
          int[] res = new int[num+1];
          res[0] = 0;
          for(int i = 1;i<res.length;i++){
         
              if(i % 2 == 0)
                  res[i] = res[i/2];
              else
                  res[i] = res[i-1] + 1;
          }
          return res;
      }
  

• 分析

  1. 方法一
  2. 当前数字和当前数字减1做与运算，得到新的数字。count++
  3. 若得到新的数字大于0，则继续做第一步的操作。这样就能得到右多少个1。
  4. 方法二
  5. 先观察数字和二进制的规律
  6. 可以发现，偶数的1的个数肯定和这个偶数除以/2的个数一样，因为只是把最低位的1给移除了。
  7. 而奇数比前一位偶数多一个1.
  8. 并且0 的二进制数1个个数是0.所以可以根据以上两条规则去遍历一遍即可。

• 提交结果

  方法一
  

  方法二