POJ 1182 食物链（带权并查集）

POJ 1182 食物链（带权并查集）
前几天在叶某同学的忽悠下，做了这道挺有意思的题目，感觉这道有必要做下记录。刚开始想到大概是绕一个圈子来证明之前的关系是否与当前语句给出关系矛盾，若矛盾，则是假话（就是后来看别人博客的向量的方法，但是我只是有感觉，具体写不出，所以参考了下这位大神的博客：http://hi.baidu.com/tomspirit/item/d1f2a19b2aaf36d27a7f0158）
废话不说，先上题目：
食物链
Time Limit: 1000MS Memory Limit: 10000K
Total Submissions: 48340 Accepted: 14092
Description

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。
现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述：
第一种说法是”1 X Y”，表示X和Y是同类。
第二种说法是”2 X Y”，表示X吃Y。
此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。
1）当前的话与前面的某些真的话冲突，就是假话；
2）当前的话中X或Y比N大，就是假话；
3）当前的话表示X吃X，就是假话。
你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。
Input

第一行是两个整数N和K，以一个空格分隔。
以下K行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中D表示说法的种类。
若D=1，则表示X和Y是同类。
若D=2，则表示X吃Y。
Output

只有一个整数，表示假话的数目。
Sample Input

100 71 101 1 2 1 22 2 3 2 3 3 1 1 3 2 3 1 1 5 5
Sample Output

3
这道题关键判断现在给出的关系和之前所建立的关系是否矛盾，加上数据大，所以采用并查集的方式。之前有一个误区，就是觉得并查集合并的都是同一集合的东西（比如这里说的同类，我做得太少了。。。）。其实不然，并查集不止同类，互相有内在联系的事物也是可以用并查集的，应为并查集其实就是把内在有联系的东西合并为一个集合来提高效率，同类只是一个特殊情况，好比BFS是启发搜索的一个特例。。（自己理解，不一定对）。。

然后 关键点在这里：（所谓的向量方法）可以理解为曲线救国，比如现在有X->Y,Y->B,B->Z 的关系，问Z->X的关系，我们可以通过求X->Y->Y->B->B->Z来得出（Z->X)的关系。跟中学学的向量有点像吧。。。。。
来个图：

大概是这样。。。。（错了还请大神指正）
这里说说一个很关键的前提，是下面的基础：
0 - 这个节点与它的父节点是同类
1 - 这个节点被它的父节点吃
2 - 这个节点吃它的父节点。

struct node
{
int father, relation; //父亲节点和其父亲节点对应的关系
};
然后根据并查集，每个结点都有 各自的父节点（没有的话自己就是自己的父节点），假设按照案例第一个有效的输入2 1 2，（1 101 1，这个是题目中的情况2，无效） ，这里进行一次路径压缩，压缩后因为父节点发生变化，所以其相对父亲节点的关系也要变化

然后第一个维护的关系来了，就是路径压缩，根据并查集的常规做法，在查找过程进行路径压缩，压缩过程就是吧所有子节点的父亲都同一为一个父节点（这个是根）。
int find(int x)
{
if (x == a[x].father)
return x;
int temp=a[x].father;
a[x].father = find(temp);
a[x].relation = (a[x].relation + a[temp].relation)%3;
return a[x].father;
}
int combine(int x, int y,int d)
{
int rootx, rooty;
rootx = find(x);
rooty = find(y);
if (rootx != rooty)
{
a[rooty].father = rootx;
a[rooty].relation = (a[x].relation + d - 1 + 3 - a[y].relation) % 3;
return true;
}
else
{
if (d == 1 && a[x].relation != a[y].relation)
{
sum++; return false;
}
if (d == 2)
{
if ((3 - a[x].relation + a[y].relation)%3 !=d - 1)
sum++;
return false;
}
}
return true;
}
由于根有一个特性就是它的父节点一定是自己，所以我们可以递归处理，先判断是不是跟节点（既是它的父亲是不是它自身），然后不是得话就递归当前节点的父节点。由于递归会走到末尾再逐层回收，所以a[x].father = find(temp);找到的肯定是根节点。自然路径压缩就是吧每一个非父节点的父亲设置为父节点，这样就实现了路径压缩。
这样就会引出一个问题，就是父节点发生变化，则关系也发生变化了。
如上图，a[x].relation是父节点到子节点的关系，所以根据上图，只要顺着向量的思维，由根一直逐层指向儿子，就可以得出根节点和最底层儿子的关系。又因为在这道题中实事上貌似不会超过3层树（错了表怪我，因为FIND函数查找的时候已经路径压缩了），所以我们只需要a[x].relation = (a[x].relation+a[temp].relation)%3（可以穷举下，%3这里我的理解是为了实现向量，用了同余原理，让得出的值在0-2，跟上面约定吻合，这里我感觉理解不透彻，还请大神告诉%3的真正意义，我自己认为是除去那些2+1，因为向量抵消了，就是实现首尾相接首尾连。。。。。）;
然后随着状态压缩后，若是两个不同的集合（根节点不同），我们也需要吧这两个集合合并，就是说，吧一个跟节点合并到宁一个根节点上，然后也是两个根结点之间关系的更新，
（绿色这里是为了求两根节点（RX,RY）之间的关系，所以要反过来得出Y->RY的关系(就是之前是RY相对y的关系，现在是Y相对RY)，这里我参考了别人博客和穷举验证应该是 3 - a[y].relation，然后也是向量原理可以得出RY与RX之间的关系。

所以公式可以得出，RX->X+X->Y+Y->RY=RX->RY（得出的是a[x].relation + d - 1 + 3 - a[y].relation) % 3）一一对应。。
这里若是不在一个集合自然也就不存在矛盾关系了，所以一定是真话，那如果之前已经在同一集合，我们就也是用向量的方法来判断是否与之前的条件矛盾。D-1是当前句子的X和Y的关系，我们根据并查集绕一个圈子，首先就是D=1的情况，也就是说是同类，那么根是一样的，不一样的就不是同类了（。。同一集合），然后他们相对根（父亲）节点的关系也是一样的，不然就是矛盾了。
第二个就是关键，如果d=2，也是曲线救国：如图

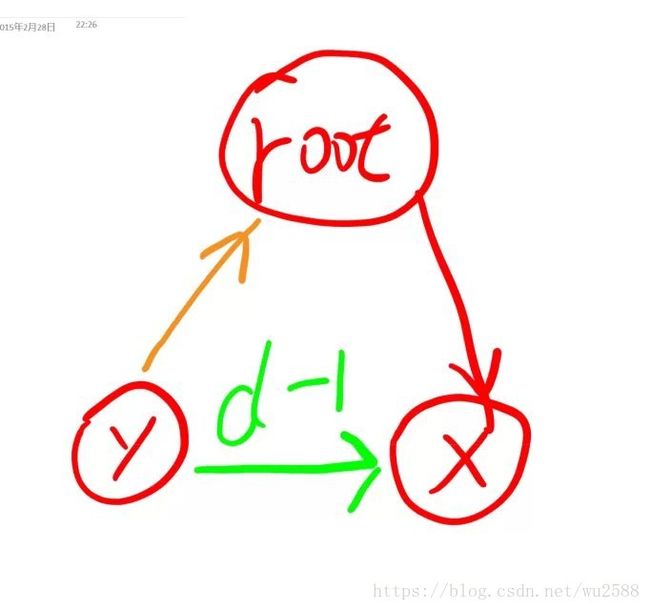
黄色那里跟上面的取反关系一样，也是3 - a[x].relation，如图我们就不难得出以前Y->X的关系是由（3 - a[x].relation + a[y].relation）%3
推出，那自认我们再和数据中的D-1比较是否相等就可以得出真假。
这道题目的主体到这里就结束了，剩下的其他我保留代码文件和测试数据以便以后参考回忆

#include
using namespace std;
int sum;
struct node
{
 int father, relation;
};
node a[50010];
void init()
{
 for (int i = 0; i < 50010; i++)
 {
  a[i].father = i;
  a[i].relation = 0;
 }
 sum = 0;
}
int find(int x)
{

 if (x == a[x].father)
  return x;
 int temp=a[x].father;
 a[x].father =  find(temp);
 a[x].relation = (a[x].relation + a[temp].relation)%3;
 return a[x].father;
}
int combine(int x, int y,int d)
{
 int rootx, rooty;
 rootx = find(x);
 rooty = find(y);
 if (rootx != rooty)
 {
  a[rooty].father = rootx;
  a[rooty].relation = (a[x].relation + d - 1 + 3 - a[y].relation) % 3;
  return true;
 }
 else
 {
  if (d == 1 && a[x].relation != a[y].relation)
  {
   sum++; return false;
  }
  if (d == 2)
  {
   if ((3 - a[x].relation + a[y].relation)%3 !=d - 1)
    sum++;
   return false;
  }
 }
 return true;
}
int main()
{
 int n, k;
 int d, x, y;
 cin >> n >> k;

  init();
  for (int i = 0; i < k; i++)
  {
   scanf("%d%d%d", &d, &x, &y);
   if (x > n || y > n)
   {
    sum++;
    continue;
   }
   if (d == 2 & x == y)
   {
    sum++;
    continue;
   }
   combine(x, y, d);
  }
  cout << sum << endl;

}