神经网络架构搜索——可微分搜索（DAAS）
神经网络架构搜索——可微分搜索（DAAS）
-
-
- 摘要
- 方法
-
- 操作参数 α \alpha α 的离散化损失
- 边参数 β \beta β 的离散化损失
- 基于信息熵的离散化损失
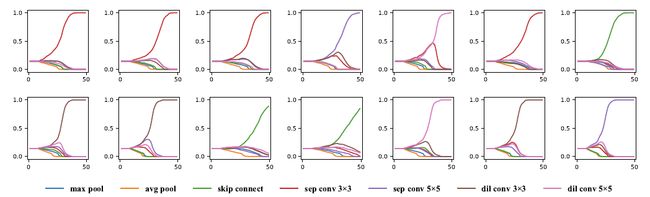
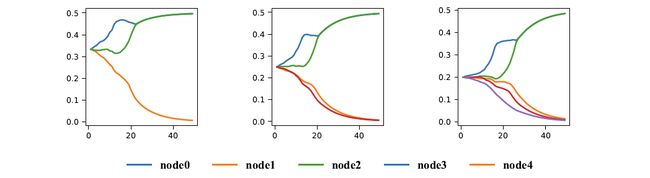
- 损失函数作用的可视化
- 实验结果
-
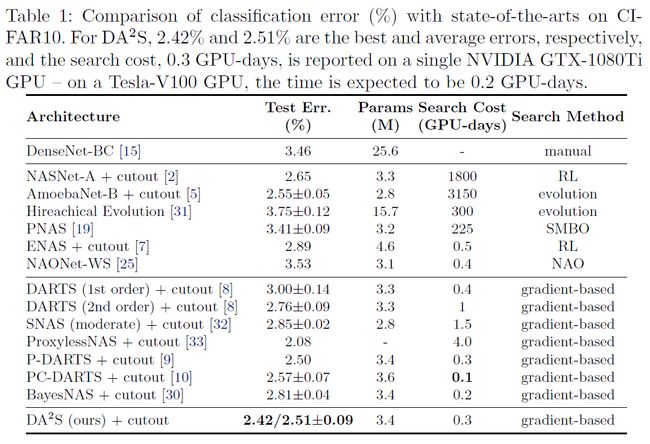
- CIFAR-10
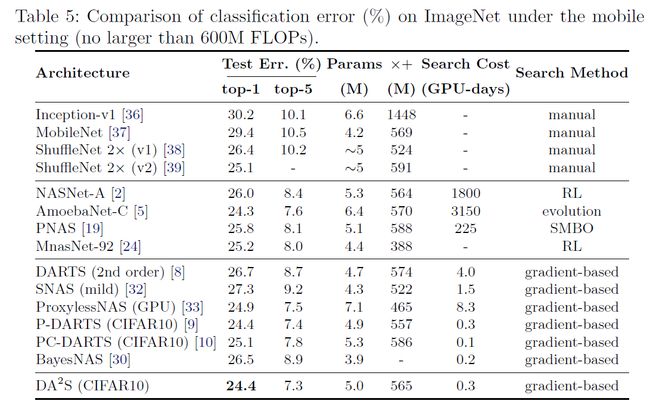
- ImageNet
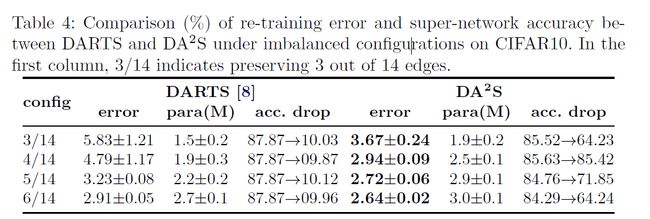
- 消融实验
-
- Error离散化对比
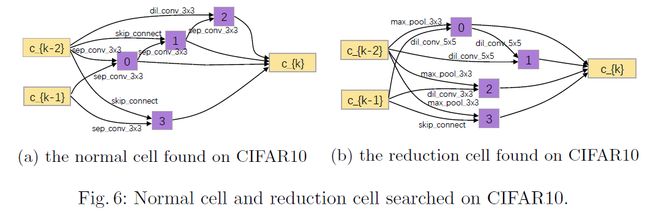
- 操作与边的可视化
-
本文是华为基于可微分网络搜索的论文。本文基于DARTS搜索离散化后性能损失严重的问题，提出了离散化感知架构搜索，通过添加损失项(Discretization Loss)以缓解离散带来的准确性损失。
- 论文题目：Discretization-Aware Architecture Search
- 开源代码： https://github.com/sunsmarterjie/DAAS。
摘要
神经架构搜索（NAS）的搜索成本为通过权值共享方法大大减少。 这些方法通过优化所有可能的边缘和操作的超级网络，从而确定离散化的最佳子网，即修剪弱候选者。在操作或边缘执行离散化过程目前存在的不准确之处以及最终结构的质量不能保证。 本文提出了离散化感知架构搜索（DAAS），其核心思想是添加损失项以推动超级网络朝向所需拓扑的配置，以便离散带来的准确性损失得到缓解。 实验在标准图像分类基准上证明了方法的重要性，尤其是在目标网络不平衡的情况下。
方法
算法的核心思路是采用超网络中边和操作参数归一化后的信息熵作为Loss约束，最小化信息熵可以实现离散的参数分布。
操作参数 α \alpha α 的离散化损失
L i , j O ( α ) = − ∑ o ∈ O exp { α i , j o } ∑ o ′ ∈ O exp { α i , j o ′ } ⋅ log exp { α i , j o } ∑ o ′ ∈ O exp { α i , j o ′ } \mathcal{L}_{i, j}^{\mathrm{O}}(\boldsymbol{\alpha})=-\sum_{o \in \mathcal{O}} \frac{\exp \left\{\alpha_{i, j}^{o}\right\}}{\sum_{\boldsymbol{o}^{\prime} \in \mathcal{O}} \exp \left\{\alpha_{i, j}^{o^{\prime}}\right\}} \cdot \log \frac{\exp \left\{\alpha_{i, j}^{o}\right\}}{\sum_{o^{\prime} \in \mathcal{O}} \exp \left\{\alpha_{i, j}^{o^{\prime}}\right\}} Li,jO(α)=−o∈O∑∑o′∈Oexp{ αi,jo′}exp{ αi,jo}⋅log∑o′∈Oexp{ αi,jo′}exp{ αi,jo}
L O ( α ) = ∑ j ∑ i < j L i , j O ( α ) \mathcal{L}^{\mathrm{O}}(\boldsymbol{\alpha})=\sum_{j} \sum_{i < j} \mathcal{L}_{i, j}^{\mathrm{O}}(\boldsymbol{\alpha}) LO(α)=j∑i<j∑Li,jO(α)
边参数 β \beta β 的离散化损失
L j E ( β ) = − ∑ i < j exp { β i , j } ∑ i ′ < j exp { β i ′ , j } ⋅ log exp { β i , j } ∑ i ′ < j exp { β i ′ , j } + ∣ ∑ B β i , j − 2 ∣ 2 \mathcal{L}_{j}^{\mathrm{E}}(\boldsymbol{\beta})=-\sum_{i < j} \frac{\exp \left\{\beta_{i, j}\right\}}{\sum_{i^{\prime} < j} \exp \left\{\beta_{i^{\prime}, j}\right\}} \cdot \log \frac{\exp \left\{\beta_{i, j}\right\}}{\sum_{i^{\prime} < j} \exp \left\{\beta_{i^{\prime}, j}\right\}}+\left|\sum_{B} \beta_{i, j}-2\right|^{2} LjE(β)=−i<j∑∑i′<jexp{ βi′,j}exp{ βi,j}⋅log∑i′<jexp{ βi′,j}exp{ βi,j}+∣∣∣∣∣B∑βi,j−2∣∣∣∣∣2
L E ( β ) = ∑ j L j E ( β ) \mathcal{L}^{\mathrm{E}}(\boldsymbol{\beta})=\sum_{j} \mathcal{L}_{j}^{\mathrm{E}}(\boldsymbol{\beta}) LE(β)=j∑LjE(β)
∣ ∑ B β i , j − 2 ∣ 2 \left|\sum_{B} \beta_{i, j}-2\right|^{2} ∣∑Bβi,j−2∣2，该项的主要目的是为了维持保留边的均匀性，因为，每个节点保留两条边，因此设置为2。以5条边为例，与前面信息熵对应，最佳的 β \beta β取值为两个保留边的取值均为1，其他边的取值为0。
基于信息熵的离散化损失
L ( θ , α , β ) = L C ( α , θ ) + L O ( α ) + L E ( β ) \mathcal{L}(\boldsymbol{\theta}, \boldsymbol{\alpha}, \boldsymbol{\beta})=\mathcal{L}^{\mathrm{C}}(\boldsymbol{\alpha}, \boldsymbol{\theta})+\mathcal{L}^{\mathrm{O}}(\boldsymbol{\alpha})+\mathcal{L}^{\mathrm{E}}(\boldsymbol{\beta}) L(θ,α,β)=LC(α,θ)+LO(α)+LE(β)
L ( θ , α , β ) = L C ( α , θ ) + λ c ( λ α L O ( α ) + λ β L E ( β ) ) \mathcal{L}(\boldsymbol{\theta}, \boldsymbol{\alpha}, \boldsymbol{\beta})=\mathcal{L}^{\mathrm{C}}(\boldsymbol{\alpha}, \boldsymbol{\theta})+\lambda_{c}\left(\lambda_{\boldsymbol{\alpha}} \mathcal{L}^{\mathrm{O}}(\boldsymbol{\alpha})+\lambda_{\boldsymbol{\beta}} \mathcal{L}^{\mathrm{E}}(\boldsymbol{\beta})\right) L(θ,α,β)=LC(α,θ)+λc(λαLO(α)+λβLE(β))
最终完整的Loss分布，各个Loss受到超参的约束。在这里，文章对超参的渐进式设置做了不同的探索。渐进式超参对前期Weights的充分训练和后期架构参数的离散化分布起到了关键作用！
损失函数作用的可视化
实验结果
CIFAR-10
ImageNet
消融实验
Error离散化对比
操作与边的可视化
