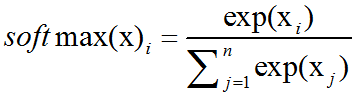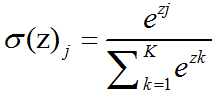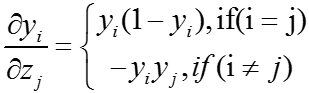激活函数之softmax介绍及C++实现
下溢(underflow):当接近零的数被四舍五入为零时发生下溢。许多函数在其参数为零而不是一个很小的正数时才会表现出质的不同。例如,我们通常要避免被零除或避免取零的对数。
上溢(overflow):当大量级的数被近似为∞或-∞时发生上溢。进一步的运算通常会导致这些无限值变为非数字。
必须对上溢和下溢进行数值稳定的一个例子是softmax函数(softmax function).softmax函数经常用于预测与Multinoulli分布相关联的概率,定义为:
考虑一下当所有xi都等于某个常数c时会发生什么。从理论分析上说,我们可以发现所有的输出都应该为1/n。从数值计算上说,当c量级很大时,这可能不会发生。如果c是很小的负数,exp(c)就会下溢。这意味着softmax函数的分母会变成0,所以最后的结果是未定义的。当c是非常大的正数时,exp(c)的上溢再次导致整个表达式未定义。这两个困难能通过计算softmax(z)同时解决,其中z=x-maxixi.简单的代数计算表明,softmax解析上的函数值不会因为从输入向量减去或加上标量而改变。减去maxixi导致exp的最大参数为0,这排除了上溢的可能性。同样地,分母中至少有一个值为1的项,这就排除了因分母下溢而导致被零除的可能性。
还有一个小问题。分子中的下溢仍可以导致整体表达式被计算为零。这意味着,如果我们在计算log(softmax(x))时,先计算softmax再把结果传给log函数,会错误地得到-∞。相反,我们必须实现一个单独的函数,并以数值稳定的方式计算log(softmax)。我们可以使用相同的技巧来稳定log(softmax)函数。
Softmax函数:在数学,尤其是概率论和相关领域中,Softmax函数,或称归一化指数函数,是逻辑函数的一种推广。它能将一个含任意实数的K维的向量z的”压缩”到另一个K维实向量σ(z)中,使得每一个元素的范围都在(0,1)之间,并且所有元素的和为1。该函数的形式通常按下面的式子给出:其中,j=1,…,K.
Softmax函数实际上是有限项离散概率分布的梯度对数归一化。因此,Softmax函数在包括多项逻辑回归,多项线性判别分析,朴素贝叶斯分类器和人工神经网络等的多种基于概率的多分类问题方法中都有着广泛应用。
The softmax function is often used in the final layer of a neural network-based classifier. Such networks are commonly trained under a log loss (or cross-entropy) regime, giving a non-linear variant of multinomial logistic regression.
Softmax可作为神经网络中的输出层,用于多分类(sigmoid只能用于二分类,而softmax可用于多分类。使用Logistic函数来实现二分类问题,对于多分类问题,可以使用多项Logistic回归,该方法也被称之为softmax函数);Softmax还可以解决学习速度衰退的问题;softmax还可作为loss function。
softmax函数的导数如下:
以上内容主要摘自:《深度学习中文版》 和 维基百科
以下是C++实现的测试code:
#include "funset.hpp"
#include
#include
#include
#include
#include
#include "common.hpp"
// ========================= Activation Function: softmax =====================
template
int activation_function_softmax(const _Tp* src, _Tp* dst, int length)
{
const _Tp alpha = *std::max_element(src, src + length);
_Tp denominator{ 0 };
for (int i = 0; i < length; ++i) {
dst[i] = std::exp(src[i] - alpha);
denominator += dst[i];
}
for (int i = 0; i < length; ++i) {
dst[i] /= denominator;
}
return 0;
}
template
int activation_function_softmax_derivative(const _Tp* src, _Tp* dst, int length)
{
std::vector<_Tp> y(length, (_Tp)0);
activation_function_softmax(src, y.data(), length);
fprintf(stderr, "Error: activation_function_softmax_derivative to do ...\n");
return -1;
}
int test_activation_function()
{
std::vector src{ 1.23f, 4.14f, -3.23f, -1.23f, 5.21f, 0.234f, -0.78f, 6.23f };
int length = src.size();
std::vector dst(length);
fprintf(stderr, "source vector: \n");
fbc::print_matrix(src);
fprintf(stderr, "calculate activation function:\n");
fprintf(stderr, "type: sigmoid result: \n");
fbc::activation_function_sigmoid(src.data(), dst.data(), length);
fbc::print_matrix(dst);
fprintf(stderr, "type: sigmoid derivative result: \n");
fbc::activation_function_sigmoid_derivative(src.data(), dst.data(), length);
fbc::print_matrix(dst);
fprintf(stderr, "type: sigmoid fast result: \n");
fbc::activation_function_sigmoid_fast(src.data(), dst.data(), length);
fbc::print_matrix(dst);
fprintf(stderr, "type: softplus result: \n");
fbc::activation_function_softplus(src.data(), dst.data(), length);
fbc::print_matrix(dst);
fprintf(stderr, "type: softplus derivative result: \n");
fbc::activation_function_softplus_derivative(src.data(), dst.data(), length);
fbc::print_matrix(dst);
fprintf(stderr, "type: ReLU result: \n");
fbc::activation_function_ReLU(src.data(), dst.data(), length);
fbc::print_matrix(dst);
fprintf(stderr, "type: ReLU derivative result: \n");
fbc::activation_function_ReLU_derivative(src.data(), dst.data(), length);
fbc::print_matrix(dst);
fprintf(stderr, "type: Leaky ReLUs result: \n");
fbc::activation_function_Leaky_ReLUs(src.data(), dst.data(), length);
fbc::print_matrix(dst);
fprintf(stderr, "type: Leaky ReLUs derivative result: \n");
fbc::activation_function_Leaky_ReLUs_derivative(src.data(), dst.data(), length);
fbc::print_matrix(dst);
fprintf(stderr, "type: Leaky ELUs result: \n");
fbc::activation_function_ELUs(src.data(), dst.data(), length);
fbc::print_matrix(dst);
fprintf(stderr, "type: softmax result: \n");
fbc::activation_function_softmax(src.data(), dst.data(), length);
fbc::print_matrix(dst);
fprintf(stderr, "type: softmax derivative result: \n");
fbc::activation_function_softmax_derivative(src.data(), dst.data(), length);
fbc::print_matrix(dst);
return 0;
} GitHub: https://github.com/fengbingchun/NN_Test