《数学建模算法与应用第二版》——chapter12. 现代优化算法

1. 模拟退火算法

1.1 算法简介

1.2 应用举例

clc, clear
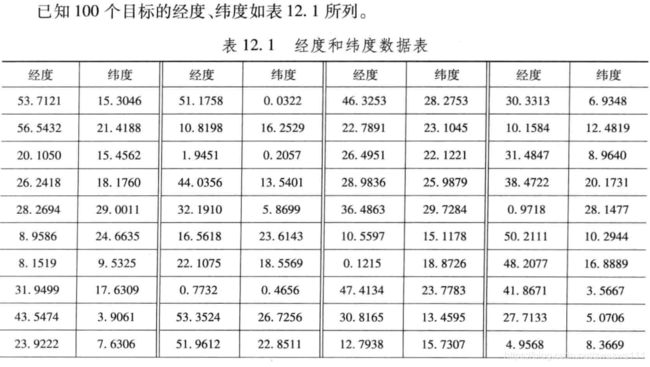
sj0=load('sj.txt');    %加载100个目标的数据，数据按照表格中的位置保存在纯文本文件sj.txt中
x=sj0(:,[1:2:8]);x=x(:);
y=sj0(:,[2:2:8]);y=y(:);
sj=[x y]; d1=[70,40]; 
sj=[d1;sj;d1]; sj=sj*pi/180; %角度化成弧度
d=zeros(102); %距离矩阵d初始化
for i=1:101
   for j=i+1:102
d(i,j)=6370*acos(cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)));
   end
end
d=d+d';
path=[];long=inf; %巡航路径及长度初始化
rand('state',sum(clock));  %初始化随机数发生器
for j=1:1000  %求较好的初始解
    path0=[1 1+randperm(100),102]; temp=0;
    for i=1:101
        temp=temp+d(path0(i),path0(i+1));
    end
    if temprand
  path=[path(1:c1-1),path(c2:-1:c1),path(c2+1:102)]; long=long+df;
  end
  T=T*at;
   if T

计算结果为44h左右。

2. 遗传算法

2.1 算法简介

2.2 模型及算法

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%如有格式问题请使用matlab自动对齐功能%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc,clear
sj0=load('sj.txt');       %加载100个目标的数据
x=sj0(:,1:2:8); x=x(:);
y=sj0(:,2:2:8); y=y(:);
sj=[x y]; d1=[70,40]; 
sj=[d1;sj;d1]; sj=sj*pi/180;  %单位化成弧度
d=zeros(102); %距离矩阵d的初始值
for i=1:101
  for j=i+1:102
  d(i,j)=6370*acos(cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)));
  end
end
d=d+d'; w=50; g=100; %w为种群的个数，g为进化的代数
rand('state',sum(clock)); %初始化随机数发生器
for k=1:w  %通过改良圈算法选取初始种群
    c=randperm(100); %产生1，...，100的一个全排列  
    c1=[1,c+1,102]; %生成初始解
    for t=1:102 %该层循环是修改圈 
        flag=0; %修改圈退出标志
    for m=1:100
      for n=m+2:101
        if d(c1(m),c1(n))+d(c1(m+1),c1(n+1))

3. 改进的遗传算法

3.1 引言

无人机航路规划问题实际上是一个组合优化问题，是优化理论中的NP-hard问题。因为其解空间不连续，解邻域表达困难，所以难以用通常的算法求解。遗传算法作为现代优化算法之一，其主要特点是对非线性极值问题能以概率1跳出局部最优解，找到全局最优解。而遗传算法这种跳出局部最优寻找全局最优特性都基于算法中的交叉和变异。在传统遗传算法的结构中，变异操作在交叉操作基础上进行，强调的是交叉作用，认为变异只是一个生物学背景机制。在具体交叉操作中，人们通常采用单点交叉（段交叉）、多点交叉与均匀交叉，其中单点交叉是指随机地在基因序列中选择一个断点，然后交换双亲上断点右端的所有染色体。在变异操作中，变异算子一般是用Guassian 分布的随机变异来实现。近年来，也有学者尝试用Cauchy分布的随机序列来实现变异，希望通过Cauchy 分布宽大的两翼特性实现更大范围的变异，以利于找到全局最优解。Rudolph 从理论上分析了采用Cauchy 分布随机变异进化算法的局部收敛性。Chelapilla进一步把二者结合起来，采用两种分布的线性叠加，但仿真结果显示，算法改进效果并不十分明显。将生物进化看成是随机性加上反馈，并指出其中的随机性主要是由系统的内在因素所引起，而不是由外部环境的随机扰动所造成。而混沌系统在其混沌域中表现为随机性，它是确定系统内部随机性的反映，不同于外在的随机特性。本节根据以上特点对基于求解航路规划的遗传算法进行改进，首先将变异操作从交叉操作中分离出来，使其成为独立的并列于交叉的寻优操作，在具体遗传操作中，混沌与遗传操作联系在一起，在交叉操作中，以"门当户对"原则进行个体的配对，利用混沌序列确定交叉点，实行强度最弱的单点交叉，以确保算法收敛精度，削弱和避免寻优抖振问题;在变异操作中，利用混沌序列对染色体中多个基因进行变异，以避免算法早熟。

3.2 模型及算法

4. matlab遗传算法工具箱

4.1 遗传算法与搜索工具箱概述

4.2 使用遗传算法工具箱初步

4.3 直接搜索工具

原课本习题及代码

点击下载 【课本 + 源码 】 提取码：92h8