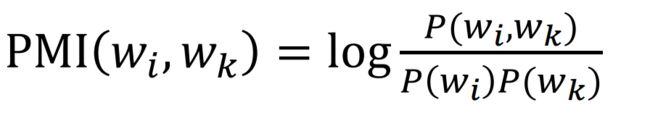Word2vec

分词与词向量

今天/天气/不错/!(结巴分词)

1.启发式:Heuristic

2.机器学习/统计方法:HMM, CRF

基本假设：“相似”词的邻居词分布类似

倒推：两个词邻居词分布类似 → 两个词语义相近

猫 宠物 主人 喂食 蹭 喵

狗 宠物 主人 喂食 咬 汪

v(“猫”)≈v(“狗”)

v(“喵”)≈v(“汪”)

词向量:

1.传统one-hot编码 ( “天气”: (1,0,0…,0)， “气候”: (0,1,0,…0) )

维度高（几千–几万维稀疏向量），数据稀疏

难以计算词之间相似度

难以做模糊匹配

2.词嵌入

维度低（ 100 – 500维）

无监督学习，不需去掉停用词(stopwords)

天然有聚类后的效果

连续向量，方便机器学习模型处理

罕见词： “风姿绰约” ≈ “漂亮”

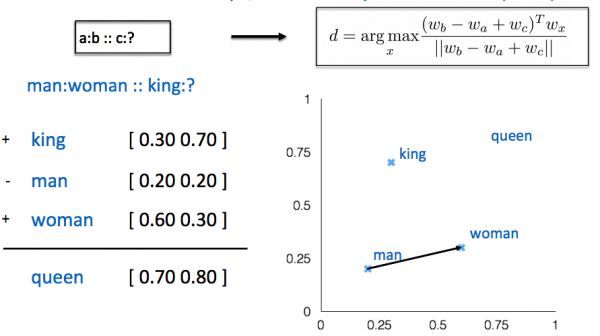
上图中通过man和woman的向量,可以求cos相似度得出与king最接近的向量是queen.

Word2vec

Huffman树(最优二叉树):

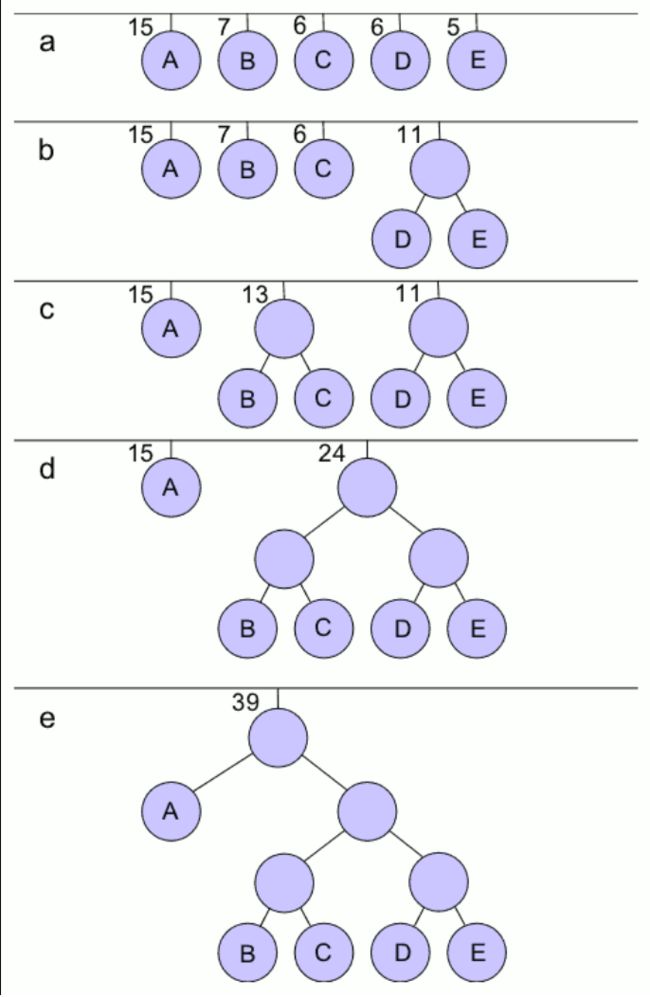
Huffman树是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。

构建huffman树:

输入

符号集合 S = { s 1 , s 2 , ⋯ , s n }，其S集合的大小为 n。

权重集合 W = { w 1 , w 2 , ⋯ , w n } ，其W集合不为负数且 wi = weight(si), 1 ≤ i ≤ n。

输出

一组编码 C(S,W)={c1,c2, ⋯ ,cn} ，其C集合是一组二进制编码且ci为si相对应的编码， 1 ≤ i ≤ n。

目标

设 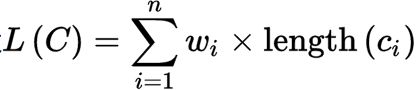为C的加权的路径长，对所有编码 T(S,W)，则L(C) ≤ L(T)

例如:

 

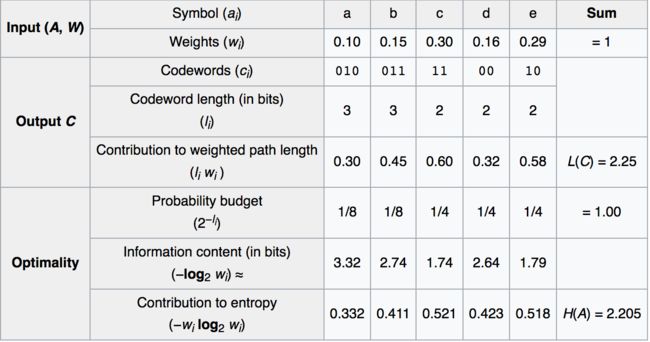
Huffman编码:

Huffman编码使用变长编码表对源符号（如文件中的一个字母）进行编码，其中变长编码表是通过一种评估来源符号出现概率的方法得到的，出现概率高的字母使用较短的编码，反之出现概率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

构建Huffman编码是一个通过哈夫曼树进行的一种编码，一般情况下，以字符：‘0’与‘1’表示。编码的实现过程很简单，只要实现哈夫曼树，通过遍历哈夫曼树，规定向左子树遍历一个节点编码为“0”，向右遍历一个节点编码为“1”，结束条件就是遍历到叶子节点！

例如:

n-gram模型:

n-gram模型是基于(n-1)阶马尔可夫链的一种概率语言模型，该模型基于这样一种假设，第n个词的出现只与前面N-1个词相关，而与其它任何词都不相关，整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。当n分别为1、2、3时，又分别称为一元语法（unigram）、二元语法（bigram）与三元语法（trigram）

推导:

假设T是由词序列W1,W2,W3,…Wn组成的，那么P(T)=P(W1W2W3...Wn)=P(W1)P(W2|W1)P(W3|W1W2)…P(Wn|W1W2…Wn-1)

但是这种方法存在两个致命的缺陷：一个缺陷是参数空间过大，不可能实用化；另外一个缺陷是数据稀疏严重。

为了解决这个问题，我们引入了马尔科夫假设：一个词的出现仅仅依赖于它前面出现的有限的一个或者几个词。

如果一个词的出现仅依赖于它前面出现的一个词，那么我们就称之为bigram。即

P(T) = P(W1W2W3…Wn)=P(W1)P(W2|W1)P(W3|W1W2)…P(Wn|W1W2…Wn-1)

　　 ≈P(W1)P(W2|W1)P(W3|W2)…P(Wn|Wn-1)

如果一个词的出现仅依赖于它前面出现的两个词，那么我们就称之为trigram。

依赖词的个数“n”的选择:

理论上，只要有足够大的语料， n越大越好

实际情况往往是训练语料很有限，很容易产生数据稀疏，不满足大数定律，算出来的概率失真。

另一方面，如果n很大， 参数空间过大，产生维数灾难，也无法实用。

trigram用的最多。尽管如此，原则上，能用bigram解决，绝不使用trigram。 n取≥4的情况较少

当ｎ更大时：对下一个词出现的约束信息更多，具有更大的辨别力；

当ｎ更小时：在训练语料库中出现的次数更多，具有更可靠的统计信息，具有更高的可靠性、实用性。

Word2vec为一群用来产生word embeding(词嵌入)的模型。这些模型为浅层和双层神经网络，训练完成之后，word2vec 模型可用来映射每个词到一个向量，可用来表示词对词之间的关系。该向量为神经网络之隐藏层.Word2vec 依赖skip-grams 或continuous-bag-of-words（CBOW）来建立神经词嵌入。

基本思想:

通过训练将每个词映射成 K 维实数向量（K 一般为模型中的超参数），通过词之间的距离（比如 cosine 相似度、欧氏距离等）来判断它们之间的语义相似度.其采用一个 三层的神经网络 ，输入层-隐层-输出层。有个核心的技术是 根据词频用Huffman编码 ，使得所有词频相似的词隐藏层激活的内容基本一致，出现频率越高的词语，他们激活的隐藏层数目越少，这样有效的降低了计算的复杂度，结果是将相似的词距离越拉越近， 非相似的词越拉越远。

两套模型:

Skip-gram和CBOW

两套减少训练时间框架:

Hierarchical Softmax和Negative Sampling

 

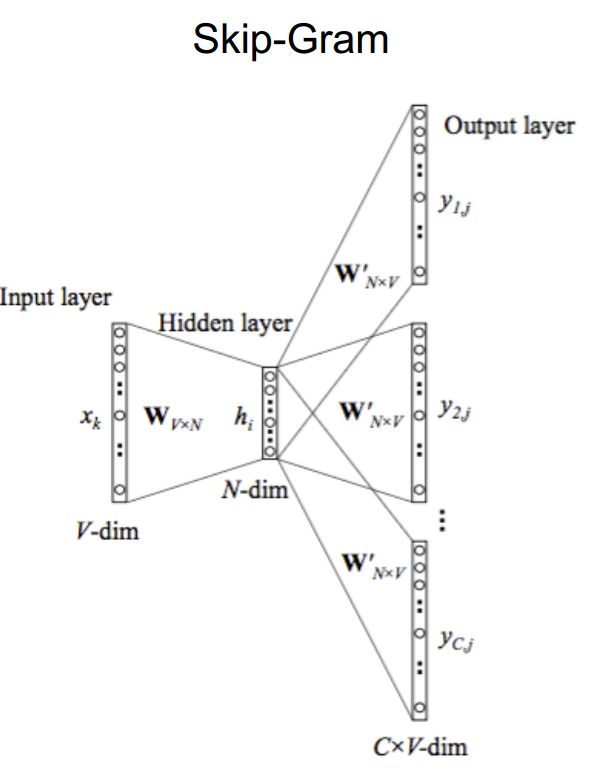
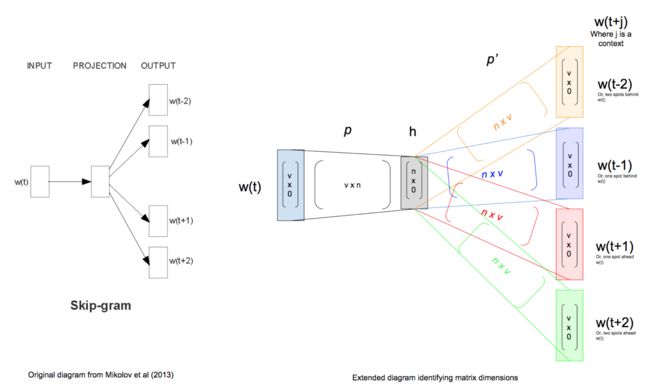
Skip-gram(已知当前词$w_t$,预测上下文$w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m}$):

1.输入层， one hot表示，当前词是1，其他是0  

2.输入层到隐层的连接矩阵，即前面说的W

3.隐层的激活函数很特殊，是f(x) =x. 所以隐层的输出值其实就是当前词的表示Wi

4.隐层到输出层的链接矩阵，即前面说的C

5.输出层是个softmax

 

上图是用于训练示例的Skip-gram网络的扩展描述，向前馈给表示上下文窗口c = 2的输出上下文向量。输入字是词汇大小的单热编码向量。这连接到由我们的节点大小参数定义为大小len（n）的投影层。通过线性变换通过输入权重矩阵p（v x n维）投影输入层。在上下文大小为2的情况下，每个训练样例将向前馈4次4个输出向量：w（t-2），w（t-1），w（t + 1）和w（t + 2）。投影层通过具有n×v维度的输出权重矩阵p'连接到输出层。

从左到右，每个后续层都是通过数学方法构造一个层的点积及其权重矩阵。

权重矩阵p和p'可以以许多方式初始化，最终将使用反向传播进行调整。

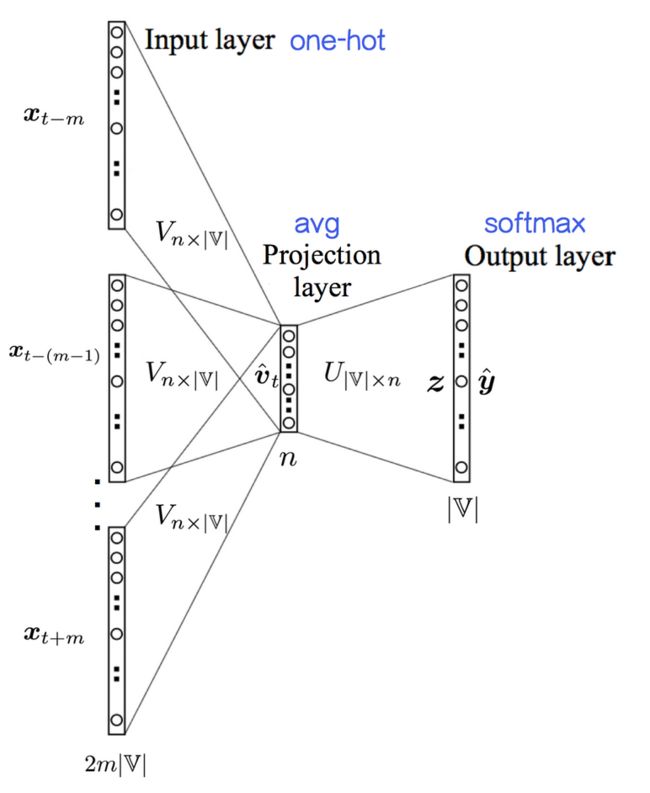
CBOW(已知上下文$w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m}$,预测当前词$w_t$):

输入层：2m×|?|个节点，上下文共 2m个词的one-hot 编码

　　输入层到投影层到连接边：输入词矩阵 Vn×|?|；

投影层：：n个节点，上下文共 2m个词的词向量的平均值；

　　投影层到输出层的连接边：输出词矩阵 U|?|×n；

输出层：|?|个节点。第 i 个节点代表中心词是词 wi的概率。

　　将one-hot到word embedding那一步描述了出来。这里的投影层并没有做任何的非线性激活操作，直接就是Softmax层。

 

 

 

 

 

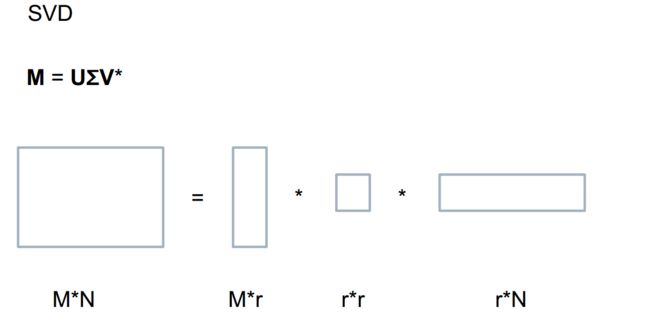
  Word2vec 和矩阵分解的等价性

1.Word2vec 理论上等价于分解 Pointwise Mutual Information (PMI) 矩阵

 

word2vec

 

转载于:https://www.cnblogs.com/xmeo/p/6474833.html