PCL：利用霍夫变换进行直线检测

最近涉及到直线检测的东西，所以查了查资料，发现大多数都是图像方面的，没查到点云方面的资料，给出的源码很多也是利用opencv完成，有点心累，所以还是自己写一下霍夫变换吧。
具体原理，看大神解释（直线检测，圆检测等----）：https://blog.csdn.net/shanchuan2012/article/details/74010561
需求：在XOY平面内，检测混有噪声的点云数据中的直线。
实现步骤：

1. 数据量大的情况，可以进行一下体素化的下采样，不改变整体的点云分布。
2. 将点云在二维平面内画规则格网，横轴为角度，纵轴为长度，设定步长，我取了横轴1度一个步长，纵轴0.5米，将点云从y=kx+b空间按照下面的公式转换到霍夫空间。
   
   截距式的直线方程，往往会交于一点，为了避免斜率无穷大的情况，用了极坐标表示直线，道理雷同，会交于一点。
   
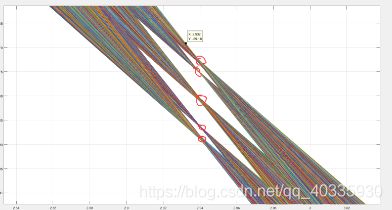
3. 接下来就是求交点的过程，因为通常情况下，点为离散点，不可能完全交于一个点，所以，需要求局部极值大点。（下图霍夫空间中有五个极值点，说明有五条直线，如何将五个节点求出来是个问题）。
   
   我求极值点的方法：
   求解每个点、每个角度步长对应的长度值，算一下它分属于哪一个格网，将所有点进行计算，对格网内数值进行累加（到最后平均数即为该交点的长度值，即rho值），对每个格网进行计数，如果存在格网内点数量比邻域8格网内的点数量都多，我们认为他是极值点。
   但是，会发现其实极值点的数还是挺多的，远不止五个，所以还需要加入另一个阈值，格网内的最小点数，大于它才能判断为极值点。
   所以，这个参数其实挺难确定的，如果事先知道有几条直线，就省事了—所以，选择了两种方式进行计算（1.指定格网最小数量阈值，2，指定格网最小数量阈值和直线个数阈值），看到底符合哪个需求了-----

上代码，vs2013+pcl1.8.0

（运行效率低的话，可以试试release模式下跑）：
可以提供一下示例数据：https://pan.baidu.com/s/1HWIHyxEVENzuCG0_OyzX0A

//HOUGH_LINE.h文件
#pragma once
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace pcl;
using namespace Eigen;
using namespace std;
typedef PointXYZ PointT;
class HOUGH_LINE
{
public:
	HOUGH_LINE();
	~HOUGH_LINE();
	template void vector_sort(std::vector vector_input, std::vector &idx);
	inline void setinputpoint(PointCloud::Ptr point_);
	void VoxelGrid_(float size_, PointCloud::Ptr &voxel_cloud);
	void draw_hough_spacing();
	void HOUGH_line(int x_setp_num, double y_resolution, int grid_point_number_threshold, vector&K_, vector&B_, int line_num=-1);
	void draw_hough_line();
private:
	PointCloud::Ptr cloud;
	int point_num;
	PointT point_min;
	PointT point_max;
	vector>result_;
};

templatevoid
HOUGH_LINE::vector_sort(std::vector vector_input, std::vector &idx){
	idx.resize(vector_input.size());
	iota(idx.begin(), idx.end(), 0);
	sort(idx.begin(), idx.end(), [&vector_input](size_t i1, size_t i2) { return vector_input[i1] > vector_input[i2]; });
}
inline void HOUGH_LINE::setinputpoint(PointCloud::Ptr point_){
	cloud = point_;
	point_num = cloud->size();
}

//HOUGH_LINE.cpp文件
#include "HOUGH_LINE.h"
HOUGH_LINE::HOUGH_LINE()
{
}

HOUGH_LINE::~HOUGH_LINE()
{
	cloud->clear();
	result_.clear();
}
void HOUGH_LINE::VoxelGrid_(float size_,PointCloud::Ptr &voxel_cloud){
	PointCloud::Ptr tem_voxel_cloud(new PointCloud);
	VoxelGrid vox;
	vox.setInputCloud(cloud);
	vox.setLeafSize(size_, size_, size_);
	vox.filter(*tem_voxel_cloud);
	cloud = tem_voxel_cloud;
	voxel_cloud = tem_voxel_cloud;
	point_num = cloud->size();
}
void HOUGH_LINE::draw_hough_spacing(){
	visualization::PCLPlotter *plot_(new visualization::PCLPlotter("Elevation and Point Number Breakdown Map"));
	plot_->setBackgroundColor(1, 1, 1);
	plot_->setTitle("hough space");
	plot_->setXTitle("angle");
	plot_->setYTitle("rho");
	vector>data_;
	double x_resolution1 = M_PI / 181;
	double a_1, b_1;
	for (int i_point = 0; i_point < point_num; i_point++)
	{
		a_1 = cloud->points[i_point].x;
		b_1 = cloud->points[i_point].y;
		for (int i = 0; i < 181; i++)
		{
			data_.push_back(make_pair(i*x_resolution1, a_1 * cos(i*x_resolution1) + b_1 * sin(i*x_resolution1)));
		}
		plot_->addPlotData(data_,"line",vtkChart::LINE);//X,Y均为double型的向量
		data_.clear();
	}
	plot_->setShowLegend(false);
	plot_->plot();//绘制曲线
}
void HOUGH_LINE::HOUGH_line(int x_setp_num, double y_resolution, int grid_point_number_threshold, vector&K_, vector&B_,int line_num){
	vector>all_point_row_col;
	vector Grid_Index;
	getMinMax3D(*cloud, point_min, point_max);
	double x_resolution = M_PI / x_setp_num;
	int raster_rows, raster_cols;
	raster_rows = ceil((M_PI - 0) / x_resolution);
	raster_cols = ceil((point_max.y + point_max.x) / y_resolution) * 2;
	MatrixXi all_row_col(raster_cols, raster_rows);//存储每个格网内的个数
	all_row_col.setZero();
	MatrixXd all_row_col_mean(raster_cols, raster_rows);//存储每个格网内的均值
	//统计每个格网内的数量，和rho均值
	all_row_col_mean.setZero();
	double a_, b_;
	for (int i_point = 0; i_point < point_num; i_point++){
		a_ = cloud->points[i_point].x;
		b_ = cloud->points[i_point].y;
		for (int i_ = 0; i_ < x_setp_num; i_++)
		{
			double theta = 0 + i_*x_resolution + x_resolution / 2;
			double rho = a_ * cos(theta) + b_ * sin(theta);
			//double rho = line_(theta,a_,b_);
			double idx = ceil(abs(rho / y_resolution));
			if (rho >= 0)
			{
				all_row_col(raster_cols / 2 - idx, i_) += 1;
				all_row_col_mean(raster_cols / 2 - idx, i_) += rho;
			}
			else{
				all_row_col(raster_cols / 2 + idx, i_) += 1;
				all_row_col_mean(raster_cols / 2 + idx, i_) += rho;
			}
		}
	}
	//求解邻域
	int min_num_threshold = grid_point_number_threshold;
	vector>result_jz;
	//vector>result_;
	vectortem_nebor;
	vectornum_grid;
	for (int i_row = 0; i_row < all_row_col.rows(); i_row++)
	{
		for (int i_col = 0; i_col < all_row_col.cols(); i_col++)
		{
			if (i_row == 0)
			{
				if (i_col == 0)
				{
					tem_nebor.push_back(all_row_col(i_row, i_col + 1));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col + 1));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col));
				}
				if (i_col == all_row_col.cols() - 1)
				{
					tem_nebor.push_back(all_row_col(i_row, i_col - 1));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col - 1));
				}
				if (i_col != all_row_col.cols() - 1 && i_col != 0)
				{
					tem_nebor.push_back(all_row_col(i_row, i_col - 1));
					tem_nebor.push_back(all_row_col(i_row, i_col + 1));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col - 1));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col + 1));
				}
			}
			if (i_row == all_row_col.rows() - 1)
			{
				if (i_col == 0)
				{
					tem_nebor.push_back(all_row_col(i_row - 1, i_col));
					tem_nebor.push_back(all_row_col(i_row - 1, i_col + 1));
					tem_nebor.push_back(all_row_col(i_row, i_col + 1));
				}
				if (i_col == all_row_col.cols() - 1)
				{
					tem_nebor.push_back(all_row_col(i_row - 1, i_col));
					tem_nebor.push_back(all_row_col(i_row - 1, i_col - 1));
					tem_nebor.push_back(all_row_col(i_row, i_col - 1));
				}
				if (i_col != all_row_col.cols() - 1 && i_col != 0)
				{
					tem_nebor.push_back(all_row_col(i_row, i_col - 1));
					tem_nebor.push_back(all_row_col(i_row, i_col + 1));
					tem_nebor.push_back(all_row_col(i_row - 1, i_col));
					tem_nebor.push_back(all_row_col(i_row - 1, i_col - 1));
					tem_nebor.push_back(all_row_col(i_row - 1, i_col + 1));
				}
			}
			if (i_row != all_row_col.rows() - 1 && i_row != 0)
			{
				if (i_col == 0)
				{
					tem_nebor.push_back(all_row_col(i_row, i_col + 1));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col + 1));
					tem_nebor.push_back(all_row_col(i_row - 1, i_col));
					tem_nebor.push_back(all_row_col(i_row - 1, i_col + 1));
				}
				if (i_col == all_row_col.cols() - 1)
				{
					tem_nebor.push_back(all_row_col(i_row - 1, i_col));
					tem_nebor.push_back(all_row_col(i_row - 1, i_col - 1));
					tem_nebor.push_back(all_row_col(i_row, i_col - 1));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col - 1));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col));
				}
				if (i_col != all_row_col.cols() - 1 && i_col != 0)
				{
					tem_nebor.push_back(all_row_col(i_row, i_col - 1));
					tem_nebor.push_back(all_row_col(i_row, i_col + 1));
					tem_nebor.push_back(all_row_col(i_row - 1, i_col));
					tem_nebor.push_back(all_row_col(i_row - 1, i_col - 1));
					tem_nebor.push_back(all_row_col(i_row - 1, i_col + 1));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col - 1));
					tem_nebor.push_back(all_row_col(i_row + 1, i_col + 1));
				}
			}
			int max_tem = *max_element(tem_nebor.begin(), tem_nebor.end());
			tem_nebor.clear();
			if (all_row_col(i_row, i_col) > max_tem)
			{
				num_grid.push_back(all_row_col(i_row, i_col));
				double tem_ = all_row_col_mean(i_row, i_col) / all_row_col(i_row, i_col);
				result_jz.push_back(make_pair(0 + i_col*x_resolution + x_resolution / 2, tem_));
				if (all_row_col(i_row, i_col) > min_num_threshold)
				{
					result_.push_back(make_pair(0 + i_col*x_resolution + x_resolution / 2, tem_));
				}
			}
		}
	}
	if (line_num!=-1)
	{
		result_.clear();
		vectoridx_;
		vector_sort(num_grid, idx_);
		if (result_jz.size() < line_num)
		{
			line_num = result_jz.size();
		}
		for (int i_ = 0; i_ < line_num; i_++)
		{
			result_.push_back(result_jz[idx_[i_]]);
		}
	}
	for (int i_hough = 0; i_hough < result_.size(); i_hough++){
		B_.push_back(result_[i_hough].second / sin(result_[i_hough].first));
		K_.push_back(-cos(result_[i_hough].first) / sin(result_[i_hough].first));
	}
}
void HOUGH_LINE::draw_hough_line(){
	visualization::PCLPlotter *plot_line(new visualization::PCLPlotter);
	plot_line->setBackgroundColor(1, 1, 1);
	plot_line->setTitle("line display");
	plot_line->setXTitle("x");
	plot_line->setYTitle("y");
	vectorx_, y_;
	for (int i_point = 0; i_point < point_num; i_point++)
	{
		x_.push_back(cloud->points[i_point].x);
		y_.push_back(cloud->points[i_point].y);
	}
	for (int i_hough = 0; i_hough < result_.size(); i_hough++){
		std::vector func1(2, 0);
		func1[0] = result_[i_hough].second / sin(result_[i_hough].first);
		func1[1] = -cos(result_[i_hough].first) / sin(result_[i_hough].first);
		plot_line->addPlotData(func1, point_min.x, point_max.x);
	}
	plot_line->addPlotData(x_, y_, "display", vtkChart::POINTS);//X,Y均为double型的向量
	plot_line->setShowLegend(false);
	plot_line->plot();//绘制曲线
	//plot_line->spin();
}

//主函数，调用
#include "HOUGH_LINE.h"
int main()
{
	PointCloud::Ptr cloud(new PointCloud);
	pcl::io::loadPCDFile("C:\\Users\\admin\\Desktop\\222.pcd", *cloud);
	PointCloud::Ptr VOXEL;
	HOUGH_LINE hough;
	hough.setinputpoint(cloud);
	hough.VoxelGrid_(1.0, VOXEL);
	hough.draw_hough_spacing();
	vectorK_,B_;
	hough.HOUGH_line(181, 0.5, 400, K_, B_);//按阈值自动检测
	hough.HOUGH_line(181, 0.5, 400, K_, B_,3);//指定只选择极大值最大的3条直线
	hough.draw_hough_line();
	return 0;
}

提供的示例数据的霍夫空间展示：

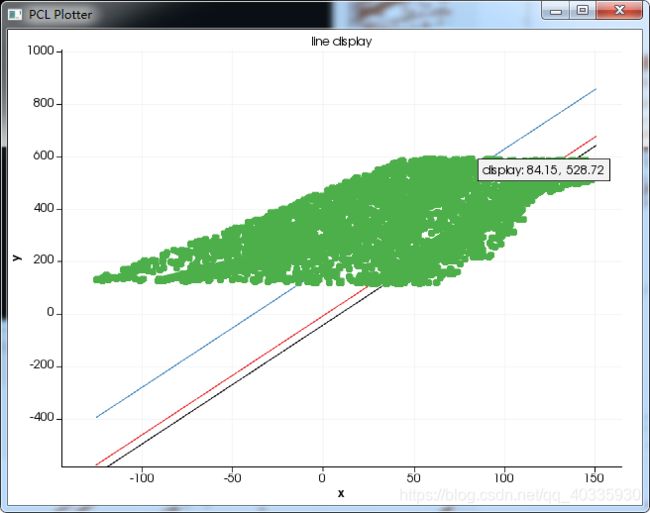
结果还是不错的，就是格网最低数量阈值不太好调，也是比较尴尬。

局部放大图：…

手动选择检测的条数：