word2vec

我的书：

淘宝购买链接
当当购买链接
京东购买链接

##word2vec是什么
word2vec（word to vector）是一个将单词转换成向量形式的工具。
##word2vec有什么用
word2vec适合用作序列数据的分类，聚类和相似度计算。有用作app下载推荐系统中的，也有用在推荐系统和广告系统上的，也可以用在机器人对话类别判决系统上。
###音乐推荐系统
基本思想是，现有的算法推荐音乐时，虽然现在的推荐系统要比以前好，但是总是不能让人满意；这里的核心思想就是让每一位音乐用户做为音乐推荐系统的歌单推荐源。我们假设$u_x,x=1,2,...$是user1，user2 …，假设$m_{x11},m_{x12},...$，m是music歌曲名。
$u1:m_{x11},m_{x12}...$，第一位用户听的超过30秒的歌单顺序排列
$u2:m_{x21},m_{x22}...$，第二位用户听的超过30秒的歌单顺序排列
我们把数百万个用户近两周听的数据按如下方式整理，每个用户歌单里的歌曲占一行，行内以空格分格，方便pandas数据处理。
把每一首歌曲看成是单词，这里要把歌曲像词一样转换成向量表示。
默认用户是理智的，
1.听超过30秒的歌曲是其喜欢的歌曲，当然也可以设置成60秒，以进一步筛选数据，
2.偶尔出现收听了超过30秒的歌曲并不是喜欢的歌曲，但是这中情况要远远小于喜欢的用户数。
3.我们可能能够拿到用户的年龄，地域等其它信息，这可以做为另一个维度的进一步帅选。
基于上述两点假设后，根据CBOW方法，进行歌曲的向量化映射，和训练，我们将最近一个月收听的歌曲名做为分词，歌曲名的序列组合做为词向量，训练得到的DNN模型。
这样在用户根据用户收藏的音乐或是用户指定的音乐，就可以根据其它用户的数据预测其应该喜欢收听的下一首歌曲。对新出的歌曲具有很好的适应性，过早的历史数据不会影响到当前的预测。
每两周一次的训练和上线，这类任务全部可以做自动化运维和部署实现，不需要人工干预。
###机器人对话类别解析
在人机对话的机器人系统中，要区分是音乐类，资讯类，翻译甚至对话聊天类的类别。由于类别这么多，很难一个公司做好上面的每一个类别的语义解析，尤其是开放式聊天类，虽然类似alpha go的强化学习方法被用户开放式聊天，但是聊天系统还是有一些第三方公司提供更好的体验。
好了问题来了，如果接入了第三方公司，出于对用户数据保护的角度，机器人公司并不想把所有的用户语音数据传输给第三方公司，且就算传给第三方公司，类似与家电控制/音乐等类别也无法解析。
机器人公司早期类别少依靠规则方式逐条增加，而这随着类别和用户表达方式的变化，难度越来越大，几乎到了更改一个规则，则对其它规则会有影响，并且规则的优先级会导致每条语句都做一次重新的判断，无法根据前几句的话进行有效的上下文联合判断。
使用word2vec是一个不错的解决思路。
##word2vec算法
上面说了这么好用，其理论还是要分析一下。首先这是一个逻辑回归（分类）问题，使用最大似然估计。
在已知历史单词$\mathbf{h}$，要最大化下一个单词$w_t$出现的概率，使用softmax函数做分类，则问题的数学描述如下：
$$P(w_t|\mathbf{h})=softmax(score(w_t,h))=\frac{\exp score(w_t,h)}{{\sum }_{w^{{}^{\prime }}\in V}\exp score(w^{{}^{\prime }},h)}$$
这里$score(w_t,\mathbf{h})$计算上下文是$\mathbf{h}$时单词是$w_t$的概率，显然上面的除法和指数计算是比较耗时，那么能否进行简化，答案就是取对数，将目标函数转换如下：
$$J_{ML}=\log P(w_t|\mathbf{h})=score(w_t,\mathbf{h})-\log (\sum _{w^{{}^{\prime }}\in V}\exp score(w^{{}^{\prime }},h))$$

假设我们的上下文是基于两个单词的，则根据the cat sits on the mat,将得到如下的训练样本。

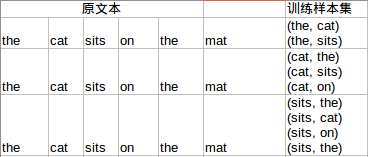
上面只罗列了CBOW下的样本集。神经网络的结构如下。

####输入层
上述过程可以描述如下：
1.首先将所有的单词做one-hot映射，这把每一个单词映射到权重矩阵的一行，这每一行对应于该单词的特征向量，

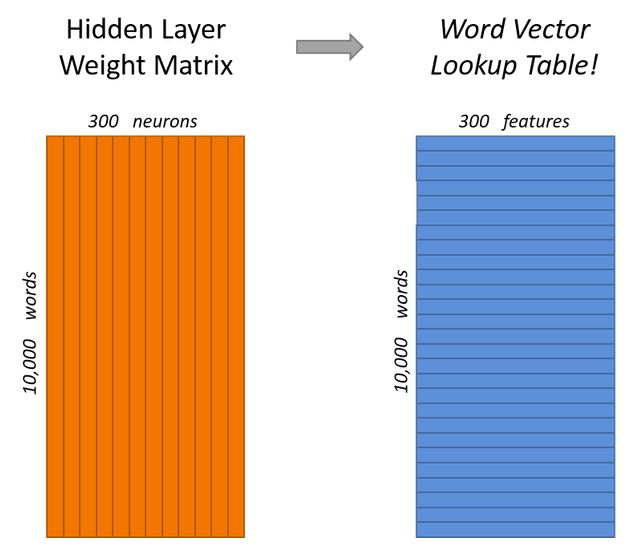
这里左侧竖条是权重矩阵，对应于上图神经网络的权重
2.右侧蓝色方框的每一行都是一个单词的特征，把上图hidden layer linear neurons旋转90°就是其表示。
这里已经说明了如何从单词映射到特征向量。
####输出层
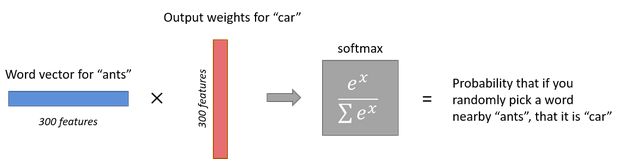
输入层使用softmax逻辑回归进行分类。
1.输出层输出的值累加和等于1，每一个神经元的值介于0~1
2.从单词特征向量和输出权重矩阵相乘得到softmax输出，由于输入特征向量是300维的，softmax输出预测的单词数量是和输入一致的，那么可以得出输出权重矩阵将是30010000维的，这一过程如下：

###计算量
上面给了两个矩阵：隐藏层权重矩阵和输出层权重矩阵，它们元素的个数是30010,000=3,000,000个，在一次训练中都需要对这么多元素递归求梯度并跟新这些参数，显然对这么小的规模计算量将是难以承受的，针对减小计算量提出了很多方法。接下来以negative sampling为例说明。该算法的核心思想是：既然一次跟新所有的权重系数带来的计算量暴增是无法接受的，那么能否一次训练中只跟新部分参数，这样的计算算会小很多，这种方法的计算将缩减到原计算量的$(k+1)/N$，其中$K$负样本的数量。N是分类器输出的种类数量，也就是输入单词的向量。试想一下，如果$k+1=20$，而$N=10000$，减少的计算量还是非常客观的，这使得在我的个人PC上编译的时间比编译安卓的时间少很多。使用gpu时间将进一步缩减。
###negative-sampling

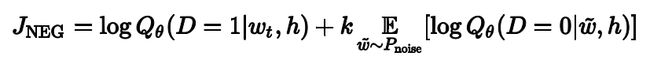
这是谷歌官网给出的简化计算后的目标函数，这里要估计的是$\theta$参数，$w_t$是目标单词，$k$是假目标单词$\tilde{w}$的数量。这一过程如下：

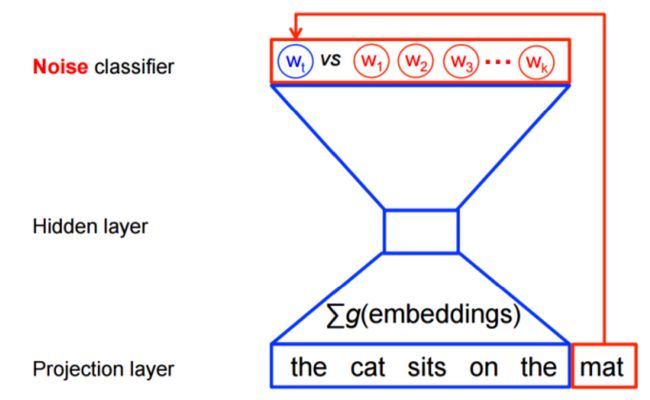
红色的圈是噪声干扰，总数是$k$。其它字符的意义不变。这里把多分类问题转换成了二分类问题。$Q_{\theta }(D=1|w,\mathbf{h})$是在文本集合$D$观测到上下文$\mathbf{h}$中观测到$w$的二分类逻辑回归问题。这一个算法是Noise-contrastive estimation（NCE）的一个特例，在tensorflow中使用tf.nn.nce_loss().
###Skip-gram 模型

the quick brown fox jumped over the lazy dog

则可得label样本集

(quick, the), (quick, brown), (brown, quick), (brown, fox), ...

则在第$t$次，根据quick预测将会出现的单词时，则损耗函数变为：
$J_{NEG}^{(t)}=\log Q_{\theta }(D=1|the,quick)+\log Q_{\theta }(D=0|sheep,quick)$
该目标函数的意义是观测到正确的词和错误词的代价函数。这里使用了NCE算法。见后文。
##tensorflow实现
谷歌的tensorflow官网上有非常详细的练习，这里就不粘贴代码了。强调一个图的概念。
###构建计算图
用媒体的化“构建神经元网络”，用google的话“构建计算图”，看来谷歌比较务实，这里的计算图离真实的生物神经网络还差十万八千里。

embeddings = tf.Variable(
    tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0))

nce_weights = tf.Variable(
  tf.truncated_normal([vocabulary_size, embedding_size],
                      stddev=1.0 / math.sqrt(embedding_size)))
nce_biases = tf.Variable(tf.zeros([vocabulary_size]))

##NCE算法
假设一个随机向量$X\in {\mathbb{R}}^n$，其真实概率密度函数是$p_d(\cdot )$，该模型的估计概率密度函数记作$p_m(\cdot ;\theta )$，其中$\theta$是一个向量参数。可以找到一个$p_d(\cdot )=p_m(\cdot ;{\theta }^{\ast })$,NCE算法就是为了找到估计${\theta }^{\ast }$的方法。
首先$\hat{\theta }$的任意一个解必须满足归一化，即：
$$\int p_m(\mathbf{u};\hat{\theta })d\mathbf{u}=1$$
以$\mathbf{X}=({\mathbf{X}}_1,..,{\mathbf{X}}_T)$为观测向量集,$\mathbf{Y}=({\mathbf{Y}}_1,..,{\mathbf{Y}}_T)$为分布是$p_n(\cdot )$的伪造（noise）的观测数据集。则目标函数变为：
$$J_T(\theta )=\frac{1}{2T}\sum _t\ln [h({\mathbf{X}}_t;\theta )]+\ln [1-h({\mathbf{y}}_t;\theta )]$$
$$h(\mathbf{u};\theta )=\frac{1}{1+\exp [-G(\mathbf{u};\theta )]}$$
$$G(\mathbf{u};\theta )=\ln p_m(\mathbf{u};\theta )-\ln p_n(\mathbf{u})$$
设$U=({\mathbf{u}}_1,...,{\mathbf{u}}_{2T})$是观测向量$\mathbf{X}$和噪声向量$\mathbf{Y}$的混合数据集。对每一个观测数据${\mathbf{u}}_t$和二元类别$C_t$：
$C_t=1,如果{\mathbf{u}}_t\in X$
$C_t=0,如果{\mathbf{u}}_t\in Y$
则有：
$p(\mathbf{u}|C=1;\theta )=p_m(\mathbf{u};\theta )$
$p(\mathbf{u}|C=0;\theta )=p_n(\mathbf{u};\theta )$
则可推得后验概率：
$$P(C=1|\mathbf{u};\theta )=\frac{p_m(\mathbf{u};\theta )}{p_m(\mathbf{u};\theta )+p_n(\mathbf{u})}=h(\mathbf{u};\theta )$$
$$P(C=0|\mathbf{u};\theta )=1-h(\mathbf{u};\theta )$$
由此可得对数似然：
$$J_n(\theta )=\sum _t\ln P(C_t=1|{\mathbf{x}}_t;\theta )+\sum _t\ln P(C_t=0|{\mathbf{y}}_t;\theta )=\sum _t\ln [h({\mathbf{X}}_t;\theta )]+\sum _t\ln [1-h({\mathbf{y}}_t;\theta )]$$
对于negativesample

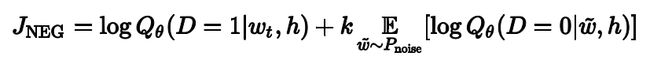
这里由于观测到的词$w_t$是确定的，所以$\sum$就一项，就是左侧的表示，而右侧公式k就是求和。