B-P反向传播网络算法的R实现(1)
一、B-P反向传播网络算法的R实现
在R中,B-P反向传播网络算法的实现主要集中在neuralnet和nnet这两个包中,首先我们先来学习使用neuralnet包。
install.packages(‘neuralnet’)
library(neuralnet)
该包中的neuralnet()函数可实现传统B-P反向传播网络弹性B-P网络的二分类建模与回归建模。函数调用公式如下:
neuralnet(formula, data, hidden = 1, threshold = 0.01,stepmax = 1e+05,
rep = 1, startweights = NULL, err.fct = “sse”,linear.output = TRUE,
learningrate=NULL,algorithm = “rprop+”)
hidden:用于指定隐层数和隐节点个数,默认值为1(即为1个隐层和1个隐节点),若hidden=c(3,2,1),则表示第1至第3个隐层分别包含3,2,1个隐节点
threshold:用于指定迭代停止条件,当权重的最大调整量小于指定值(默认0.01)时迭代终止
stepmax:同样用于指定迭代停止条件,当迭代次数达到指定次数(默认100000次)时迭代终止
err.fct:用于指定损失函数L的形式,"sse"表示损失函数为误差平方,"ce"表示为交互熵
linear.output:取值为TRUE或FALSE,分别表示输出节点的激活函数为线性函数(用于线性回归预测)还是非线性函数(默认sigmoid函数),在B-P中为FALSE
learningrate:学习率,当参数algorithm取值为’backpop’时需制定该参数为一个常数,否则学习率就是一个动态变化的量
algorithm:用于指定算法,"backpop"为传统B-P算法,"rprop+"或"rprop-“为弹性B-P算法,分别表示采用权重回溯或不回溯,不回溯将加速收敛(默认为"rprop+”)
除此之外,neuralnet()函数还有其他参数可供使用,具体内容可查看相关文档。
neuralnet()函数在实际应用后会返回一个包含众多计算结果的列表,主要内容包括:
response:各观测输出变量的实际值
• net.result:各观测输出变量的预测值(回归预测值或预测类别的概率)
• weights:各个节点的权重值列表
• result.matrix:终止迭代时各个节点的权重,迭代次数,损失函数值和权重的最大调整量
• startweights:各个节点的初始权重(初始权值为在(-1,+1)的正态分布随机数)
• 在明确了函数的基本用法后,接下来我们进行实际应用的学习,首先导入数据:
• > library(readxl)
consumer_data <- read_excel(‘consumer_data.xlsx’)
dim(data)
[1] 431 4
head(consumer_data)
BP模型构建
BP_model <- neuralnet(Purchase~Age+Gender+Income,data=consumer_data,
hidden=2,err.fct = ‘ce’,linear.output = FALSE)
• # 查看模型的连接权重与其他信息
BP_modelKaTeX parse error: Expected 'EOF', got '#' at position 21: …t.matrix • #̲ 查看连接权重列表 BP_m…weights
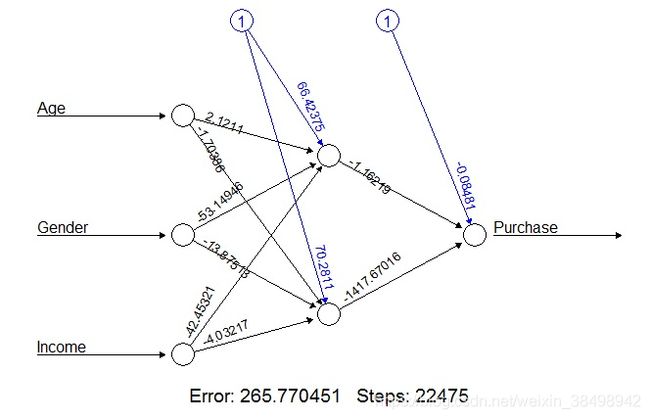
可视化神经网络
plot(BP_model)
评价输入变量的重要性
在算法的实际应用中,很多时候我们都需要明确哪些输入变量对输出变量的预测更为重要,而神经网络中的权重仅作为节点的连接强度测度,它是无法直观揭示输出变量的重要性的。为此,Neuralnet函数中提供了广义权重(Generalize Weight)用于测度解释变量的重要性。第i个输入变量的广义权重则定义为:
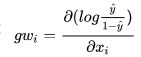
这是对数优势函数的偏导数,将观测值带入,计算第i个输入变量在第j个输出变量处的广义权重取值。从该式中可见,若第i个输入变量在所有观测值处的偏导数几乎为0,则表明该变量取值的变化不对对数优势产生影响,这也就意味着对输出变量影响是很小的。