算法基础:常用的排序算法知识笔记
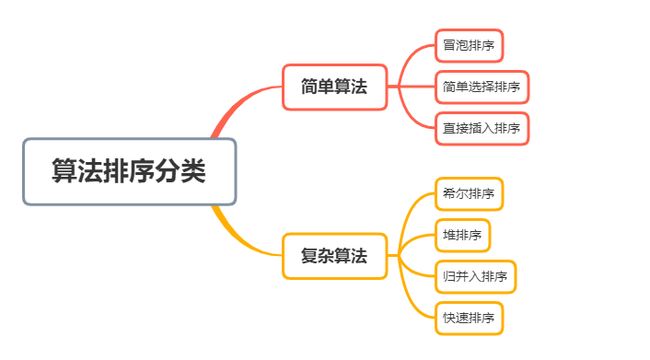
1、算法外排序分类
2、冒泡排序
冒泡排序(Bubble Sort)属于交换排序,它的原理是:循环两两比较相邻的记录,如果反序则交换,直到没有反序的记录为止。
实现算法:
/**
* 冒泡排序优化后的算法
* 设置一个标记来标志一趟比较是否发生交换
* 如果没有发生交换,则数组已经有序
*/
void bubbleSort(SqList *L){
int i,j;
int flag = true; // flag 用来作为标记
for (i = 1; i < L->length && flag; i++) {
// 若flag为true 则说明数据交换过,否则没交换过(数组已经有序) 则停止循环
flag = false;
for (j = L->length - 1; j >= i; j--) {
if (L->r[j] > L->r[j+1]) {
swap(L, j, j+1);
flag = true; // 如果有数据交换 flag为true
}
}
}
}
3、简单选择排序
简单选择排序法(Simple Selection Sort)是通过n-i次关键字间的比较,从n-i+1个记录中选出关键字最小的记录,并和第i(1<=i<=n)个记录交换。
原理是:每一次从无序数据组的数据元素中选出最小(或最大)的一个元素,存放在无序数组的开始位置,随着无序数组元素减少,有序组元素增加,直到全部待排序的数据元素完全排完。
/**
* 简单选择排序算法
*/
void selectSort(SqList *L){
int i, j, min;
for (i = 1; i < L->length; i++) {
min = i; // 将当前下标定义为最小值下标
for (j = i + 1; j <= L->length; j++) {
if (L->r[min] > L->r[j])
min = j;
}
if (i != min) // 若min不等于 i 说明找到最小值, 交换
swap(L, i, min);
}
}
4、直接插入排序
直接插入排序(Straight Insertion Sort)的是将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录增1的有序表。
原理:将一个记录插入到一个已经排序好的表中,得到一个记录增加1的有序表。并且它把当前元素大的记录都往后移动,用以腾出“自己”该插入的位置。当n-1趟插入完成后就是需要的有序序列。
/**
*直接插入排序算法
*/
void InsertSort(SqList *L){
int i, j;
for (i = 2; i < L->length; i++) {
if (L->r[i] < L->r[i-1]) { // 需要将 L->r[i] 插入有序子表
L->r[0] = L->r[i]; // 设置哨兵
for (j = i-1; L->r[j] > L->r[0]; j++)
L->r[j+1] = L->r[i]; // 记录后移
L->r[j+1] = L->r[0]; // 插入到正确位置
}
}
}
5、希尔排序
希尔排序是对直接插入排序的改进排序算法。希尔排序又叫缩小增量排序。
原理:希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。属于不稳定排序算法。
/**
* 希尔排序算法
*/
void shellSort(SqList *L){
int i,j;
int increment = L->length; // 增量初始值等于排序记录
do {
increment = increment /3 +1; // 增量序列
for (i = increment + 1; i < L->length; i++) {
if (L->r[i] < L->r[i-increment]) { // 需要将 L->r[i] 插入有序增量子表
L->r[0] = L->r[i]; // 用哨兵暂时存放 L->r[i]
for (j = i - increment; i >0 && L->r[0] < L->r[j]; j -= increment)
L->r[j+increment] = L->r[j]; // 记录后移, 查找插入位置
L->r[j+increment] = L->r[0]; // 插入
}
}
} while (increment > 1); // 增量不大于 1 时停止循环
}
6、堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
算法过程描述
1、将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
2、将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
3、由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
堆排序是一种不稳定的排序方法。
/**
* 已知 L->r[s..m] 中记录的关键字除L->r[s]之外均满足堆的定义
* 该函数调整L->r[s] 的关键字,使L->r[s..m]成为一个大顶堆
*/
void HeadAdjust(SqList *L, int s, int m){
int temp, j;
temp = L->r[s];
for (j = 2 *s; j <= m; j *= 2) { // 沿关键字较大的孩子结点向下筛选 这里循环的条件j从 2*s 开始是因为利用了二叉树的性质5:由于这颗是完全二叉树,当前节点序号是 s ,其左孩子的序号一定是 2s, 右孩子的序号一定是 2s+1,它们的孩子当然也是以 2 的位数序号增加,因此 j 变量才这样循环。
if (j < m && L->r[j] < L->r[j+1]) // 1. j < m 说明它不是最后一个节点 2. L->r[j] < L->r[j+1]) 说明左孩子小于右孩子
j++; // j 为关键字中较大的记录的下标
if (temp >= L->r[j])
break; // rc应插入在位置s上
L->r[s] = L->r[j];
s = j;
}
L->r[s] = temp; // 插入
}
/**
* 对顺序表L进行堆排序
*/
void HeapSort(SqList *L){
int i;
for (i = L->length / 2; i>0; i--) // 把L中的r构建成一个大顶堆
HeadAdjust(L, i, L->length);
for (i = L->length; i > 1; i--) {
swap(L, 1, i); // 将堆顶记录和当前未经排序子序列的最后一个记录交换
HeadAdjust(L, 1, i-1); // 将L->r[1..i-1]重新调整为大顶堆
}
}
7、归并排序
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
实现原理(递归实现):
1、将序列平均分成两部分
2、分别对这两部分用递归来归并
3、将这两部分归并到一起
算法示例
#p.归并排序(递归实现)
/**
* 将有序的 SR[i..m] 和 SR[m+1..n]归并为有序的 TR[i..n]
*/
void Merge(int SR[], int TR[], int i, int m, int n){
int j, k, l;
for (j = m+1, k = i; i <= m && j <= n; k++) { // 将SR中记录有小到大归并入TR
if (SR[i] < SR[j])
TR[k] = SR[i++];
else
TR[k] = SR[j++];
}
if (i <= m) {
for (l=0; l <= m-i; l++)
TR[k+l] = SR[i+l]; // 将剩余的SR[i..m]复制到TR
}
if (j <= n) {
for (l=0; l <= n-j; l++)
TR[k+l] = SR[j+l]; // 将剩余的SR[j..n]复制到TR
}
}
/**
*将SR[s..t]归并排序为TR1[s..t]
*/
void MSort(int SR[], int TR1[], int s, int t){
int m;
int TR2[MAXSIZE+1];
if (s == t) {
TR1[s] = SR[s];
}else{
m = (s+t)/2; // 将SR[s..t]平分为SR[s..m]和SR[m+1..t]
MSort(SR, TR2, s, m); // 递归将SR[s..m]归并为有序的TR2[s..m]
MSort(SR, TR2, m+1, t); // 递归将SR[m+1..t]归并为有序的TR2[m+1..t]
Merge(TR2, TR1, s, m, t); // 将TR2[s..m]和TR2[m+1..t]归并到TR1[s..t]
}
}
/**
* 对顺序表L作归并排序
*/
void MergeSort(SqList *L){
MSort(L->r, L->r, 1, L->length);
}
归并排序是一种比较占内存,但是效率高且稳定的算法。
8、快速排序
实现原理:
选取一个关键字,放到一个位置,使得它的左边的值都比它小,右边的值都比它大,这个关键字叫做枢轴(pivot)
然后分别对左边和右边进行排序。
#p快速排序
/**
* 交换顺序表 L 中子表的记录,使轴记录到位,并返回其所在位置
* 此时在它之前的记录均不大于它,在它之后的记录均不小于它
*/
int partition(SqList * L, int low, int high){
int pivotkey;
pivotkey = L->r[low]; // 用子表的第一个记录作为枢轴记录
while (low < high) { // 从表的两端交替地向中间扫描
while (low < high && L->r[high] >= pivotkey)
high --;
swap(L, low, high); // 将比枢轴小的记录交换到低端
while (low < high && L->r[low] <= pivotkey)
high++;
swap(L, low, high); // 将比枢轴大的记录交换到高端
}
return low; // 返回枢轴所在位置
}
/**
* 对顺序表 L 中的子序列 L->r[low..high] 作快速排序
*/
void QSort(SqList *L, int low, int high){
int pivot;
if (low < high) {
pivot = Partition(L, low, high); // 将L->r[low..high]一分为二,算出枢轴值pivot
QSort(L, low, pivot-1); // 对 低子表递归排序
QSort(L, pivot+1, high); // 对 高子表递归排序
}
}
/**
* 对顺序表 L 作快速排序
*/
void QuickSort(SqList *L){
QSort(L, 1, L->length);
}
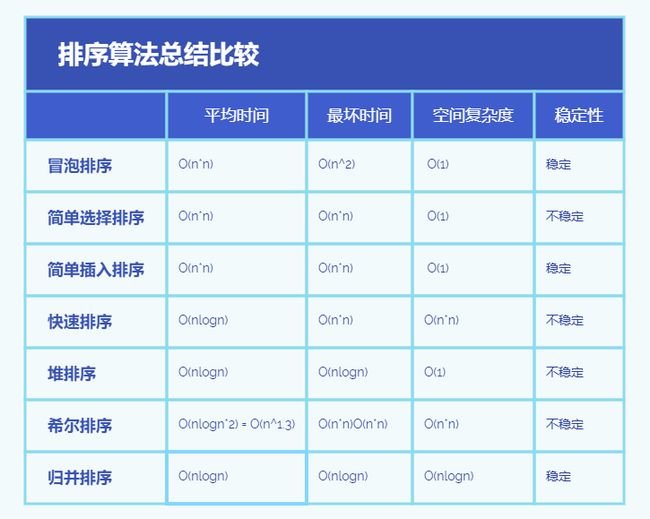
9、排序算法比较
10、排序算法总结
10.1 内部排序
1、排序的记录数量较少是,可以考虑插入排序和简短选择排序。如果记录本身信息量较大时,建议选用选择排序。
2、如果待排序记录按关键字基本有序,适合采用冒泡排序或直接插入排序
3、若 排序记录较大,可以选择快速排序、堆排序或归并排序。目前快速排序被认为最好的排序方法。
10.2 外部排序
外部排序就是针对大型文件的排序。常用的外部排序方法是归并排序。
IT技术分享社区
个人博客网站:https://programmerblog.xyz
![]()
文章推荐程序员效率:画流程图常用的工具程序员效率:整理常用的在线笔记软件远程办公:常用的远程协助软件,你都知道吗?51单片机程序下载、ISP及串口基础知识硬件:断路器、接触器、继电器基础知识