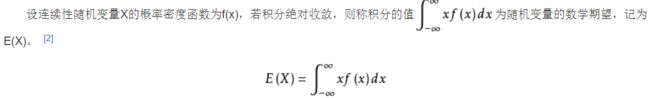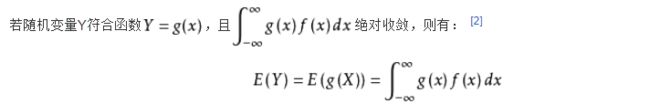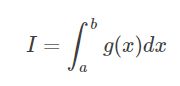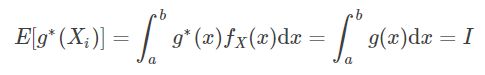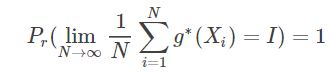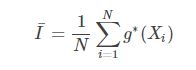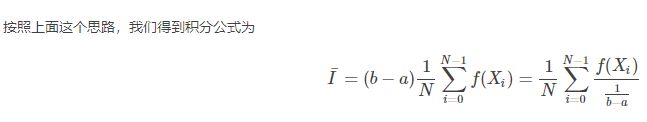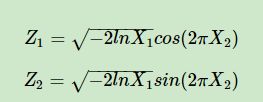算法学习系列（MCMC）：马尔可夫链和蒙特卡洛方法
马尔科夫链蒙特卡罗（Markov Chain Monte Carlo，以下简称MCMC）作为一种随机采样方法，在机器学习，深度学习以及 NLP 等领域都有广泛的应用，是很多复杂算法求解的基础。比如分解机(Factorization Machines，FM)推荐算法，还有受限玻尔兹曼机（RBM），都用到了MCMC来做复杂运算的近似求解。
从名字我们可以看出，MCMC由两部分组成，马尔可夫链和蒙特卡洛方法。该方法将马尔科夫(Markov)过程引入到Monte Carlo模拟中，实现抽样分布随模拟的进行而改变的动态模拟，弥补了传统的蒙特卡罗积分只能静态模拟的缺陷。想要弄明白MCMC，首先就得搞明白马尔可夫链和蒙特卡罗方法的原理。
马尔可夫链
概念解释
马尔可夫链是满足马尔科夫性质的随机过程。马尔可夫链X1, X2 ... Xn,描述了一个状态序列，其中每个状态值取决于前一个状态（马尔可夫链在状态空间内的取值称为状态）。常见地，马尔可夫链 
的下标集被称为“步”或“时间步（time-step）”。
马尔可夫链的数学定义为：
上式在定义马尔可夫性质该性质也被称为“无记忆性（memorylessness）”，即 t+1 步的随机变量在给定第t步随机变量后与其余的随机变量条件独立（conditionally independent）：
。在此基础上，马尔可夫链具有强马尔可夫性（strong Markov property），即对任意的停时（ t )（ stopping time），马尔可夫链在停时前后的状态相互独立 。
马尔可夫链示例
我们来看看下图这个马尔科夫链模型的具体的例子。
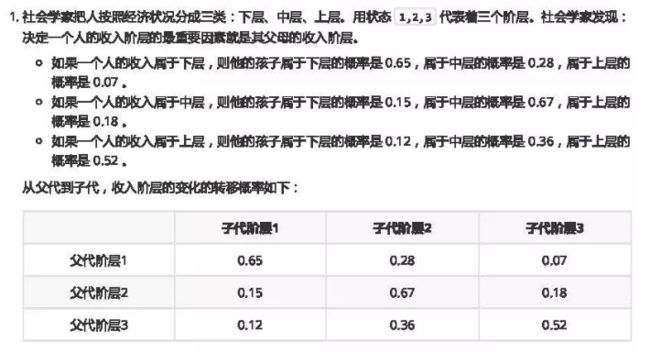
这个马尔科夫链是表示股市模型的，共有三种状态：牛市（Bull market）, 熊市（Bear market）和横盘（Stagnant market）。定义牛市、熊市、横盘的状态分别为0、1、2。
每一个状态都以一定的概率转化到下一个状态。比如，牛市以0.025的概率转化到横盘的状态。这个状态概率转化图可以以矩阵的形式表示。如果我们定义矩阵阵P某一位置 P( i，j ) 的值为 P( j | i )，即从状态 i 变为状态 j 的概率。这样我们得到了马尔科夫链模型的状态转移矩阵为：
当这个状态转移矩阵P确定以后，整个股市模型就已经确定！
整个马尔可夫链模型的核心是状态转移矩阵P。那这个矩阵P有一些什么有意思的地方呢？接下来再看一下。
以股市模型为例，假设初始状态（牛市、熊市和横盘的概率分布）为 
，然后计算之后的状态（之后的状态。
import numpy as np
def markov():
init_array = np.array([0.1, 0.2, 0.7])
transfer_matrix = np.array([[0.9, 0.075, 0.025],
[0.15, 0.8, 0.05],
[0.25, 0.25, 0.5]])
restmp = init_array
for i in range(25):
res = np.dot(restmp, transfer_matrix)
print(i, "\t", res)
restmp = res
if __name__ == "__main__":
markov()
输出结果为：
从输出结果我们可以看出，从第20次开始，状态就开始收敛至 [0.624，0.312，0.0625]，如果我们换一个初始状态t_0，比如[0.2,0.3.0.5]，继续运行上面的代码，只是将init_array变一下，最后结果为：
到第20次的时候，又收敛到了[0.624，0.312，0.0625] 。不管我们的初始状态是什么样子的，只要状态转移矩阵不发生变化，当n→∞时，最终状态始终会收敛到一个固定值。
我们也看看这个状态转移矩阵P的幂次方有什么有意思的地方？代码如下：
import numpy as np
def matrixpower():
transfer_matrix = np.array([[0.9, 0.075, 0.025],
[0.15, 0.8, 0.05],
[0.25, 0.25, 0.5]])
restmp = transfer_matrix
for i in range(25):
res = np.dot(restmp, transfer_matrix)
print(i,"\n", res)
restmp = res
if __name__ == "__main__":
matrixpower()
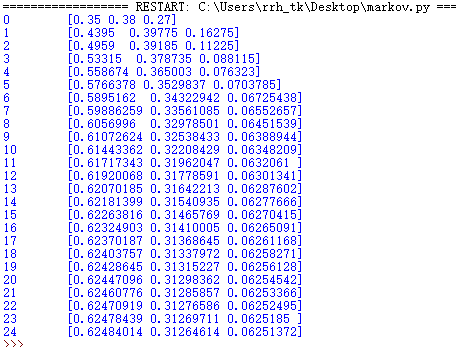
代码运行的结果：
0
[[0.8275 0.13375 0.03875]
[0.2675 0.66375 0.06875]
[0.3875 0.34375 0.26875]]
1
[[0.7745 0.17875 0.04675]
[0.3575 0.56825 0.07425]
[0.4675 0.37125 0.16125]]
2
[[0.73555 0.212775 0.051675]
[0.42555 0.499975 0.074475]
[0.51675 0.372375 0.110875]]
3
[[0.70683 0.238305 0.054865]
[0.47661 0.450515 0.072875]
[0.54865 0.364375 0.086975]]
4
[[0.685609 0.2573725 0.0570185]
[0.514745 0.4143765 0.0708785]
[0.570185 0.3543925 0.0754225]]
5
[[0.6699086 0.2715733 0.0585181]
[0.5431466 0.3878267 0.0690267]
[0.585181 0.3451335 0.0696855]]
6
[[0.65828326 0.28213131 0.05958543]
[0.56426262 0.36825403 0.06748335]
[0.5958543 0.33741675 0.06672895]]
7
[[0.64967099 0.28997265 0.06035636]
[0.5799453 0.35379376 0.06626094]
[0.60356362 0.33130471 0.06513167]]
8
[[0.64328888 0.29579253 0.06091859]
[0.59158507 0.34309614 0.06531879]
[0.60918588 0.32659396 0.06422016]]
9
[[0.63855852 0.30011034 0.06133114]
[0.60022068 0.33517549 0.06460383]
[0.61331143 0.32301915 0.06366943]]
10
[[0.635052 0.30331295 0.06163505]
[0.60662589 0.3293079 0.06406621]
[0.61635051 0.32033103 0.06331846]]
11
[[0.63245251 0.30568802 0.06185947]
[0.61137604 0.32495981 0.06366415]
[0.61859473 0.31832073 0.06308454]]
12
[[0.63052533 0.30744922 0.06202545]
[0.61489845 0.32173709 0.06336446]
[0.6202545 0.31682232 0.06292318]]
13
[[0.62909654 0.30875514 0.06214832]
[0.61751028 0.31934817 0.06314155]
[0.62148319 0.31570774 0.06280907]]
14
[[0.62803724 0.30972343 0.06223933]
[0.61944687 0.3175772 0.06297594]
[0.6223933 0.3148797 0.062727 ]]
15
[[0.62725186 0.31044137 0.06230677]
[0.62088274 0.31626426 0.062853 ]
[0.62306768 0.31426501 0.06266732]]
16
[[0.62666957 0.31097368 0.06235675]
[0.62194736 0.31529086 0.06276178]
[0.62356749 0.31380891 0.0626236 ]]
17
[[0.62623785 0.31136835 0.0623938 ]
[0.6227367 0.31456919 0.06269412]
[0.62393798 0.31347059 0.06259143]]
18
[[0.62591777 0.31166097 0.06242126]
[0.62332193 0.31403413 0.06264394]
[0.62421263 0.31321968 0.0625677 ]]
19
[[0.62568045 0.31187792 0.06244162]
[0.62375584 0.31363743 0.06260672]
[0.62441624 0.31303361 0.06255015]]
20
[[0.6255045 0.31203878 0.06245672]
[0.62407756 0.31334332 0.06257913]
[0.62456719 0.31289565 0.06253716]]
21
[[0.62537405 0.31215804 0.06246791]
[0.62431608 0.31312525 0.06255867]
[0.62467911 0.31279335 0.06252754]]
22
[[0.62527733 0.31224646 0.06247621]
[0.62449293 0.31296357 0.0625435 ]
[0.62476209 0.3127175 0.06252042]]
23
[[0.62520562 0.31231202 0.06248236]
[0.62462404 0.3128437 0.06253225]
[0.62482361 0.31266126 0.06251514]]
24
[[0.62515245 0.31236063 0.06248692]
[0.62472126 0.31275483 0.06252391]
[0.62486922 0.31261956 0.06251122]]
从第20次开始，结果开始收敛，并且每一行都为 [0.624，0.312，0.0625]。
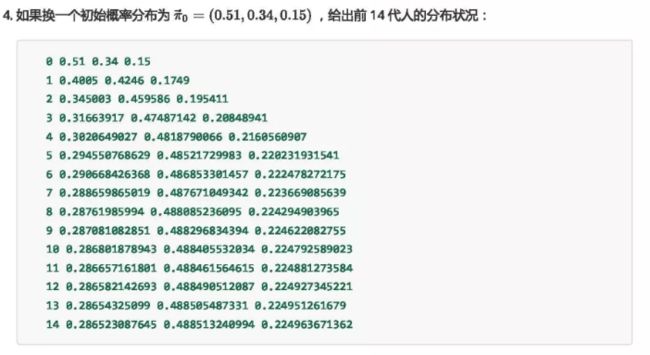
我们再来看一个例子：
平稳分布和收敛
蒙特卡罗方法大致可以粗略地分成两类：
一类是所求解的问题本身具有内在的随机性，借助计算机的运算能力可以直接模拟这种随机的过程。例如在核物理研究中，分析中子在反应堆中的传输过程。中子与原子核作用受到量子力学规律的制约，人们只能知道它们相互作用发生的概率，却无法准确获得中子与原子核作用时的位置以及裂变产生的新中子的行进速率和方向。科学家依据其概率进行随机抽样得到裂变位置、速度和方向，这样模拟大量中子的行为后，经过统计就能获得中子传输的范围，作为反应堆设计的依据。
另一种类型是所求解问题可以转化为某种随机分布的特征数，比如随机事件出现的概率，或者随机变量的期望值。通过随机抽样的方法，以随机事件出现的频率估计其概率，或者以抽样的数字特征估算随机变量的数字特征，并将其作为问题的解。这种方法多用于求解复杂的多维积分问题。
蒙特卡洛方法
概念解释
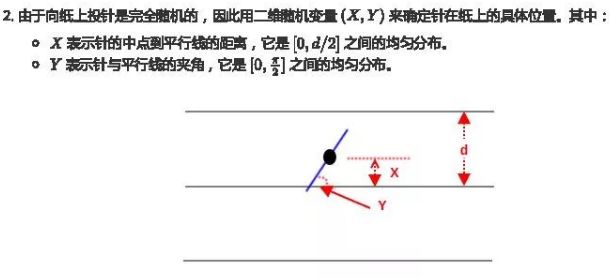
蒙特卡洛方法示例——布丰投针
蒙特卡洛方法示例——求积分
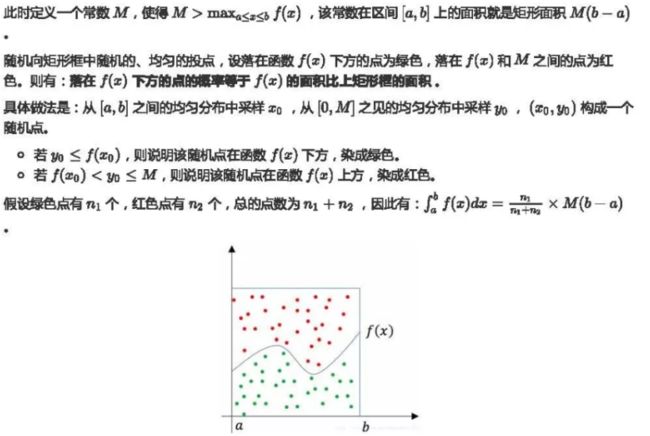
投点法
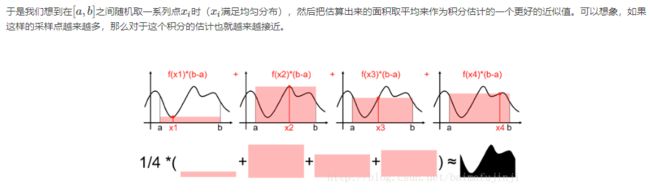
如下图所示，有一个函数f(x)，若要求它从a到b的定积分，其实就是求曲线下方的面积。
期望法（平均值法）
概念解释
期望法分析
假设要计算的积分如下：
其中被积函数 g(x) 在[a,b]内可积。如果选择一个概率密度函数为
的方式进行抽样（随机变量 X），并且满足
，原有的积分可以写成如下形式： 
：
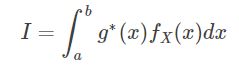
也就是说（强大数定律）：
我们令
我们再来梳理一下：
因而求积分的步骤如下：
在期望法求积分中
具体步骤变为：
期望法的直观解释：
其中的
就是均匀分布的PDF（或者PMF）。
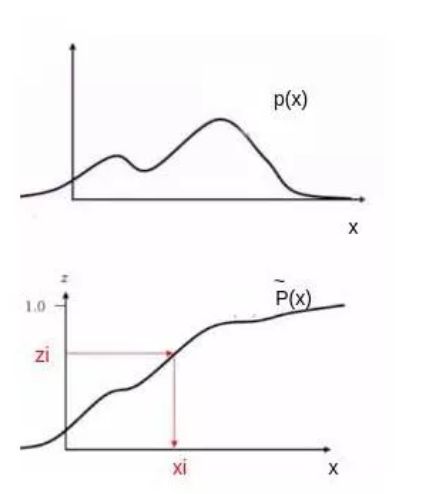
蒙特卡洛采样
采样问题的主要任务是：根据概率分布 p(x) ，生成一组服从分布的随机数 x1 ，x2 . . .，
均匀分布采样
对于常见的均匀分布 uniform(0,1) 是非常容易采样样本的，一般通过线性同余发生器可以很方便的生成(0,1)之间的伪随机数样本。而其他常见的概率分布，无论是离散的分布还是连续的分布，它们的样本都可以通过 uniform(0,1) 的样本转换而得。比如二维正态分布的样本 (Z1,Z2) 可以通过独立采样得到的 uniform(0,1) 样本对 (X1,X2) 通过如下的式子转换而得：
其他一些常见的连续分布，比如t分布，F分布，Beta分布，Gamma分布等，都可以通过类似的方式从uniform(0,1) 得到的采样样本转化得到。在python的numpy，scikit-learn等类库中，都有生成这些常用分布样本的函数可以使用。
通过均匀分布采样
如果累计分布函数无法计算，或者反函数难以求解，则该方法无法进行。
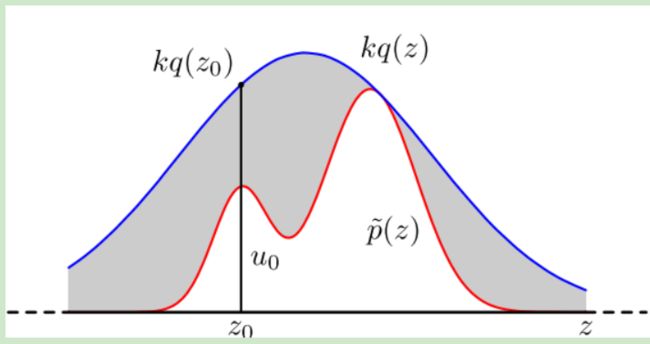
接受—拒绝采样
对于概率分布不是常见的分布，一个可行的办法是采用接受-拒绝采样来得到该分布的样本。既然 p(x)p(x) 太复杂在程序中没法直接采样，那么我设定一个程序可采样的分布 q(x) 比如高斯分布，然后按照一定的方法拒绝某些样本，以达到接近 p(x)分布的目的。
重复以上过程得到n个接受的样本 
，则最后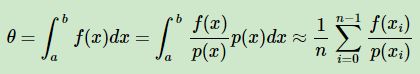
的蒙特卡罗方法求解结果为：
整个过程中，我们通过一系列的接受拒绝决策来达到用q(x)模拟p(x)概率分布的目的。
接受拒绝采样有时很难满足我们的概率分布样本集
（1）对于一些二维分布p(x,y)，有时候我们只能得到条件分布p(x|y)和p(y|x)和,却很难得到二维分布p(x,y)一般形式，这时我们无法用接受-拒绝采样得到其样本集。
（2）在高维的情况下会出现以下两个问题
