- 【心灵鸡汤】深度学习技能形成树:从零基础到AI专家的成长路径全解析
智算菩萨
人工智能深度学习
引言:技能树的生长哲学在这个人工智能浪潮汹涌的时代,深度学习犹如一棵参天大树,其根系深深扎入数学与计算科学的沃土,主干挺拔地承载着机器学习的核心理念,而枝叶则繁茂地延伸至计算机视觉、自然语言处理、强化学习等各个应用领域。对于初入此领域的新手而言,理解这棵技能树的生长规律,掌握其形成过程中的关键节点和发展阶段,将直接决定其在人工智能道路上能够走多远、攀多高。技能树的概念源于游戏设计,但在学习深度学习
- 【计算机毕业设计】基于Springboot的办公用品管理系统+LW
枫叶学长(专业接毕设)
Java毕业设计实战案例课程设计springboot后端
博主介绍:✌全网粉丝3W+,csdn特邀作者、CSDN新星计划导师、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和学生毕业项目实战,高校老师/讲师/同行前辈交流✌技术范围:SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、安卓app、大数据、物联网、机器学习等设计与开发。主要内容:
- 【TVM 教程】如何处理 TVM 报错
ApacheTVM是一个深度的深度学习编译框架,适用于CPU、GPU和各种机器学习加速芯片。更多TVM中文文档可访问→https://tvm.hyper.ai/运行TVM时,可能会遇到如下报错:---------------------------------------------------------------AnerroroccurredduringtheexecutionofTVM.F
- 【PaddleOCR】OCR文本检测与文本识别数据集整理,持续更新......
博主简介:曾任某智慧城市类企业算法总监,目前在美国市场的物流公司从事高级算法工程师一职,深耕人工智能领域,精通python数据挖掘、可视化、机器学习等,发表过AI相关的专利并多次在AI类比赛中获奖。CSDN人工智能领域的优质创作者,提供AI相关的技术咨询、项目开发和个性化解决方案等服务,如有需要请站内私信或者联系任意文章底部的的VX名片(ID:xf982831907)博主粉丝群介绍:①群内初中生、
- ImportError: /nvidia/cusparse/lib/libcusparse.so.12: undefined symbol: __nvJitLinkComplete_12_4
爱编程的喵喵
Python基础课程pythonImportErrortorchnvJitLink解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理解,而且能够帮助新手快速入门。 本文主要介绍了ImportError:/home/
- 【机器学习笔记 Ⅱ】11 决策树模型
巴伦是只猫
机器学习机器学习笔记决策树
决策树模型(DecisionTree)详解决策树是一种树形结构的监督学习模型,通过一系列规则对数据进行分类或回归。其核心思想是模仿人类决策过程,通过不断提问(基于特征划分)逐步逼近答案。1.核心概念节点类型:根节点:起始问题(最佳特征划分点)。内部节点:中间决策步骤(特征判断)。叶节点:最终预测结果(类别或数值)。分支:对应特征的取值或条件判断(如“年龄≥30?”)。2.构建决策树的关键步骤(1)
- 【机器学习笔记 Ⅱ】10 完整周期
机器学习的完整生命周期(End-to-EndPipeline)机器学习的完整周期涵盖从问题定义到模型部署的全过程,以下是系统化的步骤分解和关键要点:1.问题定义(ProblemDefinition)目标:明确业务需求与机器学习任务的匹配性。关键问题:这是分类、回归、聚类还是强化学习问题?成功的标准是什么?(如准确率>90%、降低10%成本)输出:项目目标文档(含评估指标)。2.数据收集(DataC
- 【机器学习笔记Ⅰ】13 正则化代价函数
正则化代价函数(RegularizedCostFunction)详解正则化代价函数是机器学习中用于防止模型过拟合的核心技术,通过在原始代价函数中添加惩罚项,约束模型参数的大小,从而提高泛化能力。以下是系统化的解析:1.为什么需要正则化?过拟合问题:当模型过于复杂(如高阶多项式回归、深度神经网络)时,可能完美拟合训练数据但泛化性能差。解决方案:在代价函数中增加对参数的惩罚,抑制不重要的特征权重。2.
- 【机器学习笔记Ⅰ】6 多类特征
巴伦是只猫
机器学习机器学习笔记人工智能
多类特征(Multi-classFeatures)详解多类特征是指一个特征(变量)可以取多个离散的类别值,且这些类别之间没有内在的顺序关系。这类特征是机器学习中常见的数据类型,尤其在分类和回归问题中需要特殊处理。1.核心概念(1)什么是多类特征?定义:特征是离散的、有限的类别,且类别之间无大小或顺序关系。示例:颜色:红、绿、蓝(无顺序)。城市:北京、上海、广州(无数学意义的大小关系)。动物类别:猫
- 图像分割技术详解:从原理到实践
lanjieying
本文还有配套的精品资源,点击获取简介:图像分割是图像处理领域将图像分解为多个区域的过程,用于图像分析、特征提取等。文章介绍了图像分割的原理,并通过一个将图像划分为2*4子块的示例,展示了如何使用Python和matplotlib库中的tight_subplot函数进行图像分割和展示。文章还探讨了图像分割在不同领域的应用,以及如何在机器学习项目中作为数据预处理步骤。1.图像分割基本概念在图像处理领域
- 机器学习笔记——支持向量机
star_and_sun
机器学习笔记支持向量机
支持向量机参数模型对分布需要假设(这也是与非参数模型的区别之一)间隔最大化,形式转化为凸二次规划问题最大化间隔间隔最大化是意思:对训练集有着充分大的确信度来分类训练数据,最难以分的点也有足够大的信度将其分开间隔最大化的分离超平面的的求解怎么求呢?最终的方法如下1.线性可分的支持向量机的优化目标其实就是找得到分离的的超平面求得参数w和b的值就可以了注意,最大间隔分离超平面是唯一的,间隔叫硬间隔1.1
- 【机器学习&深度学习】多分类评估策略
一叶千舟
深度学习【理论】深度学习【应用必备常识】大数据人工智能
目录前言一、多分类3大策略✅宏平均(MacroAverage)✅加权平均(WeightedAverage)✅微平均(MicroAverage)二、类比理解2.1宏平均(MacroAverage)2.1.1计算方式2.1.2适合场景2.1.3宏平均不适用的场景2.1.4宏平均一般用在哪些指标上?2.1.5怎么看macroavg指标?2.1.6宏平均值低说明了什么?2.1.7从宏平均指标中定位模型短板
- 【机器学习笔记Ⅰ】7 向量化
巴伦是只猫
机器学习机器学习笔记人工智能
向量化(Vectorization)详解向量化是将数据或操作转换为向量(或矩阵)形式,并利用并行计算高效处理的技术。它是机器学习和数值计算中的核心优化手段,能显著提升代码运行效率(尤其在Python中避免显式循环)。1.为什么需要向量化?(1)传统循环的缺陷低效:Python的for循环逐元素操作,速度慢。代码冗长:需手动处理每个元素。示例:计算两个数组的点积(非向量化)a=[1,2,3]b=[4
- 李宏毅2025《机器学习》第四讲-Transformer架构的演进
Transformer架构的演进与替代方案:从RNN到Mamba的技术思辨Transformer作为当前AI领域的标准架构,其设计并非凭空而来,也并非没有缺点。本次讨论的核心便是:新兴的架构,如MAMA,是如何针对Transformer的弱点进行改进,并试图提供一个更优的解决方案的。要理解架构的演进,我们必须首先明确一个核心原则:每一种神经网络架构,都有其存在的技术理由。CNN(卷积神经网络):为
- 条件概率:不确定性决策的基石
大千AI助手
人工智能Python#OTHER决策树算法机器学习人工智能条件概率概率论
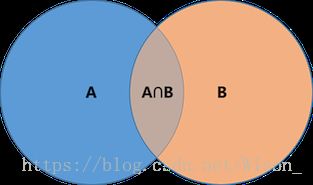
条件概率是概率论中的核心概念,用于描述在已知某一事件发生的条件下,另一事件发生的概率。它量化了事件之间的关联性,是贝叶斯推理、统计建模和机器学习的基础。本文由「大千AI助手」原创发布,专注用真话讲AI,回归技术本质。拒绝神话或妖魔化。搜索「大千AI助手」关注我,一起撕掉过度包装,学习真实的AI技术!一、定义与公式设(A)和(B)是两个随机事件,且(P(B)>0):条件概率(P(A\midB))表示
- 人工智能动画展示人类的特征
AGI大模型与大数据研究院
AI大模型应用开发实战javapythonjavascriptkotlingolang架构人工智能
人工智能,动画,人类特征,情感识别,行为模拟,机器学习,深度学习,自然语言处理1.背景介绍人工智能(AI)技术近年来发展迅速,已渗透到生活的方方面面。从智能语音助手到自动驾驶汽车,AI正在改变着我们的世界。然而,尽管AI技术取得了令人瞩目的成就,但它仍然难以完全模拟人类的复杂行为和特征。人类的特征是多方面的,包括情感、认知、社交和创造力等。这些特征是人类区别于其他生物的重要标志,也是人类社会文明发
- 《支持向量机(SVM)在医疗领域的变革性应用》
CodeJourney.
支持向量机算法机器学习
在医疗科技日新月异的今天,先进的数据分析与机器学习技术正逐渐成为提升诊疗水平、助力医学研究的关键力量。支持向量机(SVM),凭借其独特的优势,在医疗这片复杂且对精准度要求极高的领域崭露头角,带来诸多令人瞩目的应用成果。一、疾病诊断:癌症早期筛查的“火眼金睛”癌症,作为全球健康的“头号杀手”,早期诊断对提升患者生存率意义非凡。在乳腺癌筛查领域,SVM发挥着重要作用。医疗科研人员收集大量乳腺组织的影像
- 机器学习20-线性网络思考
坐吃山猪
机器学习机器学习人工智能线性网络
机器学习20-线性网络思考针对线性网络的基础问题,使用基础示例进行解释1-核心知识点1-线性模型家族的线性回归和逻辑回归分别是什么,线性模型家族还有没有其他的模型线性模型家族是一系列基于线性假设的统计模型,它们假设因变量和自变量之间存在线性关系。线性模型家族中的两个最常见模型是线性回归和逻辑回归。线性回归(LinearRegression):线性回归是一种用于预测连续因变量的模型。它假设因变量yy
- 机器学习18-强化学习RLHF
坐吃山猪
机器学习机器学习人工智能
机器学习18-强化学习RLHF1-什么是RLHFRLHF(ReinforcementLearningfromHumanFeedback)即基于人类反馈的强化学习算法,以下是详细介绍:基本原理RLHF是一种结合了强化学习和人类反馈的机器学习方法。传统的强化学习通常依赖于预定义的奖励函数来指导智能体的学习,而RLHF则通过引入人类的反馈来替代或补充传统的奖励函数。在训练过程中,人类会对智能体的行为或输
- 机器学习19-Transformer和AlexNet思考
坐吃山猪
机器学习机器学习transformer人工智能
Transformer和AlexNet思考关于Transformer和AlexNet发展的一些思考1-核心知识点Word2Vec的作用是什么,和Transformer的诞生有什么关系吗?AlexNet的主要核心思路是什么,为什么表现那么好?现在有什么比AlexNet更优秀的算法2-思路整理1-Word2Vec的作用是什么,和Transformer的诞生有什么关系吗?Word2Vec的作用Word2
- 机器学习21-线性网络思考
坐吃山猪
机器学习机器学习人工智能线性网络
机器学习21-线性网络思考针对线性网络的发展问题,进行补充学习1-核心知识点1-传统机器学习针对线性分类算法求解的方式有哪些?请详细列举不同的算法对应的损失函数和计算思路在传统机器学习中,线性分类算法是一种非常重要的方法,用于将数据划分为不同的类别。以下是几种常见的线性分类算法,包括它们的损失函数和计算思路:1.感知机(Perceptron)损失函数感知机的损失函数是基于误分类点的,其目标是最小化
- Spring AI 第二讲 之 Chat Model API 第五节HuggingFace Chat
HuggingFaceInferenceEndpoints允许您在云中部署和提供机器学习模型,并通过API对其进行访问。开始使用有关HuggingFaceInferenceEndpoints的更多详细信息,请访问此处。前提条件添加spring-ai-huggingface依赖关系:org.springframework.aispring-ai-huggingface获取HuggingFaceAPI
- Python设置国内镜像教程
wh3933
python开发语言
####引言Python是一种广泛使用的高级编程语言,用于各种编程任务,从简单的脚本到复杂的机器学习算法。在安装Python包时,通常需要从Python包索引(PyPI)下载。由于网络原因,直接从PyPI下载可能速度较慢,因此,使用国内的镜像源可以显著提高下载速度。本文将详细介绍如何在Python中设置国内镜像。####文章目的本篇文章旨在指导用户如何将Python的包管理工具`pip`的默认源切
- 机器学习宝典——第6章
爱看烟花的码农
机器学习人工智能
第6章:聚类算法(Clustering)你好,同学!欢迎来到无监督学习的世界。与监督学习不同,这里的我们没有“标准答案”(标签),我们的目标是在数据中发现隐藏的、内在的结构。聚类算法就是实现这一目标的核心工具,它试图将数据集中的样本划分为若干个不相交的子集,我们称之为“簇”(cluster)。本章我们将深入探讨三种最具代表性的聚类算法:K-均值(K-Means)、层次聚类(Hierarchical
- 结构型智能科技的关键可行性——信息型智能向结构型智能的转变(修改提纲)
刘海东刘海东
人工智能机器学习算法
结构型智能科技的关键可行性——信息型智能向结构型智能的转变1.信息型智能科技概述1.1传统计算机科技的信息型继承者1.2信息型智能环境1.3信息型智能主体1.4机器学习创造的智能1.5信息型智能科技的缺陷2.结构型智能科技概述2.1传统计算机科技向生命结构的发展2.2结构型智能科技的环境2.3结构型智能科技创造的机器生命2.4结构型智能科技的科学性3.结构型智能科技的关键可行性——信息型智能向结构
- 多模态大模型:技术原理与实战 看清GPT的进化史和创新点
AI天才研究院
AgenticAI实战计算AI人工智能与大数据计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
多模态大模型:技术原理与实战看清GPT的进化史和创新点1.背景介绍1.1人工智能的发展历程1.1.1早期人工智能1.1.2机器学习时代1.1.3深度学习的崛起1.2自然语言处理的演进1.2.1基于规则的方法1.2.2统计机器学习方法1.2.3深度学习方法1.3大语言模型的出现1.3.1Transformer架构的提出1.3.2GPT系列模型的发展1.3.3多模态大模型的兴起2.核心概念与联系2.1
- 【机器学习|学习笔记】组合特征(Feature Combinations)是提升模型性能、挖掘特征交互信息、增强非线性表达能力的有效手段。
努力毕业的小土博^_^
机器学习学习笔记机器学习学习笔记人工智能神经网络深度学习
【机器学习|学习笔记】组合特征(FeatureCombinations)是提升模型性能、挖掘特征交互信息、增强非线性表达能力的有效手段。【机器学习|学习笔记】组合特征(FeatureCombinations)是提升模型性能、挖掘特征交互信息、增强非线性表达能力的有效手段。文章目录【机器学习|学习笔记】组合特征(FeatureCombinations)是提升模型性能、挖掘特征交互信息、增强非线性表达
- R语言的软件开发工具
纪霁然
包罗万象golang开发语言后端
R语言的软件开发工具引言R语言因其强大的数据分析能力和丰富的统计包,自发布以来便广受欢迎。随着数据科学和分析的迅猛发展,R语言也逐渐成为数据分析、机器学习和统计建模领域的重要工具。为了更好地利用R语言进行软件开发,许多软件开发工具和环境应运而生。本文将深入探讨R语言的主要开发工具,帮助开发者更高效地进行数据处理和分析。1.R和RStudio基础R语言本身是一个用于统计计算和图形绘制的编程语言,而R
- 结合创新idea:机器学习+运筹优化=CCF高端局
Ai多利
机器学习人工智能
2024深度学习发论文&模型涨点之——机器学习+运筹优化机器学习是人工智能的一个分支,它使计算机系统能够从数据中学习并改进其性能,而无需进行明确的编程。运筹优化,也称为运筹学或运营管理,是应用数学的一个分支,它使用数学模型和算法来支持复杂决策过程的制定。机器学习与运筹优化的结合是一个前沿且活跃的研究领域,它们相互补充,为解决复杂问题提供了新的思路和方法。小编整理了一些机器学习+运筹优化【论文+代码
- Jupyter安装指南及Python配置
CodeWG
pythonjupyteridePython
Jupyter是一个非常流行的交互式计算环境,广泛用于数据分析、机器学习和科学计算等领域。本文将详细介绍如何安装Jupyter并配置Python环境。步骤1:安装Python首先,我们需要安装Python。请按照以下步骤进行操作:打开Python官方网站(https://www.python.org)并下载适用于您操作系统的最新版本的Python。运行下载的安装程序,并按照向导的指示进行安装。在安
- 矩阵求逆(JAVA)利用伴随矩阵
qiuwanchi
利用伴随矩阵求逆矩阵
package gaodai.matrix;
import gaodai.determinant.DeterminantCalculation;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
/**
* 矩阵求逆(利用伴随矩阵)
* @author 邱万迟
- 单例(Singleton)模式
aoyouzi
单例模式Singleton
3.1 概述 如果要保证系统里一个类最多只能存在一个实例时,我们就需要单例模式。这种情况在我们应用中经常碰到,例如缓存池,数据库连接池,线程池,一些应用服务实例等。在多线程环境中,为了保证实例的唯一性其实并不简单,这章将和读者一起探讨如何实现单例模式。 3.2
- [开源与自主研发]就算可以轻易获得外部技术支持,自己也必须研发
comsci
开源
现在国内有大量的信息技术产品,都是通过盗版,免费下载,开源,附送等方式从国外的开发者那里获得的。。。。。。
虽然这种情况带来了国内信息产业的短暂繁荣,也促进了电子商务和互联网产业的快速发展,但是实际上,我们应该清醒的看到,这些产业的核心力量是被国外的
- 页面有两个frame,怎样点击一个的链接改变另一个的内容
Array_06
UIXHTML
<a src="地址" targets="这里写你要操作的Frame的名字" />搜索
然后你点击连接以后你的新页面就会显示在你设置的Frame名字的框那里
targerts="",就是你要填写目标的显示页面位置
=====================
例如:
<frame src=&
- Struts2实现单个/多个文件上传和下载
oloz
文件上传struts
struts2单文件上传:
步骤01:jsp页面
<!--在进行文件上传时,表单提交方式一定要是post的方式,因为文件上传时二进制文件可能会很大,还有就是enctype属性,这个属性一定要写成multipart/form-data,不然就会以二进制文本上传到服务器端-->
<form action="fileUplo
- 推荐10个在线logo设计网站
362217990
logo
在线设计Logo网站。
1、http://flickr.nosv.org(这个太简单)
2、http://www.logomaker.com/?source=1.5770.1
3、http://www.simwebsol.com/ImageTool
4、http://www.logogenerator.com/logo.php?nal=1&tpl_catlist[]=2
5、ht
- jsp上传文件
香水浓
jspfileupload
1. jsp上传
Notice:
1. form表单 method 属性必须设置为 POST 方法 ,不能使用 GET 方法
2. form表单 enctype 属性需要设置为 multipart/form-data
3. form表单 action 属性需要设置为提交到后台处理文件上传的jsp文件地址或者servlet地址。例如 uploadFile.jsp 程序文件用来处理上传的文
- 我的架构经验系列文章 - 前端架构
agevs
JavaScriptWeb框架UIjQuer
框架层面:近几年前端发展很快,前端之所以叫前端因为前端是已经可以独立成为一种职业了,js也不再是十年前的玩具了,以前富客户端RIA的应用可能会用flash/flex或是silverlight,现在可以使用js来完成大部分的功能,因此js作为一门前端的支撑语言也不仅仅是进行的简单的编码,越来越多框架性的东西出现了。越来越多的开发模式转变为后端只是吐json的数据源,而前端做所有UI的事情。MVCMV
- android ksoap2 中把XML(DataSet) 当做参数传递
aijuans
android
我的android app中需要发送webservice ,于是我使用了 ksop2 进行发送,在测试过程中不是很顺利,不能正常工作.我的web service 请求格式如下
[html]
view plain
copy
<Envelope xmlns="http://schemas.
- 使用Spring进行统一日志管理 + 统一异常管理
baalwolf
spring
统一日志和异常管理配置好后,SSH项目中,代码以往散落的log.info() 和 try..catch..finally 再也不见踪影!
统一日志异常实现类:
[java]
view plain
copy
package com.pilelot.web.util;
impor
- Android SDK 国内镜像
BigBird2012
android sdk
一、镜像地址:
1、东软信息学院的 Android SDK 镜像,比配置代理下载快多了。
配置地址, http://mirrors.neusoft.edu.cn/configurations.we#android
2、北京化工大学的:
IPV4:ubuntu.buct.edu.cn
IPV4:ubuntu.buct.cn
IPV6:ubuntu.buct6.edu.cn
- HTML无害化和Sanitize模块
bijian1013
JavaScriptAngularJSLinkySanitize
一.ng-bind-html、ng-bind-html-unsafe
AngularJS非常注重安全方面的问题,它会尽一切可能把大多数攻击手段最小化。其中一个攻击手段是向你的web页面里注入不安全的HTML,然后利用它触发跨站攻击或者注入攻击。
考虑这样一个例子,假设我们有一个变量存
- [Maven学习笔记二]Maven命令
bit1129
maven
mvn compile
compile编译命令将src/main/java和src/main/resources中的代码和配置文件编译到target/classes中,不会对src/test/java中的测试类进行编译
MVN编译使用
maven-resources-plugin:2.6:resources
maven-compiler-plugin:2.5.1:compile
&nbs
- 【Java命令二】jhat
bit1129
Java命令
jhat用于分析使用jmap dump的文件,,可以将堆中的对象以html的形式显示出来,包括对象的数量,大小等等,并支持对象查询语言。 jhat默认开启监听端口7000的HTTP服务,jhat是Java Heap Analysis Tool的缩写
1. 用法:
[hadoop@hadoop bin]$ jhat -help
Usage: jhat [-stack <bool&g
- JBoss 5.1.0 GA:Error installing to Instantiated: name=AttachmentStore state=Desc
ronin47
进到类似目录 server/default/conf/bootstrap,打开文件 profile.xml找到: Xml代码<bean
name="AttachmentStore"
class="org.jboss.system.server.profileservice.repository.AbstractAtta
- 写给初学者的6条网页设计安全配色指南
brotherlamp
UIui自学ui视频ui教程ui资料
网页设计中最基本的原则之一是,不管你花多长时间创造一个华丽的设计,其最终的角色都是这场秀中真正的明星——内容的衬托
我仍然清楚地记得我最早的一次美术课,那时我还是一个小小的、对凡事都充满渴望的孩子,我摆放出一大堆漂亮的彩色颜料。我仍然记得当我第一次看到原色与另一种颜色混合变成第二种颜色时的那种兴奋,并且我想,既然两种颜色能创造出一种全新的美丽色彩,那所有颜色
- 有一个数组,每次从中间随机取一个,然后放回去,当所有的元素都被取过,返回总共的取的次数。写一个函数实现。复杂度是什么。
bylijinnan
java算法面试
import java.util.Random;
import java.util.Set;
import java.util.TreeSet;
/**
* http://weibo.com/1915548291/z7HtOF4sx
* #面试题#有一个数组,每次从中间随机取一个,然后放回去,当所有的元素都被取过,返回总共的取的次数。
* 写一个函数实现。复杂度是什么
- struts2获得request、session、application方式
chiangfai
application
1、与Servlet API解耦的访问方式。
a.Struts2对HttpServletRequest、HttpSession、ServletContext进行了封装,构造了三个Map对象来替代这三种对象要获取这三个Map对象,使用ActionContext类。
----->
package pro.action;
import java.util.Map;
imp
- 改变python的默认语言设置
chenchao051
python
import sys
sys.getdefaultencoding()
可以测试出默认语言,要改变的话,需要在python lib的site-packages文件夹下新建:
sitecustomize.py, 这个文件比较特殊,会在python启动时来加载,所以就可以在里面写上:
import sys
sys.setdefaultencoding('utf-8')
&n
- mysql导入数据load data infile用法
daizj
mysql导入数据
我们常常导入数据!mysql有一个高效导入方法,那就是load data infile 下面来看案例说明
基本语法:
load data [low_priority] [local] infile 'file_name txt' [replace | ignore]
into table tbl_name
[fields
[terminated by't']
[OPTI
- phpexcel导入excel表到数据库简单入门示例
dcj3sjt126com
PHPExcel
跟导出相对应的,同一个数据表,也是将phpexcel类放在class目录下,将Excel表格中的内容读取出来放到数据库中
<?php
error_reporting(E_ALL);
set_time_limit(0);
?>
<html>
<head>
<meta http-equiv="Content-Type"
- 22岁到72岁的男人对女人的要求
dcj3sjt126com
22岁男人对女人的要求是:一,美丽,二,性感,三,有份具品味的职业,四,极有耐性,善解人意,五,该聪明的时候聪明,六,作小鸟依人状时尽量自然,七,怎样穿都好看,八,懂得适当地撒娇,九,虽作惊喜反应,但看起来自然,十,上了床就是个无条件荡妇。 32岁的男人对女人的要求,略作修定,是:一,入得厨房,进得睡房,二,不必服侍皇太后,三,不介意浪漫蜡烛配盒饭,四,听多过说,五,不再傻笑,六,懂得独
- Spring和HIbernate对DDM设计的支持
e200702084
DAO设计模式springHibernate领域模型
A:数据访问对象
DAO和资源库在领域驱动设计中都很重要。DAO是关系型数据库和应用之间的契约。它封装了Web应用中的数据库CRUD操作细节。另一方面,资源库是一个独立的抽象,它与DAO进行交互,并提供到领域模型的“业务接口”。
资源库使用领域的通用语言,处理所有必要的DAO,并使用领域理解的语言提供对领域模型的数据访问服务。
- NoSql 数据库的特性比较
geeksun
NoSQL
Redis 是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库,并提供多种语言的API。目前由VMware主持开发工作。
1. 数据模型
作为Key-value型数据库,Redis也提供了键(Key)和值(Value)的映射关系。除了常规的数值或字符串,Redis的键值还可以是以下形式之一:
Lists (列表)
Sets
- 使用 Nginx Upload Module 实现上传文件功能
hongtoushizi
nginx
转载自: http://www.tuicool.com/wx/aUrAzm
普通网站在实现文件上传功能的时候,一般是使用Python,Java等后端程序实现,比较麻烦。Nginx有一个Upload模块,可以非常简单的实现文件上传功能。此模块的原理是先把用户上传的文件保存到临时文件,然后在交由后台页面处理,并且把文件的原名,上传后的名称,文件类型,文件大小set到页面。下
- spring-boot-web-ui及thymeleaf基本使用
jishiweili
springthymeleaf
视图控制层代码demo如下:
@Controller
@RequestMapping("/")
public class MessageController {
private final MessageRepository messageRepository;
@Autowired
public MessageController(Mes
- 数据源架构模式之活动记录
home198979
PHP架构活动记录数据映射
hello!架构
一、概念
活动记录(Active Record):一个对象,它包装数据库表或视图中某一行,封装数据库访问,并在这些数据上增加了领域逻辑。
对象既有数据又有行为。活动记录使用直截了当的方法,把数据访问逻辑置于领域对象中。
二、实现简单活动记录
活动记录在php许多框架中都有应用,如cakephp。
<?php
/**
* 行数据入口类
*
- Linux Shell脚本之自动修改IP
pda158
linuxcentosDebian脚本
作为一名
Linux SA,日常运维中很多地方都会用到脚本,而服务器的ip一般采用静态ip或者MAC绑定,当然后者比较操作起来相对繁琐,而前者我们可以设置主机名、ip信息、网关等配置。修改成特定的主机名在维护和管理方面也比较方便。如下脚本用途为:修改ip和主机名等相关信息,可以根据实际需求修改,举一反三!
#!/bin/sh
#auto Change ip netmask ga
- 开发环境搭建
独浮云
eclipsejdktomcat
最近在开发过程中,经常出现MyEclipse内存溢出等错误,需要重启的情况,好麻烦。对于一般的JAVA+TOMCAT项目开发,其实没有必要使用重量级的MyEclipse,使用eclipse就足够了。尤其是开发机器硬件配置一般的人。
&n
- 操作日期和时间的工具类
vipbooks
工具类
大家好啊,好久没有来这里发文章了,今天来逛逛,分享一篇刚写不久的操作日期和时间的工具类,希望对大家有所帮助。
/*
* @(#)DataFormatUtils.java 2010-10-10
*
* Copyright 2010 BianJing,All rights reserved.
*/
package test;
impor