垃圾小白羊leetcode刷题记录1
def twoSum(self, nums: List[int], target: int) -> List[int]:
for i, num in enumerate(nums):
for j in range(i+1,len(nums)):
if nums[j] == target-num:
return [i,j]
两层循环,时间复杂度O(n2)
大佬解法:
def twoSum(self, nums: List[int], target: int) -> List[int]:
num_dict = {
}
for i, num in enumerate(nums):
if num_dict.get(target - num) is not None:
return [num_dict.get(target - num), i]
num_dict[num] = i
利用hash表,以空间换时间,只需一层循环,时间复杂度O(n)。
我的解法:
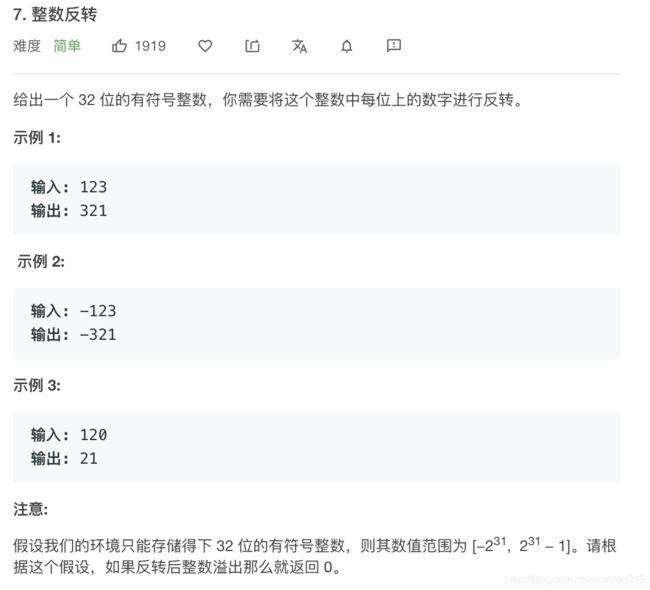
def reverse(self, x: int) -> int:
a = []
x_inversed = 0
signx = 1
if x < 0:
signx = -1
x = -x
if x == 0:
return 0
while x != 0:
a.append(x%10)
x = x//10
for i in range(len(a)):
x_inversed += a[len(a)-i-1]*(10**i)
if (x_inversed <= 2**31-1) & (x_inversed >= -2**31):
return x_inversed * signx
else:
return 0
特别处理x为负和零的情况,通过整除的方式获得各位数字,倒转后组合为反转后的数字。两次循环,时间复杂度O(2n)。
大佬解法:
def reverse(self, x: int) -> int:
x_inversed = 0
signx = 1
if x < 0:
signx = -1
x = -x
while x != 0:
x_inversed = x_inversed*10 + (x%10)
x = x//10
if (x_inversed <= 2**31-1) & (x_inversed >= -2**31):
return x_inversed * signx
else:
return 0
思路一致,算法更加优化简练,不需单独处理x为0的特殊情况,仅需一次循环,时间复杂度O(n)。
我的解法:
def isPalindrome(self, x: int) -> bool:
if x < 0:
return False
inversed = 0
x1 = x
while x1 !=0:
inversed = inversed*10 + (x1%10)
x1 = x1//10
return x == inversed
单独考虑x小于0的情况,与前一题思路相似。
大佬解法:
class Solution:
def isPalindrome(self, x: int) -> bool:
xlist = list(str(x))
l, r = 0, len(xlist)-1
while r > l:
if xlist[l] != xlist[r]:
return False
l += 1
r -= 1
return True
将数字转为字符列表,采用首位双指针的方式比对。
我的解法:
class Solution:
def romanToInt(self, s: str) -> int:
d = {
'I':1, 'V':5, 'X':10, 'L':50, 'C':100, 'D':500, 'M':1000}
n = 0
for i in range(len(s)-1):
if d[s[i]] < d[s[i+1]]:
n -= d[s[i]]
else:
n += d[s[i]]
n += d[s[-1]]
return n
若某位对应数字大于后一位,则减去该位,否则加上该位。
我的解法:
class Solution:
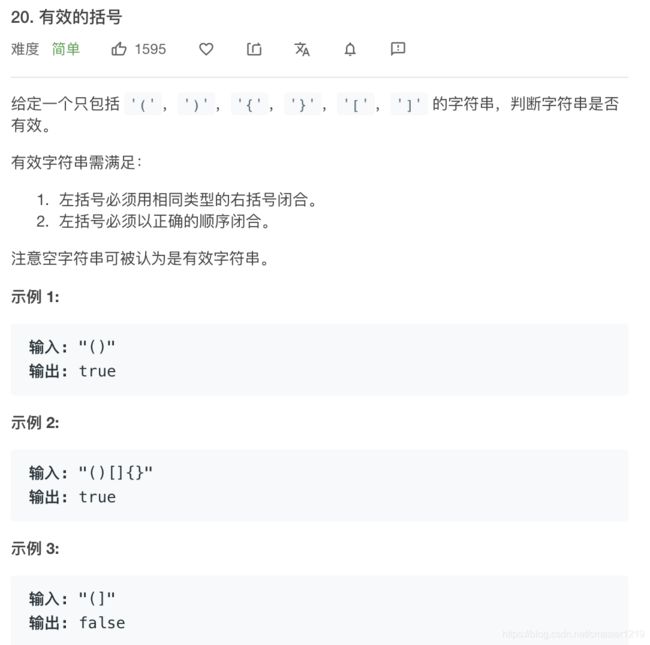
def isValid(self, s: str) -> bool:
b = {
'(':')', '{':'}', '[':']'}
stack = ['base']
s_list = list(s)
for i in range(len(s_list)):
if s_list[i] in b.keys():
stack.append(b[s_list[i]])
else:
if s_list[i] != stack.pop():
return False
return len(stack) == 1
遍历括号集,若出现某种左括号则把对应右括号压入栈;若出现右括号,弹出栈内第一个值,若不一致直接输出False。栈内初始设置一元素’base’,用以处理括号集第一个元素为右括号情况。遍历结束后判断栈内是否只剩下’base’,若是返回True。
优化:开头添加判断括号集长度是否为奇数,若是直接返回False。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
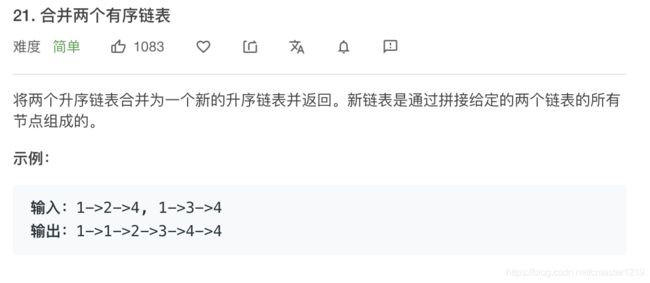
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
if l1 is None:
return l2
elif l2 is None:
return l1
else:
l = ListNode()
header = l
while 1:
if l1.val <= l2.val:
l.next = l1
l = l.next
l1 = l1.next
else:
l.next = l2
l = l.next
l2 = l2.next
if l1 is None:
l.next = l2
break
if l2 is None:
l.next = l1
break
return header.next
首先特殊考虑l1或l2一者为空的情况。创建新链表l,遍历比对l1和l2数值大小,若其中一个链表遍历完成,则将另一链表的剩余部分直接附在结尾,结束循环。
大佬解法:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
if not l1:
return l2
if not l2:
return l1
if l1.val <= l2.val:
l1.next = self.mergeTwoLists(l1.next, l2)
return l1
else:
l2.next = self.mergeTwoLists(l1, l2.next)
return l2
递归算法,相当于每次递归添加首元素较小链表的首元素,剩下部分与另一链表一起继续递归。
我的解法:
class Solution:
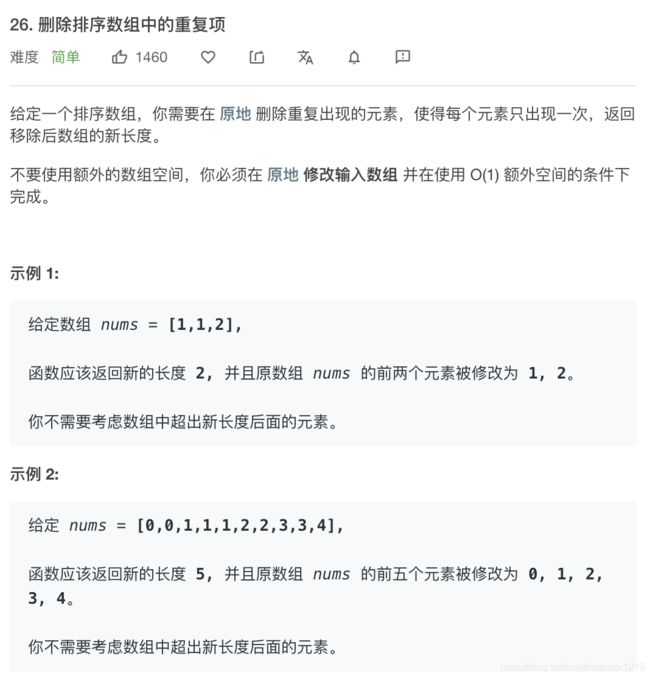
def removeDuplicates(self, nums: List[int]) -> int:
if not nums:
return None
j = 1
origin = nums[0]
for i in range(1, len(nums)):
if nums[i] != origin:
nums[j] = nums[i]
origin = nums[i]
j += 1
return j
由于数组是排序的,记录当前的数字,遍历数组,若出现与当前不同的数字,则将表头相应位置赋值为该数字,当前数字更新,继续遍历。
大佬解法:
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
pre,cur=0,1
while cur<len(nums):
if nums[pre]==nums[cur]:
nums.pop(cur)
else:
pre,cur=pre+1,cur+1
return len(nums)
用两个指针,指向第一个和第二个元素,如果他们相等,删除第二个元素。指针还指向原来的位置,继续比较。不等的话,两个指针位置都加一。遍历结束即可。
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
j = len(nums)-1
for i in range(len(nums)-1,-1,-1):
if nums[i] == val:
nums[j], nums[i] = nums[i], nums[j]
j -= 1
return j+1
与前一题思路类似,将目标值全部置换到列表尾部。时间复杂度为O(n),强于直接使用remove的方法(O(n)2)。
我的解法:
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
ln = len(needle)
lh = len(haystack)
i = 0
j = 0
t = -1
while i <= lh - ln:
while j < ln:
if haystack[i] != needle[j]:
if t < 0:
i += 1
else:
i = t
t = -1
j = 0
break
else:
j += 1
i += 1
if i == lh: break
if ((haystack[i] == needle[0]) & (j > 0) & (t < 0)):
t = i
if j == ln:
return i - ln
return -1
略微改进的暴力遍历,如果首字母一直匹配不对,则退化为暴力遍历。若前若干字符匹配正确,needle第j个字符匹配失败且hatstack匹配正确的前j个字符中未出现needle首字符,则直接跳过当前匹配所有字符,从i+1处开始继续匹配。若出现过needle首字符,则i变更为其出现的第一个位置t。
大佬解法
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
ln = len(needle)
lh = len(haystack)
def calshift(s):
shift = {
}
for i in range(ln-1, -1, -1):
if not shift.get(needle[i]):
shift[needle[i]] = ln - i
return shift[s] if shift.get(s) else ln+1
if (not haystack) & (not needle):
return 0
if not haystack:
return -1
i = 0
while i <= lh - ln:
if haystack[i:i+ln] != needle:
if i == lh - ln:
return -1
else:
i = i + calshift(haystack[i+ln])
else:
return i
return -1
使用偏移表,根据匹配字段后一位字符判断指针偏移的位数,当字符重复性不强时,可以大大提高匹配效率。

我的解法:
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
n = len(nums)
if target <= nums[0]:
return 0
elif target > nums[-1]:
return n
else:
l = 0
r = n-1
while r-l > 1:
i = (l+r)//2
if target >= nums[i]:
l = i
else:
r = i
return l if target <= nums[l] else l+1
特殊处理添加到头尾情况后,采用二分法查找。