垃圾小白羊的leetcode刷题记录6
我的解法:
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
if not matrix:
return []
if len(matrix)==1:
return matrix[0]
m,n = len(matrix),len(matrix[0])
directions = [(0,1),(0,-1),(1,0),(-1,0)] # right, left, down, up
top, bottom, left, right = 1, m-1, 0, n-1
ans, count = [], 0
i, j, cur_d = 0, 0, directions[0]
while count < m*n:
ans.append(matrix[i][j])
count += 1
if (j == right) and (cur_d == directions[0]):
cur_d = directions[2]
right -= 1
elif i == bottom and cur_d == directions[2]:
cur_d = directions[1]
bottom -= 1
elif j == left and cur_d == directions[1]:
cur_d = directions[3]
left += 1
elif i == top and cur_d == directions[3]:
cur_d = directions[0]
top += 1
m_i, m_j = cur_d
i, j = i+m_i, j+m_j
return ans
定义四个移动方向和四个边界,当移动方向与某边界相互垂直时,需要按照顺指针方向变换到下一方向,同时调整新的边界。该算法比较不完美的地方在于需要把初始上边界设置为第二行,因此需要特殊考虑只有一行的矩阵,可以像官方题解一样,用一个m*n的矩阵记录各个元素被调用情况,这样可以不用记录更新各边界。实际上各个方向是按特定顺序变化的,因此将储存四个方向的列表顺序调整为顺时针方向将会方便方向选取。
大佬解法:
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
if not matrix or not matrix[0]:
return list()
rows, columns = len(matrix), len(matrix[0])
order = list()
left, right, top, bottom = 0, columns - 1, 0, rows - 1
while left <= right and top <= bottom:
for column in range(left, right + 1):
order.append(matrix[top][column])
for row in range(top + 1, bottom + 1):
order.append(matrix[row][right])
if left < right and top < bottom:
for column in range(right - 1, left, -1):
order.append(matrix[bottom][column])
for row in range(bottom, top, -1):
order.append(matrix[row][left])
left, right, top, bottom = left + 1, right - 1, top + 1, bottom - 1
return order
按照从内到外逐层遍历,首先将当前层左上角定于(0,0),右下角定于(m-1,n-1),依次遍历外圈元素,一圈遍历完成后,左上角横纵坐标加一,右下角横纵坐标减一,继续遍历。
我的解法:
class Solution:
def canJump(self, nums: List[int]) -> bool:
n = len(nums)
pl, pr = 0, 0
ran = 0
while 1:
for i in range(pl,pr+1):
if ran < i+nums[i]:
ran = i+nums[i]
if ran >= n-1:
return True
if ran <= pr:
return Falsen
pl, pr = pr+1, ran
如果使用暴力解法,我们需要查找所有可能,会出现很多重复,时间复杂度为O(n2)。另一种想法是我们设法找到每一步的查找范围,使得不同步查找范围间没有交集。具体方法如下:对于前一个查找范围[pl, pr],我们找到该范围能跳到的最远位置ran。如果ran>n-1,则可以跳到终点;如果ran<=pr,则说明不会有新的搜索范围产生,无法到达终点;除这两种情况外,更新搜索区间为[pr+1, ran],继续搜索。整体相当于遍历列表一遍,时间复杂度O(n)。
大佬解法:
class Solution:
def canJump(self, nums: List[int]) -> bool:
n, rightmost = len(nums), 0
for i in range(n):
if i <= rightmost:
rightmost = max(rightmost, i + nums[i])
if rightmost >= n - 1:
return True
return False
相同的思路,但是只需要单指针。
我的解法:
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
n = len(intervals)
if n <= 1:
return intervals
intervals = sorted(intervals, key=lambda x: x[0])
ans = []
cur_inte = intervals[0]
for i in range(1, n):
new_inte = intervals[i]
if new_inte[0] > cur_inte[1]:
ans.append(cur_inte)
cur_inte=new_inte
continue
if new_inte[1] >= cur_inte[1]:
cur_inte[1] = new_inte[1]
ans.append(cur_inte)
return ans
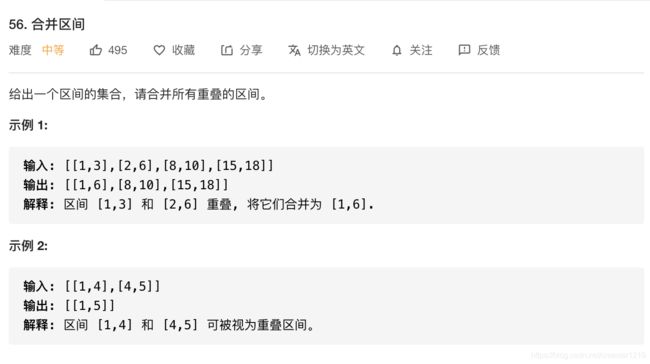
首先将区间列表按照左边界由小到大排序,此后我们首先将第一个区间作为工作区间,由其后一个区间开始判断两区间是否有重合,如果后一区间的左边界大于工作区间的右边界,则两区间无交集,将工作区间加入结果集,同时将工作区间更新为后一区间;如果两区间有交集,若后一区间的右边界大于工作区间的右边界,则更新工作区间的右边界。依次遍历区间列表至结束,再将最后一个工作区间加入结果集即可。时间复杂度主要来自于排序O(nlogn),空间复杂度为结果列表O(n)。
我的解法:
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
matrix = [[0]*n for i in range(n)]
tl = [0,0]
br = [n-1, n-1]
num = 1
while num<=n*n:
for i in range(tl[1], br[1]+1):
matrix[tl[0]][i] = num
num += 1
for i in range(tl[0]+1, br[0]+1):
matrix[i][br[1]] = num
num += 1
for i in range(br[1]-1, tl[1]-1, -1):
matrix[br[0]][i] = num
num += 1
for i in range(br[0]-1, tl[0], -1):
matrix[i][tl[1]] = num
num += 1
tl[0], tl[1] = tl[0]+1, tl[1]+1
br[0], br[1] = br[0]-1, br[0]-1
return matrix
按层顺时针输入数字,由top-left点和bottom-right点确定层的范围,输入顺序为(top, left)->(top, right), (top+1, right)->(bottom, right), (bottom, right-1)->(bottom, left), (bottom+1,left)->(top-1, left)。一层输入完成后,将top-left点和bottom-right点向内移动一层,即可继续进行内圈输入,当输入数字总数等于n*n时输出结果矩阵。
我的解法:
class Solution:
def getPermutation(self, n: int, k: int) -> str:
def divisor(n):
d = 1
while n>1:
d = d*n
n -= 1
return d
ans, nums = '', list(range(1,n+1))
k -= 1
while nums:
d = divisor(n-1)
index = k//d
ans = ans + str(nums[index])
k = k - index*d
n -= 1
nums.remove(nums[index])
return ans
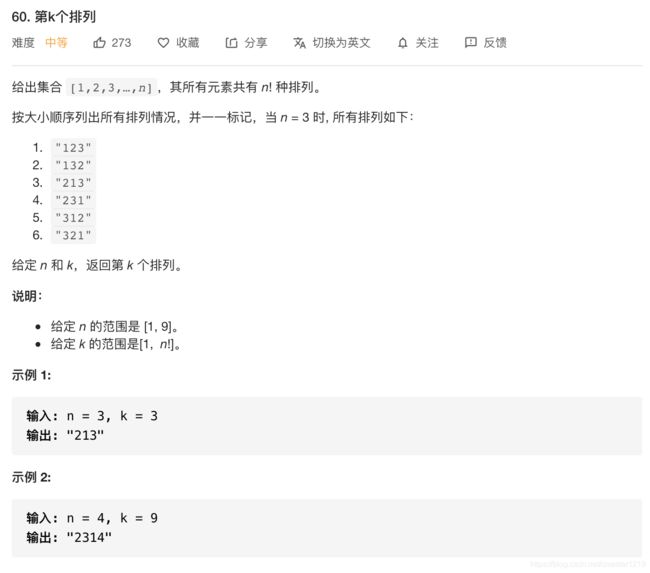
首先n个数会有n!个排列,由n个(n-1)!排列组成,因此我们可以通过判断第k个排列属于哪一个(n-1)!排列来由左向右地确定k排列的各位数字。需要注意的是第k个排列对应索引为k-1,因此需重新定义k=k-1。定义一个函数来计算(n-1)!的大小,用于作为k的除数,确定k排列从右向左第n个数字。定义一个1到n的列表nums来记录剩下的数字,当nums为空时即已找到了对应排列。时间复杂度为删除列表元素造成的O(n2),空间复杂度为存放1到n列表所用的O(n)。
我的解法:
class Solution:
def rotateRight(self, head: ListNode, k: int) -> ListNode:
if not head:
return
count = 1
cur1 = head
while cur1.next:
count += 1
cur1 = cur1.next
cur1.next = head
new_head_index = count-k%count
if new_head_index==0:
return head
cur2 = head
for i in range(new_head_index-1):
cur2 = cur2.next
head = cur2.next
cur2.next = None
return head
主要思路为两部分,首先遍历一遍链表,得到链表的长度n,同时将链表头尾相连。计算新链表头节点位置n-k%n,将指针移动至新链表头节点的前一个节点,将该节点的下一个节点也就是新头节点设为头节点,并把该节点指向None,即完成了旋转。
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
up = [[0]*m for _ in range(n)]
for i in range(n):
for j in range(m):
if i == 0 and j == 0:
up[i][j] = 1
elif j == 0:
up[i][j] = up[i-1][j]
elif i == 0:
up[i][j] = up[i][j-1]
else:
up[i][j] = up[i-1][j]+up[i][j-1]
return up[n-1][m-1]
经典动态规划算法。我们将状态定为up[i, j],它表示从起点出发到达第i行第j列位置的可能路径数量。由于只能向下或向右移动,我们可以构建起关系式为up[i, j] = up[i-1, j]+up[i, j-1],同时要考虑到左侧和上侧边界条件,左侧边界的位置只能由其上侧位置抵达,上侧边界的位置只能由其左侧位置抵达。我们构建一个mxn的矩阵用来存放和计算结果,观察关系式的特点可以发现要计算一个位置的可能情况,需要其上侧和左侧位置的取值,因此我们按照行优先的方式从头到尾遍历计算一次矩阵即可。时间复杂度O(MN)。
我的解法:
class Solution:
def simplifyPath(self, path: str) -> str:
path_stack, n = [], len(path)
cur, i = '', 0
while i<n:
if path[i] == '/':
i += 1
else:
while i<n and path[i] != '/' :
cur += path[i]
i += 1
if cur == '..' and path_stack:
path_stack.pop()
elif cur != '..' and cur != '.':
path_stack.append(cur)
cur = ''
return '/'+'/'.join(path_stack)
’ / ‘和’ . ‘没有特别含义,因此我们重点关注’ . . ‘和其他字符。我们构架一个栈来储存目录名,从头开始遍历原路径,若遍历到非‘ / ’字符,开始记录该字符串直至遍历到‘ / ’结束,如果该字符串为目录名则压入栈,如果是’ . . '且栈中存有元素,则弹出栈顶元素,其他情况均不做操作。将记录的字符串初始化,继续遍历。遍历完成后,将栈中元素用‘ / ’分隔后输出即可。
class Solution:
def setZeroes(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
m, n = len(matrix), len(matrix[0])
first_row, first_column = False, False
for i in range(n):
if matrix[0][i]==0:
first_row = True
break
for i in range(m):
if matrix[i][0]==0:
first_column = True
break
for i in range(1,m):
for j in range(1,n):
if matrix[i][j] == 0:
matrix[0][j] = 0
matrix[i][0] = 0
for i in range(1,m):
if matrix[i][0] == 0:
matrix[i] = [0]*n
for j in range(1,n):
if matrix[0][j] == 0:
for k in range(m):
matrix[k][j] = 0
if first_row:
matrix[0] = [0]*n
if first_column:
for k in range(m):
matrix[k][0] = 0
该题的难点在于如何只利用O(1)的空间复杂度解决问题,我们考虑用第一行和第一列来记录该行或列是否需要置零,若需要,我们把第一行或列的对应元素置零。我们首先要判断第一行或第一列中是否本身有零,以此判断第一行或列是否需要置零,遍历第一行和第一列,用两个bool变量来记录是否需要置零。从第二行第二列元素开始遍历剩余的矩阵,如果遇到零则将对应行和列的第一个元素置零。遍历结束后,将第一行元素为0的列置零,第一列元素为0的行置零。整个过程遍历矩阵两次,时间复杂度O(MxN),空间复杂度O(1)。
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
if not matrix or not matrix[0]:
return False
if matrix[0][0] > target or matrix[-1][-1]< target:
return False
row_index = 0
first_col = [x[0] for x in matrix]
c_l, c_r = 0, len(first_col)-1
while c_r-c_l>1:
c_mid = (c_l+c_r)//2
if first_col[c_mid] < target:
c_l = c_mid
elif first_col[c_mid] > target:
c_r = c_mid
else:
return True
if matrix[c_l][-1] >= target:
row_index = c_l
else:
row_index = c_r
row = matrix[row_index]
r_l, r_r = 0, len(row)-1
while r_l<=r_r:
r_mid = (r_l+r_r+1)//2
if row[r_mid] < target:
r_l = r_mid+1
elif row[r_mid] > target:
r_r = r_mid-1
else:
return True
return False
官方解法是利用索引变换将矩阵二分搜索变为列表二分搜索,时间复杂度为O(log(mn))。而我的方法使用两次二分搜索,似乎更复杂一些。
具体思路为:首先确定target在矩阵范围内,若不在直接返回false。将矩阵每行第一个元素拿出来组成一个列表,我们希望首先通过一次二分查找缩小target所在行的范围。由于每行有多个元素,我们只能将范围缩减到两行内。这时我们比较target与两行中行1最后一个元素大小,若小于或等于则确定target位于行1中,否则位于行1中,否则位于行2中,此时再在最终确定的行中二分搜索target。时间复杂度O(log(mn))。
我的解法:
class Solution:
def sortColors(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
n = len(nums)
p0, p2 = 0, n-1
while p0<n and nums[p0]==0: p0 += 1
while p2>=0 and nums[p2]==2: p2 -= 1
p = p0
while p <= p2:
if nums[p] == 0:
nums[p], nums[p0] = nums[p0], nums[p]
p0 += 1
p += 1
elif nums[p] == 1:
p += 1
elif nums[p] == 2:
nums[p], nums[p2] = nums[p2], nums[p]
p2 -= 1
双指针法,严格来说为三指针法。首先从前往后遍历数组找到第一个不为0的元素定义指针p0,从后往前遍历找到第一个不为2的元素定义p2,用第三个指针p从p0开始向p2方向遍历,若遍历到1则跳过继续遍历,若遍历到0则与p0对应元素互换。这里需要注意,因为p左边的元素全部遍历过,所以我们可以确定换到p指针处的元素一定为1,因此可以把p向右移动一格。若遍历到2,则与p2对应的元素互换,由于没有遍历过从p2换过来的元素,因此指针p不能移动,需要再次判别指针p处的元素。时间复杂度O(n),空间复杂度O(1)。
我的解法:
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
def backtrack(first=1, curr=[]):
if len(curr) == k:
ans.append(curr[:])
return
for i in range(first, n+1):
curr.append(i)
backtrack(i+1, curr)
curr.pop()
ans = []
backtrack()
return ans
典型回溯算法,定义回溯函数,参数为起始数字以及现有组合集合,通过循环遍历将从剩余元素中依次挑选一个元素添加到现有集合中,再在递归后将添加的元素删除以完成回溯,当组合集合元素个数达到k时,将组合加入结果集中。时间复杂度O( k C N k kC_N^k kCNk)。
我的解法:
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
if not nums:
return 0
p, pt, n = 0, 0, len(nums)
last, count = nums[0], 0
while p < n:
if nums[p] == last:
count += 1
else:
count = 1
if count <= 2:
nums[pt] = nums[p]
pt += 1
last = nums[p]
p += 1
return pt
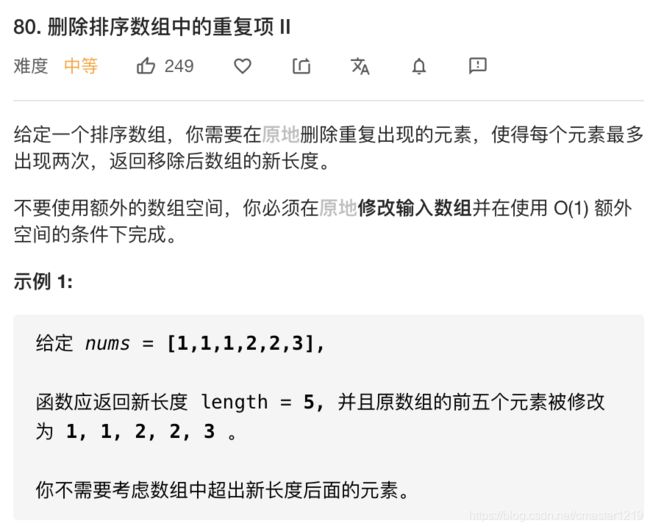
双指针法,一个指针p用来遍历列表,另一个指针pt用来更新符合条件的元素。遍历列表,记录上一个元素last和当前相同元素计数count,若遍历到的元素与上个元素相同,计数count加一,否则count重置为1;若计数count大于2,只有当count小于等于2时,才能将指针p对应的元素更新到pt处,否则不更新pt,只继续遍历列表。时间复杂度O(n),空间复杂度O(1)。
我的解法:
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
def search_around(i0, j0, t, used):
if t<n-1 and board[i0][j0] == word[t]:
t += 1
possible = []
used[i0][j0] = True
for i, j in zip([-1,0,1,0],[0,1,0,-1]):
i1, j1 = i0+i, j0+j
if (0<=i1<x) and (0<=j1<y) and not used[i1][j1] and search_around(i1,j1,t,used):
return True
used[i0][j0] = False
return False
elif t >= n-1 and board[i0][j0] == word[n-1]:
return True
else:
return False
x, y = len(board), len(board[0])
n = len(word)
used=[[False]*y for _ in range(x)]
for i in range(x):
for j in range(y):
if search_around(i, j, 0, used):
return True
return False
回溯算法,定义一个矩阵used用来记录矩阵中元素是否被使用过。定义函数seach_around用来从一个元素开始向周围搜索目标词。具体方法为,首先判断输入的第一个字母与目标词第一个字母是否一致,若是,则标记该位置为已使用过,向四周继续搜索下一位字母,搜索结束后应将标记去除。遍历一遍矩阵,尝试使用每个元素作为搜索起点,若有一个位置成功匹配,则返回True,否则返回False。
我的解法:
class Solution:
def search(self, nums: List[int], target: int) -> bool:
n = len(nums)
left, right = 0, n-1
while left<=right:
mid = (left+right)//2
if nums[mid] == target:
return True
if nums[left] > nums[mid]:
if nums[mid] < target <= nums[right]:
left = mid+1
else:
right = mid-1
elif nums[left]<nums[mid]:
if nums[left] <= target < nums[mid]:
right = mid-1
else:
left = mid+1
else:
left += 1
continue
return False
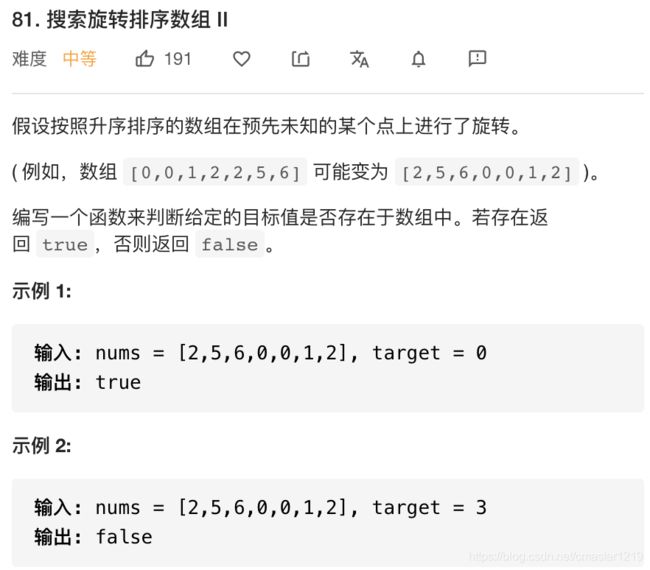
这道题是‘33.搜索旋转列表’的变体,区别在于该题旋转列表中可能存在重复值,这可能造成由nums[mid]与nums[left]的大小关系判断哪一侧为有序数组时,可能出现nums[mid]与nums[left]相等的情况,此时需要移动左指针直到对应元素与nums[mid]不想等为止,此后即可按照与‘33.搜索旋转列表’相同的方式进行二分查找。由于需要逐格移动指针,最坏时间复杂度为O(n)。
我的解法:
class Solution:
def numDecodings(self, s: str) -> int:
def valid_coding(code):
return code[0]!='0' and 0<int(code)<=26
n = len(s)
nd = [1]*(n+1)
nd[1] = 1 if s[0]!='0' else 0
for i in range(2, n+1):
if s[i-1] == '0':
if not valid_coding(s[i-2:i]):
return 0
else:
nd[i] = nd[i-2]
else:
if valid_coding(s[i-2:i]):
nd[i] = nd[i-2] + nd[i-1]
else:
nd[i] = nd[i-1]
return nd[n]
动态规划算法。首先定义一个函数valid_coding,用来判断代入的字符是否是合格的编码。用nd[i]来表示前i个共有的编码方式,一般的状态转移方式为:当遍历到的元素与前一元素可以结对时,nd[i] = nd[i-1] + nd [i-2];当不能结对时,nd[i] = nd[i-1]。因此我们需要得到i=1和i=2两个特解,我们设置np[0]=1,这样nd[2]可以根据转换方式由nd[1]求得,nd[1]当编码第一个元素非零时为1否则为0。比较特殊的是,当编码元素为0时,如果0无法与前一个元素结对,则该编码无效,直接返回0;若可以结对那么np[i]=np[i-2]。依次计算出所有np取值后,np数组最后一个元素即为结果。时间复杂度O(n)。