315 计算右侧小于当前元素的个数

使用计数法，维护一个cnt计数数组，从右往左遍历原数组

对于nums中的每个元素i，出现一次，则++cnt[i]
由于要求右边比其小的元素个数，所以即求cnt[i - 1] + cnt[i - 2] + …
这两个问题刚好对应 307题 的 update 和 sumRange操作，可以用树状数组解决（代码中不需要存cnt数组）

与307题不同的是，此题需要将nums中的元素作为树状数组的下标，由于我们不知道nums中的元素情况
比如是否有负数，负数不能作为下标，比如若有一个元素很大很大，则我们的树状数组要开的很大，会造成很多不必要的浪费

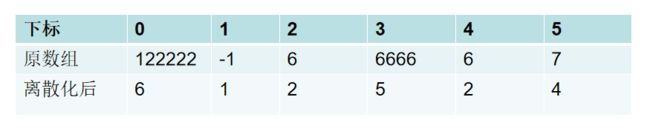
所以需要对原数组离散化，将原数组中的元素与1到num.size()一一对应起来，而不改变元素间的大小关系，不会影响最终的结果。

#include 
using namespace std;

struct node
{
     
    int pos; // 存放原始序号
    int val; // 存放原始值
};

class Solution {
     
    vector<int> tree; // 树状数组
public:
    vector<int> countSmaller(vector<int>& nums) {
     
        // 离散化部分
        vector<node> temp;
        for(int i = 0; i < nums.size(); ++i)
            temp.push_back({
     i, nums[i]});

        // 按val从小到大排序
        sort(temp.begin(), temp.end(), [&](const node a, const node b){
     
            return a.val < b.val;
        });

        if(nums.size()) nums[temp[0].pos] = 1; // 最小的对应为1
        for(int i = 1; i < nums.size(); ++i)
        {
     
            // 与前一个元素值相等，则映射的值也相等
            if(temp[i].val == temp[i - 1].val) nums[temp[i].pos] = nums[temp[i - 1].pos];
            else nums[temp[i].pos] = i + 1;
        }

        // 下面是树状数组部分
        tree.resize(nums.size() + 1); // 树状数组下标为1 - n
        fill(tree.begin(), tree.end(), 0);
        
        vector<int> ans;
        // 由于求的是右侧小于当前元素的个数，所以从后往前遍历
        for(int i = nums.size() - 1; i >= 0; --i) 
        {
     
            update(nums[i]); // nums[i]出现的次数+1
            ans.push_back(sumRange(nums[i] - 1)); // 计算的是小于所以要-1
        }

        reverse(ans.begin(), ans.end()); // 由于从后往前求的，所以要反过来
        return ans;
    }

    inline int lowbit(int x)
    {
     
        return x & (-x);
    }

    void update(int i) // 将i位置元素出现的次数+1，向后更新
    {
     
        for(int j = i; j < tree.size(); j += lowbit(j))
            ++tree[j];
    }

    int sumRange(int i) // 计算i位置（包括i位置）之前的元素和，向前更新
    {
     
        int sum  = 0;
        for(int j = i; j >= 1; j -= lowbit(j))
            sum += tree[j];
        return sum;
    }
};