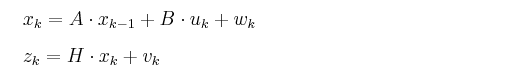OpenCV目标跟踪（五）-kalman滤波器

在实际的运动跟踪中，由于环境因素或者别的原因总会有一些噪声的存在，这样的跟踪效果就会变差，人们想到尽可能多的去利用测量结果来估计运动。这样，任务就可以分为两个阶段：第一阶段，即预测阶段，用过去得到的信息进一步修正以取得目标的下一个将会出现的位置。第二阶段，即校正阶段，我们获得一个测量，然后与基于前一次测量的预期值进行调整。
基于以上的任务，匈牙利数学家kalman提出了kalman滤波器的思想，这个滤波器背后的数学原理，有点复杂，这里给出了两个博客链接，他们都给出了对kalman滤波器数学原理的通俗解释。
http://www.cnblogs.com/feisky/archive/2009/11/09/1599247.html
http://blog.csdn.net/ilyhlf5201314/article/details/8255620

其中最为主要的是如下两个方程：
　

第一个方程是系统的运动方程，第二个方程是系统的观测方程，其中的参数A,B,H,都是矩阵，而OpenCV中自带的kalman示例程序的编程思路也是依据上面的两个方程。
具体的编程主体思路大致是这样的：
（1）初始化以下的变量：测量矩阵，转移矩阵，过程噪声协方差矩阵，测量噪声协方差矩阵，后验错误协方差矩阵等，而这些的矩阵的初始化，即是跟上述的两个方程中的A,B,H相关。
（2）调用OpenCV中的cvKalmanPredict（）函数，这个函数完成的正是任务一，预测阶段。
（3）调用OpenCV中的cvKalmanCorrect（）函数，这个函数完成的是任务二，校正阶段。
（4）重复步骤2和3，直至完成kalman滤波过程。

下面给出具体的kalman滤波示例，主题编程思路遵循上面所说的，但编程也有适当的技巧。示例程序如下：

#include "opencv2/video/tracking.hpp"
#include "opencv2/highgui/highgui.hpp"

#include 

using namespace cv;

static inline Point calcPoint(Point2f center, double R, double angle)
{
    return center + Point2f((float)cos(angle), (float)-sin(angle))*(float)R;
}



int main(int, char**)
{
    /*
    使用kalma步骤一
    下面语句到for前都是kalman的初始化过程，一般在使用kalman这个类时需要初始化的值有：
    转移矩阵，测量矩阵，过程噪声协方差，测量噪声协方差，后验错误协方差矩阵，
    前一状态校正后的值，当前观察值
    */


    Mat img(500, 500, CV_8UC3);
    KalmanFilter KF(2, 1, 0);
    Mat state(2, 1, CV_32F); /* (phi, delta_phi) */
    Mat processNoise(2, 1, CV_32F);
    Mat measurement = Mat::zeros(1, 1, CV_32F);
    char code = (char)-1;

    for (;;)
    {
        randn(state, Scalar::all(0), Scalar::all(0.1));//产生均值为0，标准差为0.1的二维高斯列向量
        KF.transitionMatrix = *(Mat_<float>(2, 2) << 1, 1, 0, 1);//转移矩阵为[1,1;0,1]

        //函数setIdentity是给参数矩阵对角线赋相同值，默认对角线值值为1
        setIdentity(KF.measurementMatrix);
        setIdentity(KF.processNoiseCov, Scalar::all(1e-5));//系统过程噪声方差矩阵
        setIdentity(KF.measurementNoiseCov, Scalar::all(1e-1));//测量过程噪声方差矩阵
        setIdentity(KF.errorCovPost, Scalar::all(1));//后验错误估计协方差矩阵

        //statePost为校正状态，其本质就是前一时刻的状态
        randn(KF.statePost, Scalar::all(0), Scalar::all(0.1));

        for (;;)
        {
            Point2f center(img.cols*0.5f, img.rows*0.5f);
            float R = img.cols / 3.f;
            //state中存放起始角，state为初始状态
            double stateAngle = state.at<float>(0);
            Point statePt = calcPoint(center, R, stateAngle);


            /*
            使用kalma步骤二
            调用kalman这个类的predict方法得到状态的预测值矩阵
            */


            Mat prediction = KF.predict();
            //用kalman预测的是角度
            double predictAngle = prediction.at<float>(0);
            Point predictPt = calcPoint(center, R, predictAngle);

            randn(measurement, Scalar::all(0), Scalar::all(KF.measurementNoiseCov.at<float>(0)));

            // generate measurement
            //带噪声的测量
            measurement += KF.measurementMatrix*state;

            double measAngle = measurement.at<float>(0);
            Point measPt = calcPoint(center, R, measAngle);

            // plot points
            //这个define语句是画2条线段(线长很短)，其实就是画一个“X”叉符号

#define drawCross( center, color, d )                                 \
                line( img, Point( center.x - d, center.y - d ),                \
                             Point( center.x + d, center.y + d ), color, 1, CV_AA, 0); \
                line( img, Point( center.x + d, center.y - d ),                \
                             Point( center.x - d, center.y + d ), color, 1, CV_AA, 0 )

            img = Scalar::all(0);
            //状态坐标白色
            drawCross(statePt, Scalar(255, 255, 255), 3);
            //测量坐标蓝色
            drawCross(measPt, Scalar(0, 0, 255), 3);
            //预测坐标绿色
            drawCross(predictPt, Scalar(0, 255, 0), 3);
            //真实值和测量值之间用红色线连接起来
            line(img, statePt, measPt, Scalar(0, 0, 255), 3, CV_AA, 0);
            //真实值和估计值之间用黄色线连接起来
            line(img, statePt, predictPt, Scalar(0, 255, 255), 3, CV_AA, 0);


            /*
            使用kalma步骤三
            调用kalman这个类的correct方法得到加入观察值校正后的状态变量值矩阵
            */

            if (theRNG().uniform(0, 4) != 0)
                KF.correct(measurement);

            randn(processNoise, Scalar(0), Scalar::all(sqrt(KF.processNoiseCov.at<float>(0, 0))));
            //不加噪声的话就是匀速圆周运动，加了点噪声类似匀速圆周运动，因为噪声的原因，运动方向可能会改变
            state = KF.transitionMatrix*state + processNoise;

            imshow("Kalman", img);
            code = (char)waitKey(100);

            if (code > 0)
                break;
        }
        if (code == 27 || code == 'q' || code == 'Q')
            break;
    }

    return 0;
}

下面是上述程序运行的效果：