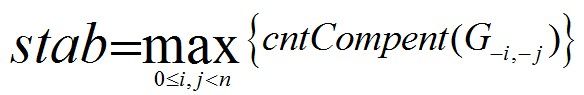TWO NODES(HDU 4587)---去两点最大连通分量数

题目链接

题目描述

Suppose that G is an undirected graph, and the value of stab is defined as follows:

Among the expression,G-i, -j is the remainder after removing node i, node j and all edges that are directly relevant to the previous two nodes. cntCompent is the number of connected components of X independently.
Thus, given a certain undirected graph G, you are supposed to calculating the value of stab.

输入格式

The input will contain the description of several graphs. For each graph, the description consist of an integer N for the number of nodes, an integer M for the number of edges, and M pairs of integers for edges (3<=N,M<=5000).
Please note that the endpoints of edge is marked in the range of [0,N-1], and input cases ends with EOF.

输出格式

For each graph in the input, you should output the value of stab.

输入样例

4 5
0 1
1 2
2 3
3 0
0 2

输出样例

2

分析

题目大意是给定一个无向图，求删去其中的两个顶点后所剩的最大连通分量数。
本题从割点入手：

• 对于第一个顶点我们任意枚举，统计将第一个节点删去后所剩联通分量k。
• 对于第二个顶点我们可以采用tarjan算法统计每个节点删去后的新增联通分量数sum[i]：对于根节点，新增连通分量数=孩子数-1；对于非根节点，新增连通分量数=满足割点条件的次数。

综上，程序的结果应为ans=max(ans,k+sum[i])，另外要特别注意在求统计最大连通分量数时不能省略条件i！= j，原因可以参考这组数据：

4 0

上述数据的正确结果应为2，但省略条件i！= j时的结果为3，因为每个节点都是孤立点，删去这个节点后图的联通分量数会-1，而对于非孤立的点，在删去根节点后至少会保持原图连通分量数不变（孩子数child≥1）。

源程序

tarjan算法

#include 
#define MAXN 5005
#define INF 0x3f3f3f3f
using namespace std;
struct Edge{
     
	int v,next;
	Edge(){
     }
	Edge(int v,int next):v(v),next(next){
     }
}edge[MAXN*2];
int EdgeCount,head[MAXN];
int n,m,cnt;
int dfn[MAXN],low[MAXN],add_block[MAXN];
void addEdge(int u,int v)
{
     
	edge[++EdgeCount]=Edge(v,head[u]);
	head[u]=EdgeCount;
}
void init()
{
     
	memset(dfn,0,sizeof(dfn));
	memset(low,0,sizeof(low));
	memset(add_block,0,sizeof(add_block));
	cnt=0;
}
void tarjan(int u,int pre,int forbid)//forbid为禁止访问点
{
     	
	dfn[u]=low[u]=++cnt;	//时间戳 
	int child=0; 
	for(int i=head[u];i;i=edge[i].next){
     
		int v=edge[i].v;
		if(v==pre||v==forbid)continue;
		if(!dfn[v]){
     	//还未访问过
			child++;
			tarjan(v,u,forbid);
			low[u]=min(low[u],low[v]);	//更新最小时间戳
			if(u!=-1&&low[v]>=dfn[u]){
     	//满足割点要求 
				add_block[u]++;
			}
		}
		else 	//已经访问过且v不是u的父节点 
			low[u]=min(low[u],dfn[v]);
	}
	if(pre<0)	//根节点由于没有父节点的连通分量,故新增连通分量需-1 
		add_block[u]=child-1; 
}
int main()
{
     
	while(~scanf("%d%d",&n,&m)){
     
		memset(head,0,sizeof(head));
		EdgeCount=0;
		for(int i=1;i<=m;i++){
     
			int u,v;
			scanf("%d%d",&u,&v);
			addEdge(u,v);
			addEdge(v,u);
		}
		int ans=-INF;
		for(int i=0;i<n;i++){
     	//枚举第一个割点
			int k=0;	//删除割点后的连通分量数
			init();
			for(int j=0;j<n;j++){
     	//枚举第二个割点 
				if(i!=j&&!dfn[j]){
     	//两个割点不相同且第二个割点还没访问过 
					k++;
					tarjan(j,-1,i); 
				} 
			} 
			for(int j=0;j<n;j++)	//add_block[i]表示删去点i后新增连通分量数 
				if(j!=i)	//注意全为孤点时的情况 
					ans=max(ans,k+add_block[j]);
		}
		printf("%d\n",ans); 
	}
}