堆——以洛谷p3378,p1334,p1628,p1878为例
堆
堆的五个基本操作:
1.在集合中插入一个数 heap[++size]=x ; up[size]
2.求集合当中的最小值 heap[1]
3.删除最小值 heap[1]=heap[size] ; size-- ; down(1)
4.删除任意一元素 heap[k]=heap[size] ; size-- ; down(k) ; up(k)
5.修改任一元素 heap[k]=x ; down(k) ; up(k)
p3378[模板]堆
题目描述
给定一个数列,初始为空,请支持下面三种操作:
- 给定一个整数 x,请将 x 加入到数列中。
- 输出数列中最小的数。
- 删除数列中最小的数(如果有多个数最小,只删除 1 个)
符合模板中的1.2.3操作
输入格式
第一行是一个整数,表示操作的次数 n。
接下来 n 行,每行表示一次操作。每行首先有一个整数 op 表示操作类型。
- 若 op=1,则后面有一个整数 xxx,表示要将 xxx 加入数列。
- 若 op=2,则表示要求输出数列中的最小数。
- 若 op=3,则表示删除数列中的最小数。如果有多个数最小,只删除 1 个。
输出格式
对于每个操作 2,输出一行一个整数表示答案。
输入输出样例
输入 #1复制
5
1 2
1 5
2
3
2输出 #1复制
2
5说明/提示
数据规模与约定
- 对于 30%的数据,保证n<=15
- 对于70%的数据,保证n<10 4
- 对于100%的数据,保证1≤n≤10 6,1≤x<2 31,op∈{1,2,3}
-
解析
#include
#include
#include
using namespace std;
const int N = 1000010;
int h[N], ph[N], hp[N], cnt;
void head_swap(int a, int b)
{
swap(ph[hp[a]], ph[hp[b]]);
swap(hp[a], hp[b]);
swap(h[a], h[b]);
}
void down(int u)
{
int t = u;
if(u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
if(u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
if(u != t)
{
head_swap(u, t);
down(t);
}
}
void up(int u)
{
while(u/2 && h[u/2] > h[u])
{
head_swap(u, u/2);
u >>= 1;
}
}
int main()
{
int n, m = 0;
cin >> n;
while(n--)
{
int op, x;
cin >> op;
if(op == 1)
{
cin >> x;
cnt++;
m++;
ph[m] = cnt, hp[cnt] = m;
h[cnt] = x;
up(cnt);
}
else if(op == 2)
{
printf("%d\n", h[1]);
}
else
{
head_swap(1, cnt);
cnt--;
down(1);
}
}
return 0;
} 代码与模拟堆的题是比较相似的,不同的就是只需要完成前三个基本操作,而且主函数这里是用了条件语句,满足op那里的要求的
p1334 瑞瑞的木板
题目背景
瑞瑞想要亲自修复在他的一个小牧场周围的围栏。
题目描述
他测量栅栏并发现他需要 n 根木板,每根的长度为整数 li。于是,他买了一根足够长的木板,长度为所需的 n根木板的长度的总和,他决定将这根木板切成所需的 n 根木板(瑞瑞在切割木板时不会产生木屑,不需考虑切割时损耗的长度)。
瑞瑞切割木板时使用的是一种特殊的方式,这种方式在将一根长度为 x的木板切为两根时,需要消耗 x个单位的能量。瑞瑞拥有无尽的能量,但现在提倡节约能量,所以作为榜样,他决定尽可能节约能量。显然,总共需要切割 (n−1) 次,问题是,每次应该怎么切呢?请编程计算最少需要消耗的能量总和。
输入格式
输入的第一行是整数,表示所需木板的数量 n。
第 2 到第 (n+1) 行,每行一个整数,第 (i+1)行的整数 l代表第 i 根木板的长度 lil.
输出格式
一个整数,表示最少需要消耗的能量总和。
输入样例
3
8
5
8输出样例
34
说明/提示
输入输出样例 1 解释
将长度为 21 的木板,第一次切割为长度为 8 和长度为 13的,消耗 21 个单位的能量,第二次将长度为 13 的木板切割为长度为 5 和 8 的,消耗 13 个单位的能量,共消耗 34个单位的能量,是消耗能量最小的方案。
解析
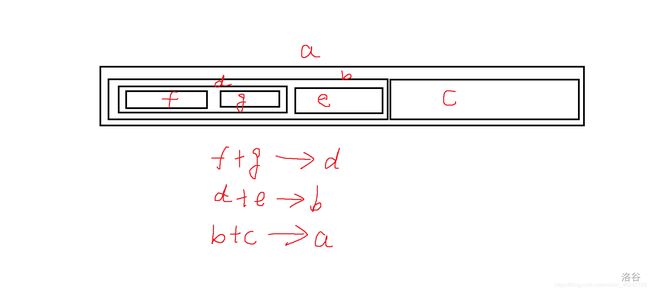
以四块木板为例,来进行n块木板的推广
我们可以知道,割木板的次数是一定的,是N-1次,割长度为x的木板时,能量为x,先假设我们需要如图cegf四种长度的木板,那么现在问题可以转化为如何将这四种木板拼接成一块木板,所需的能量最小。那么我们就可以知道,先fg这两块长度最小的木板相加所需能量最小,将f与g相加之后,问题又可以转化为dec这三块木板拼接,怎样能量最小,同样的道理,找出三块中长度最小的两块相加,能量最小。最后我们根据这四个木板,可以得出普遍的结论了。就是每次取出堆顶的两个元素,将他们的和加入去除这两个元素的新堆中,并更新答案
#include
#include
using namespace std;
int n;
long long l,s[50000],da;//题目数字给的太大了,不开long long过不了。
void up(int u)//上浮,将一个新值按规矩上移(每个子节点都大于它的父亲节点)
{
while(u!=1)//到顶结束
{
int c=u>>1;//位运算,相当于除以2(向下取);
if(s[u]s[c])
t=c;//有左边并且可换
if(s[u]>s[c+1]&&s[c]>s[c+1]&&c+1<=n)
t=c+1;//有右边并且比左边好
if(t!=u)//不等交换
swap(s[u],s[t]);
else//找到位置,不动了
break;
u=t;
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)//这个循环是将木块的长度排成一个堆
{
cin>>l;
s[i]=l;
up(i);
}
for(int i=1;n!=1;i++)//当我节点个数为1时就做完了
{
int k=s[1];
s[1]=s[n--];
down();//删除最小值
k=k+s[1];
s[1]=s[n--];
down();//删除新堆中的最小值
s[++n]=k;
up(n);//将k即两个小值之和插入堆中形成新的堆
da=da+k;//最后是累计答案
}
cout< p1628合并排序
题目描述
有N个单词和字符串T,按字典序输出以字符串T为前缀的所有单词。
输入格式
输入文件第一行包含一个正整数N;
接下来N行,每行一个单词,长度不超过100;
最后一行包含字符串T。
【数据规模】
对于60%的数据,满足1≤N≤1000;
对于100%的数据,满足1≤N≤100000且所有字符均为小写字母;
输出格式
按字典序升序输出答案。
输入样例
6
na
no
ki
ki
ka
ku
k输出样例
ka
ki
ki
ku解析
#include
#include
#include
using namespace std;
int n;
string s[100001], m;
bool check(string s)
{
string x;
for(int i = 0; i < m.length(); i++)//m有多少个字母就将单词中的前多少位提出来
{
x += s[i];
}
if(x == m)//直接比较拼接后的字符串与m是否相等
{
return true;
}
else
{
return false;
}
}
int main()
{
cin>>n;//输入单词的个数n
for(int i = 1; i <= n; i++)//用循环输入n个单词
{
cin >> s[i];
}
cin >> m;//输入字符串m
sort(s + 1, s + n + 1);//STL中自带排序函数sort,sort给给定区间内所有元素进行排序,在这里直接将字母按照字典顺序排好
for(int i = 1; i <= n; i++)
{
if(check(s[i]))//当拼接后的字母与m相等时,则输出
{
cout << s[i] << endl;
}
}
return 0;
} p1878舞蹈课
题目描述
有n个人参加一个舞蹈课。每个人的舞蹈技术由整数来决定。在舞蹈课的开始,他们从左到右站成一排。当这一排中至少有一对相邻的异性时,舞蹈技术相差最小的那一对会出列并开始跳舞。如果不止一对,那么最左边的那一对出列。一对异性出列之后,队伍中的空白按原顺序补上(即:若队伍为ABCD,那么BC出列之后队伍变为AD)。舞蹈技术相差最小即是ai的绝对值最小。
任务是模拟以上过程,确定跳舞的配对及顺序。
输入格式
第一行为正整数n(1<=n<=2*10^5):队伍中的人数。下一行包含n个字符B或者G,B代表男,G代表女。下一行为n个整数ai(ai<=10^7)。所有信息按照从左到右的顺序给出。在50%的数据中,n<=200。
输出格式
第一行:出列的总对数k。接下来输出k行,每行是两个整数。按跳舞顺序输出,两个整数代表这一对舞伴的编号(按输入顺序从左往右1至n编号)。请先输出较小的整数,再输出较大的整数。
输入输出样例
4
BGBG
4 2 4 3
2
3 4
1 2
分析题目后得到以下几个流程:
1.先建一个Bool数组(或者Char数组),用于存放性别
2.输入舞蹈技术值,同时将一对异性入堆(入堆的是舞蹈技术相差)
3.取出堆顶那一对人(理由:小根堆中根最小)
4.保证此时堆顶那一对人不是已经出堆的人
5.讲不上后的队伍再次取出一对异性入堆
6.重复3、4、5,直到堆为空
7.输出
代码
#include
const int maxn = 200010;
struct node{
int value,l,r;
friend bool operator > (node aa,node bb){return aa.value > bb.value || (aa.value == bb.value && aa.l > bb.l);}
}heap[maxn],tmp;
void swap(node &a,node &b){tmp = a,a = b,b = tmp;}
int abs(int value){return value < 0?-value:value;}
//手写swap,abs函数
int n,a[maxn],heap_size,tot,tl[maxn],tr[maxn];
bool b[maxn],f[maxn];
void put(int value,int l,int r){
int now = ++heap_size,next;
heap[heap_size].value = value,heap[heap_size].l = l,heap[heap_size].r = r;
while(now > 1){
next = now >> 1;
if(heap[now] > heap[next]) return;
swap(heap[now],heap[next]);
now = next;
}
}
void get(){
int now = 1,next;
heap[1].value = heap[heap_size].value,heap[1].l = heap[heap_size].l,heap[1].r = heap[heap_size--].r;
while(now << 1 <= heap_size){
next = now << 1;
if(next < heap_size && heap[next] > heap[next + 1]) next++;
if(heap[next] > heap[now]) return;
swap(heap[now],heap[next]);
now = next;
}
}
int main(){
scanf("%d\n",&n);
for(int i = 0;i < n;i++){
char ch = getchar();
f[i] = ch == 'B';//若这个人他是'B'置f[i]为true,反之亦反
}//巧妙地输入情况
for(int i = 0;i < n;i++){
scanf("%d",&a[i]);//输入舞蹈技术
int j = i - 1;//置j为i前面那个人
if(i && f[i] ^ f[j]) put(abs(a[i] - a[j]),j,i);
//如果i不是指向第一个人,且f[i] != f[j],将舞蹈技术值差和两个人的下标入堆
}
while(heap_size){
int l = heap[1].l,r = heap[1].r,ll,rr;//当前最小的那一对出堆
b[l] = b[r] = true;
tl[++tot] = l + 1,tr[tot] = r + 1;
do{
get();
if(!heap_size) break;
ll = heap[1].l,rr = heap[1].r;
}while(b[ll] || b[rr]);//此操作维护该堆直至堆顶不为已出堆的元素
while(l >= 0 && b[l]) l--;
while(r < n && b[r]) r++; //寻找空白两边的元素
if(l >= 0 && r < n && f[l] ^ f[r]) put(abs(a[l] - a[r]),l,r);//将其入堆
}
printf("%d",tot);
for(int i = 1;i <= tot;i++) printf("\n%d %d",tl[i],tr[i]); //输出答案
return 0;
}