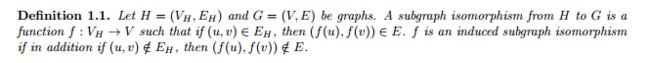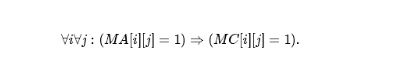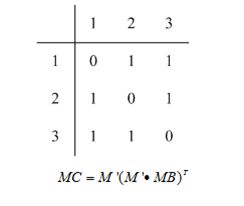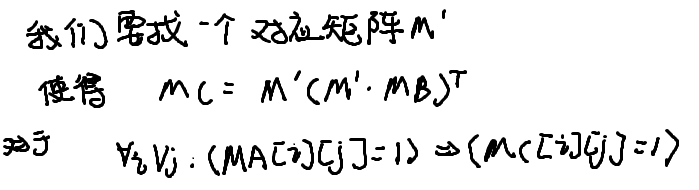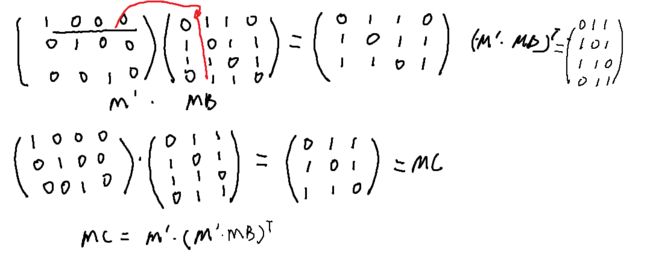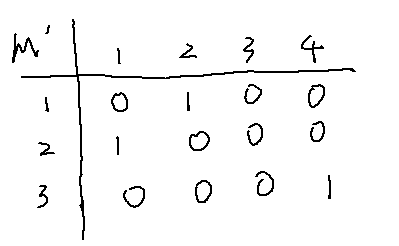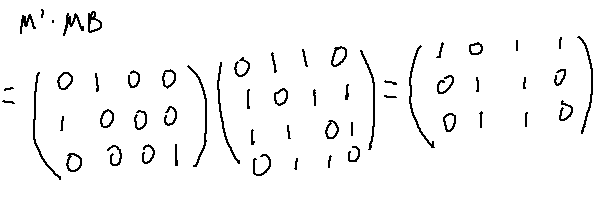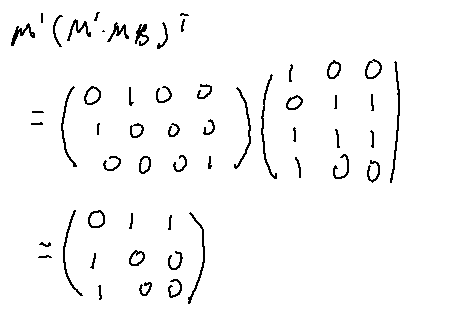子图同构问题与Ullmann Algorithm 算法(一)
目录索引
- 目录索引
- 写在前面的话
- 子图同构定义
- 子图同构的映射关系
- Reference
- 写在后面的话
写在前面的话
谨以此片献给 my best love, grandpa.
时光匆匆流逝,我们永远无能为力,我能做的就是脚踏实地,变成你的骄傲~和你在一起的时光,是我所有的宝藏。从你身上继承的美好品质,我要努力把它变得更加迷人。如果时空真的可以扭转,我希望有个奇点,我们可以一直在一起不分开。
1.子图同构定义
我使用的定义是来自这篇参考文献:
http://theory.stanford.edu/~virgi/cs267/lecture1.pdf
假设有两个图 H=(VH,EH) 和图 G=(V,E) 子图 同构即从H到G存在这样一个函数 f:VH→V 并且 (u,v)∈EH 使得 (f(u),f(v))∈E 同样成立 f 叫做子图同构的一个映射。
不过我觉得wiki讲的更好,子图同构定义
是英文的,如果你看英文不成问题的话,可以仔细看。
我觉得看英文的这个还是很锻炼的,毕竟我们不是native speaker.
2.子图同构的映射关系
说明,在这里的图,我们考虑的是没有标签的图。只有顶点序号的图。
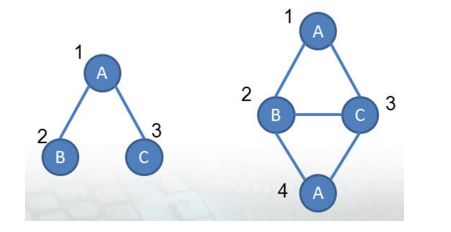
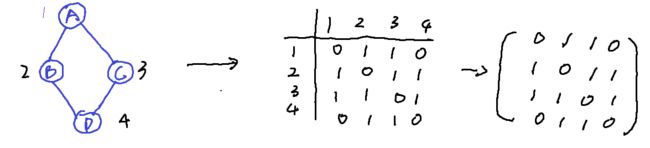
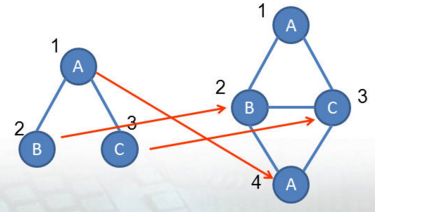
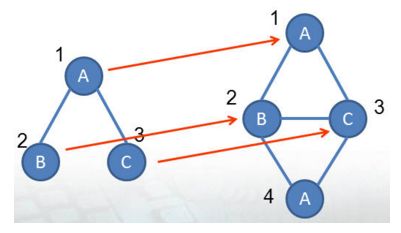
如下图,左图与右图子图同构:
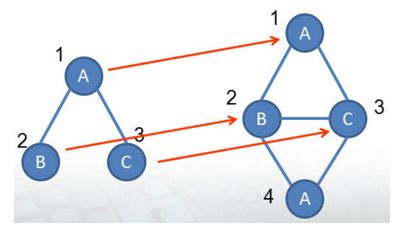
我们看一下他们存在的一种映射关系:
我们把左边的图叫做图 A ,把右边的图叫做图 B
用 MA,MB 分别表示左图 A, 和右图 B 的对应的邻接矩阵,其中 MA[i][j]=1 表示顶点 vi 与 vj 存在一条边, A[i][j]=0 表示无边. M' 表示映射g从 MA 到 MB 的映射矩阵, M'[i][j]=1 表示 A 中第 i 个顶点 vi 对应到 MB 中的第 j 个顶点,否则为0表示没有对应
根据我们上面的例子,我们来描述一下在Ullmann algorithm 算法中的一个定理
定理1:
如果图 A 关于映射 f 子图同构与图 B ,令
其中T表示的是矩阵的转置。
在A矩阵中是1的地方在C矩阵中也要为1
根据定理一 MC=M′(M′MB)T 我们可以计算得到MC的矩阵值:
所以我们找到的映射矩阵 M′ 是一个满足图 A 和图 B 子图同构的矩阵。
下面我们来亲自实践一遍这个过程:
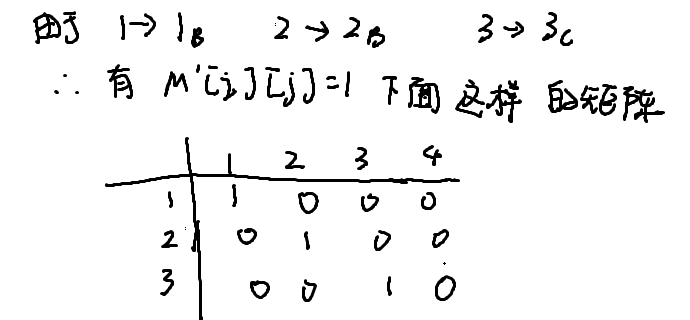
由于这两个图的子图同构的映射比较好找出来,刚才我们就找出来一组,就是这个例子,
那我我们可以很容易的构建出子图同构的映射矩阵 M' 。
下面我们要做的事情就是看有没有这样一个MC 满足我们的定理1。
我们找的映射矩阵完全满足我们的要求能构造出我们的MC,其实MC对应的就是我们的矩阵MB当中的一块,如果你仔细观察可以发现:
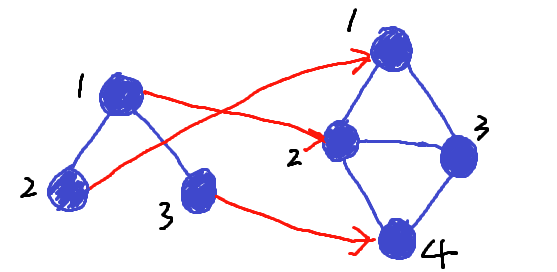
我们发现其实第4列和第1列是完全一致的,这个时候调换一下位置,可以发现下面的规律:
这个时候我们可以找到另外一种映射关系,如下图所示:
那么,这个时候问题就来了,有没有下面这种可能呢:
那么它对应的映射矩阵就是下面这个样子的:
我们来亲自实践一下:
这个时候我们发现我们找到的MC是满足定理1的,那就是我们找的映射矩阵是其中的一个同构映射。
其实根据图论中的子图同构的定义,我们发现,只要点对点,边对边是一致的,那么这两个图就是子图同构,他是NPC(NP complete)问题。
如果我们的图是没有被设置标签的,标签就是图中的A,B,C这些,在有的时候如果我们的图已经被设置了标签,那就要求两个比较的图的点对点,边对边,标签对标签要形成双射,也就是单射和满射。
如果这样的情况,就像下面两个博客说的一样是存在两个映射,如果这个图的点或者是边没有被设置标签,那么和图 A 它同构的子图就要很多我们可以在图 B 中找到。
http://www.cnblogs.com/huadongw/p/4154295.html
http://blog.csdn.net/luo123n/article/details/49787183
并不是只有两个子图同构的映射,这两个图中有很多的子图同构的映射。
Reference
http://www.cnblogs.com/huadongw/p/4154295.html
今天写这个花了两个小时,手已经抓了
写在后面的话
我望着碧海蓝天 看云朵在兜圈
慢慢兜成你的淘气鬼脸 忽近忽远
微风在摇手轻吹 阳光睡在我的右侧脸
我笑着脸去迎接 你给的誓~言
YA~~~~~~~
没发现 紫外线 太强烈 我爱你没有防备
等你牵手带着我漫游世界 幸福快乐瞬间一起体会
没发现 紫外线 太强烈 后知后觉的逃远
我们躲在秘密的空中花园 爱情蝴蝶也和我们相约
眼圈熬成黑看你更深邃
只怕还不够爱 Time’s going by