最小生成树——prim算法
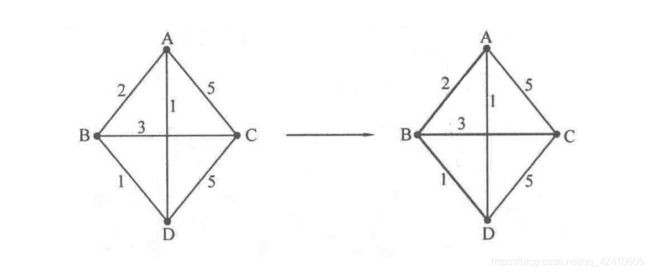
最小生成树(Minimum Spanning Tree,MST)是在一个给定的无向图G(V,E)中求一棵树T,使得这棵树拥有图G中的所有顶点,且所有边都是来自图G中的边,并且满足整棵树的边权之和最小。下图给出了一个图G及其最小生成树T,其中较粗的线即为最小生成树的边。可以看到,边AB、BC、BD包含了图G的所有顶点,且由它们生成的树的边权之和为6,是所有生成树中权值最小的。
最小生成树有3个性质需要掌握:
①最小生成树是树,因此其边数等于顶点数减1,且树内一定不会有环。
②对给定的图G(V,E),其最小生成树可以不唯一,但其边权之和一定是唯一的。
③由于最小生成树是在无向图上生成的,因此其根结点可以是这棵树上的任意一个结点。于是,,如果题目中涉及最小生成树本身的输出,为了让最小生成树唯一,一般都会直接给出根结点,读者只需以给出的结点作为根结点来求解最小生成树即可。
求解最小生成树一般有两种算法,即prim算法与kruskal算法。这两个算法都是采用了贪心法的思想,只是贪心的策略不太一样。
prim算法(读者可以将其读作“普里姆算法”)用来解决最小生成树问题,其基本思想是对图G(V,E)设置集合S,存放已被访问的顶点,然后每次从集合V-S中选择与集合S的最短距离最小的一个顶点(记为u),访问并加入集合S。之后,令顶点u为中介点,优化所有从u能到达的顶点v与集合S之间的最短距离。这样的操作执行n次(n为顶点个数),直到集合S已包含所有顶点。可以发现,prim算法的思想与最短路径中Dijkstra算法的思想几乎完全相同,只是在涉及最短距离时使用了集合S代替 Dijkstra算法中的起点s。
①将地图上的所有边都抹去,只有当访问一个顶点后オ把这个顶点顶点连接的边显现(这点和Dijkstra算法中相同)。
②将已访问的顶点置于ー个巨型防护罩中。可以沿着这个防护罩连接的边去访问未到达的顶点
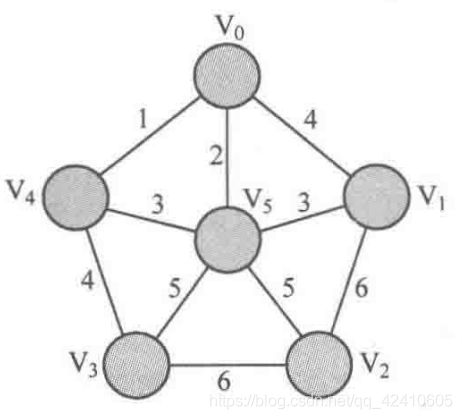
③在地图中的顶点V(0≤i≤5)上记录顶点V与巨型防护罩之间的最短距离(即V与每个访问的顶点之间距离的最小值)。由于在①把所有边都抹去了,因此在初始状态下只在顶点V0上标记0,而其他顶点都标记无穷大(记为INF)。为了方便叙述,在下文中某几处出现的最短距离都是指从顶点V与当前巨型防护罩之间的最短距离。
下面是行动策略:
①由于要访问六个顶点,因此将②③步骤执行六次,每次访问一个顶点(如果是n个顶点,那么就执行n次)。
②每次都从还未访问的顶点中选择与当前巨型防护罩最近的顶点(记为Vk(0≤k≤5)),使用“爆裂模式”的能力恢复这条最近的边(并成为最小生成树中的一条边),前往访问。
③访问顶点Vk后,将Vk加入巨型防护罩中,开放地图上Vk连接的所有边,并査看以Vk作为巨型防护罩连接外界的接口的情况下,能否利用Vk刚开放的边使某些还未访问的顶点与巨型防护罩的最短距离变小。如果能,则将那个最短距离覆盖到地图对应的顶点上。
另外,为了得到最小生成树的边权之和,需要在访问顶点之前设置一个初值为0的变量sum,并在攻打过程中将加入最小生成树中的边的边权累加起来。
prim算法解决的是最小生成树问题,即在一个给定的无向图G(V,E)中求一棵生成树T,使得这棵树拥有图G中的所有顶点,且所有边都是来自图G中的边,并且满足整棵树的边权之和最小。prim算法的基本思想是对图G(V,E)设置集合S(即巨型防护罩)来存放已被访问的顶点,然后执行n次下面的两个步骤(n为顶点个数)。
①每次从集合V-S(即未访问的顶点)中选择与集合S(巨型防护罩)最近的一个顶点(记为u),访问u并将其加入集合S(加入巨型防护罩),同时把这条离集合S最近的边加入最小生成树中。
②令顶点u作为集合S与集合V-S连接的接口(即把当前访问的顶点作为巨型防护罩与外界的接口),优化从u能到达的未访问顶点v与集合S(巨型防护罩)的最短距离。
prim算法的具体实现:
prim算法需要实现两个关键的概念,即集合S的实现、顶点V(0≤i≤n-1)与集合S(巨型防护罩)的最短距离。
①集合S的实现方法和Dijkstra中相同,即使用一个bool型数组vis[]表示顶点是否已被访问。其中vis[i]=true表示顶点V[i]已被访问,vis[i]= false则表示顶点V未被访问。
②不妨令int型数组d[]来存放顶点Vi(0≤i≤n-1)与集合S(巨型防护罩)的最短距离。初始时除了起点s的d[s]赋为0,其余顶点都赋为一个很大的数来表示INF,即不可达。
可以发现,prim算法与Dijkstra算法使用的思想几乎完全相同,只有在数组的含义上有所区别。其中,Dijkstra算法的数组d[]含义为起点s到达顶点伍的最短距离,而prim算法的数组d[]含义为顶点Vi与集合S的最短距离,两者的区别仅在于最短距离是顶点i针对“起点s”还是“集合S”。另外,对最小生成树问题而言,如果仅是求最小边权之和,那么在prim算法中就可以随意指定一个顶点为初始点,例如在下面的代码中将默认使用0号顶点为初始点。
根据上面的描述,可以得到下面的伪代码(注意与prim算法基本思想进行联系):
//G为图, 一般设置为 全局变量;数组d为顶点与集合S的最短距离
Prim(G,d[]){
初始化;
for(循环n次){
u = 使d[u]最小的还未被访问的顶点的标号;
记u已被访问;
for(从u出发能到达的所有顶点v){
if(v未被访问&&以u为中介点使得v与集合S的最短距离d[v]更优]){
将G[u][v]赋值给v与集合S的最短距离d[v];
}
}
}
}和Dijkstra算法的伪代码进行比较后发现,Dijkstra算法和prim算法只有优化d[v]的部分不同,而其他语句都是相同的。这再次说明:Dijkstra算法和prim算法实际上是相同的思路,只不过是数组的含义不同罢了。在了解了上面这点之后,读者可以参照 Dijkstra算法的写法很容易地写出prim算法的代码,而在此之前,需要先定义MAXV为最大顶点数、INF为一个很大的数字:
const int MAXV = 100; //MAXV为最大顶点数
const int INF = 1000000000; //INF是一个很大的数
下面给出分别使用邻接矩阵和邻接表的prim算法代码。
(1)邻接矩阵版。
int n,G[MAXV][MAXV]; //n为顶点数,MAXV为最大顶点数
int d[maxv]; //顶点与几个S的最短距离
bool vis[MAXV] = {false}; //标记数组,vis[i]==true表示已访问。初始值均为false
int prim(){ //默认0号为初始点,函数返回最小生成树的边权之和
fill(d,d+MAXV,INF); //fill函数将整个d数组赋值为INF(慎用memset)
d[0] = 0; //只有0号顶点到集合S的距离为0,其余全为INF
int ans = 0; //存放最小生成树的边权之和
for(int i=0;i(2)邻接表版。
vector Adj[MAXV]; //图 G,Adj[u]存放从顶点u出发可以到达的所有顶点
int n; // n为顶点数,图G使用邻接表实现,MAXV为最大顶点数
int d[maxv]; //顶点与集合S的最短距离
bool vis[MAXV] = {false}; //标记数组,vis[i]==true表示已访问。初始值均为false
int prim(){ //s为起点
fill(d,d+MAXV,INF); //fill函数将整个d数组赋值为INF(慎用memset)
d[0] = 0; //只有0号顶点到集合S的距离为0,其余全为INF for(int i=0;i 和Dijkstra算法一样,使用这种写法的复杂度是O(V^2),其中邻接表实现的prim算法可以通过堆优化使时间复杂度降为 O(VlogV+E)。另外,O(V^2)的复杂度也说明,尽量在图的顶点数目较少而边数较多的情况下(即稠密图上)使用prim算法。
下面是本节讲解的图例题代码:
#include
#include
using namespace std;
const int MAXV = 1000; //最大顶点数
const int INF = 1000000000; //设INF为一个很大的数
int n,m,s,G[MAXV][MAXV]; //n为顶点数,m为边数,s为起点
int d[MAXV]; //顶点与集合S的最短距离
bool vis[MAXV] = {false}; //标记数组,vis[i]==true表示已访问。初始值均为false
int prim(){ //s为起点
fill(d,d+MAXV,INF); //fill函数将整个d数组赋值为INF(慎用memset)
d[0] = 0; //只有0号顶点到集合S的距离为0,其余全为INF
int ans = 0; //存放最小生成树的边权之和
for(int i=0;iv的边权
G[u][v] = G[v][u] = w; //无向图
}
int ans = prim(); // prim算法入口
printf("%d\n",ans);
return 0;
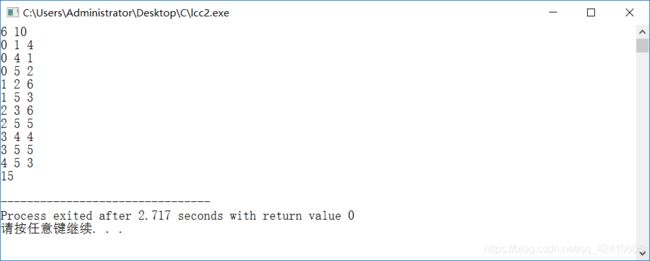
} 输入数据:
6 10
0 1 4
0 4 1
0 5 2
1 2 6
1 5 3
2 3 6
2 5 5
3 4 4
3 5 5
4 5 3输出结果: