set集合容器
set集合容器
一、原理
set集合容器使用一种称为红黑树(Red-Black Tree)的平衡二叉检索树的数据结构,来组织泛化的元素数据。每个节点包含一个取值红色或黑色的颜色域,以利于进行树的平衡处理。作为节点键值的元素的插入,必须确保每个子树根节点的键值大于左子树所有节点的键值,而小于右子树所有节点的键值。不会将重复的键值插入容器,也不需指定具体的插入位置,而按元素在树中的关联关系,进行位置检索和插入,元素的删除亦然。
元素数据的检索,使用的是二叉检索树的中序遍历算法,检索的效率高于vector、deque和 list 等容器。由于采用中序遍历算法可将二叉检索树的键值,由小到大排列遍历出来,因此set集合容器蕴含了元素间的有序性。
1、红黑树的定义
如下是红黑树在二叉检索树基础上所作的补充定义,可以看到C++ STL的红黑树对标准红黑树略作修改,不要求叶子节点必须是黑色。
(1)根节点是黑色。
(2)其他节点是红色或黑色。
(3)每个红色节点的左、右节点必须是黑色。
(4)每条从叶子节点到根节点的路径,都包含相同数目的黑色节点。
可见,红黑树使用红黑二色进行“着色”,目的是利用颜色值做二叉树的平衡对称性的检查,只要插入的节点“着色”满足红黑二色的规定,最短路径与最长路径不会相差太远,红黑树的节点分布就能大体上达至平衡。当然,这种平衡是一种有所放宽的平衡。
由性质(3)可得出,红黑树的任何路径都不会出现两个相邻的红色节点,否则存在一对父子节点都是红色。
由性质(4),可设从根节点到叶节点路径上的黑色节点数均为n,于是,红黑树的最短路径为全黑的“黑→黑→…→黑”路径,即最短路径长度为n?1(相邻节点间的距离为1)。而最长路径只能取为红黑交替的“黑→红→黑→红→…→黑”路径,这样可使黑色节点数最多,即最长路径为2(n?1)。所以在红黑树的所有从根节点到叶子节点的路径中,最长路径不会超过最短路径的2倍。
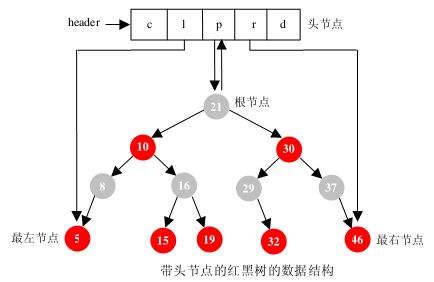
2、结构
将一组整数21、30、10、8、37、46、29、5、16、19、15和32依次插入生成一个红黑树。如图所示,先构造一个黑色节点21作为根,由于30>21,因此30作为21的右节点插入,10<21,10作为21的左节点插入。
元素检索的时间复杂度是log2n(n为元素个数)。
3、说明
红黑树的插入和删除都要涉及类似平衡二叉树如何进行平衡问题。关于平衡二叉树,我们可以参见:
http://blog.163.com/zhoumhan_0351/blog/static/399542272009104113331705
关于红黑树调整代码,可以参见SGI的stl_tree文件中。附中有一部分关键的。
二、应用
1、创建
(1)set()用默认的less函数对象和内存分配器,创建一个没有任何数据元素的set对象。
set
(2)set(const key_compare& comp)
指定一个比较函数对象comp来创建set对象,内存分配器为默认值。
//定义字符串比较函数对象strLess
struct strLess{
bool operator()(const char* s1, const char* s2) const
{ return strcmp(s1, s2) < 0;}
};
//创建set容器对象s
set
(3)set(const set&)
set拷贝构造函数,通过红黑树的拷贝构造函数,实现两个set容器的元素、头节点和节点个数的拷贝。
//set
set
(4)set(InputIterator first, InputIterator last)
用迭代器区间[first,last)所指的元素,创建一个set对象。
int iArray[] = { 13, 32, 19 };
set
(5)set(InputIterator first, InputIterator last, const key_compare& comp)
用迭代器区间[first, last)所指的元素和 comp 函数对象,创建一个 set 对象。
const char* szArray[] = { "hello", "dog", "bird" };
set
2、插入
(1)pair
将元素v插入set容器,要求v值不与set容器的任何元素重复,否则插入失败。返回一个pair配对对象,提供所插入元素的迭代器位置和true/false插入成功标志。
(2)iterator insert(iterator position, const value_type& v)
将元素v插入set容器,参数position只是提示可在position位置之前插入v,所返回的插入位置视实际情况而定,不一定能在position位置前插入。
(3)void insert(InputIterator first, InputIterator last)
将某迭代器区间[first,last)所指的数据作为元素,插入到set容器。
3、访问
(1)iterator begin()//通过迭代器的“++”进行中序遍历
(2)iterator end()
及反向迭找器
4、寻找
const_iterator find(const Key& key) const;
5、其它
其它函数,如删除erase,empty,size,swap,等,基本用法同其它的容器,可参考相关的C++文档,如MSDN。
三、例子
#include "set.h"
#include "iostream"
using namespace std;
int main()
{
set
s.insert(10);
s.insert(11);
s.insert(12);
s.insert(13);
set
for(i=s.begin();i!=s.end();i++)
cout<<(*i)<<" ";
return 1;
}
附:SGI中红黑树的调整代码
_Rb_tree_rotate_left(_Rb_tree_node_base* x, _Rb_tree_node_base*& root)
{
_Rb_tree_node_base* y = x->_M_right;
x->_M_right = y->_M_left;
if (y->_M_left !=0)
y->_M_left->_M_parent = x;
y->_M_parent = x->_M_parent;
if (x == root)
root = y;
else if (x == x->_M_parent->_M_left)
x->_M_parent->_M_left = y;
else
x->_M_parent->_M_right = y;
y->_M_left = x;
x->_M_parent = y;
}
inline void
_Rb_tree_rotate_right(_Rb_tree_node_base* x, _Rb_tree_node_base*& root)
{
_Rb_tree_node_base* y = x->_M_left;
x->_M_left = y->_M_right;
if (y->_M_right != 0)
y->_M_right->_M_parent = x;
y->_M_parent = x->_M_parent;
if (x == root)
root = y;
else if (x == x->_M_parent->_M_right)
x->_M_parent->_M_right = y;
else
x->_M_parent->_M_left = y;
y->_M_right = x;
x->_M_parent = y;
}
inline void
_Rb_tree_rebalance(_Rb_tree_node_base* x, _Rb_tree_node_base*& root)
{
x->_M_color = _M_red;
while (x != root
&& x->_M_parent->_M_color == _M_red)
{
if (x->_M_parent == x->_M_parent->_M_parent->_M_left)
{
_Rb_tree_node_base* y = x->_M_parent->_M_parent->_M_right;
if (y && y->_M_color == _M_red)
{
x->_M_parent->_M_color = _M_black;
y->_M_color = _M_black;
x->_M_parent->_M_parent->_M_color = _M_red;
x = x->_M_parent->_M_parent;
}
else
{
if (x == x->_M_parent->_M_right)
{
x = x->_M_parent;
_Rb_tree_rotate_left(x, root);
}
x->_M_parent->_M_color = _M_black;
x->_M_parent->_M_parent->_M_color = _M_red;
_Rb_tree_rotate_right(x->_M_parent->_M_parent, root);
}
}
else
{
_Rb_tree_node_base* y = x->_M_parent->_M_parent->_M_left;
if (y && y->_M_color == _M_red)
{
x->_M_parent->_M_color = _M_black;
y->_M_color = _M_black;
x->_M_parent->_M_parent->_M_color = _M_red;
x = x->_M_parent->_M_parent;
}
else
{
if (x == x->_M_parent->_M_left)
{
x = x->_M_parent;
_Rb_tree_rotate_right(x, root);
}
x->_M_parent->_M_color = _M_black;
x->_M_parent->_M_parent->_M_color = _M_red;
_Rb_tree_rotate_left(x->_M_parent->_M_parent, root);
}
}
}
root->_M_color = _M_black;
}
inline _Rb_tree_node_base*
_Rb_tree_rebalance_for_erase(_Rb_tree_node_base* z,
_Rb_tree_node_base*& root,
_Rb_tree_node_base*& leftmost,
_Rb_tree_node_base*& rightmost)
{
_Rb_tree_node_base* y = z;
_Rb_tree_node_base* x = 0;
_Rb_tree_node_base* x_parent = 0;
if (y->_M_left == 0) // z has at most one non-null child. y == z.
x = y->_M_right; // x might be null.
else
if (y->_M_right == 0) // z has exactly one non-null child. y == z.
x = y->_M_left; // x is not null.
else
{
// z has two non-null children. Set y to
y = y->_M_right; // z's successor. x might be null.
while (y->_M_left != 0)
y = y->_M_left;
x = y->_M_right;
}
if (y != z)
{
// relink y in place of z. y is z's successor
z->_M_left->_M_parent = y;
y->_M_left = z->_M_left;
if (y != z->_M_right)
{
x_parent = y->_M_parent;
if (x) x->_M_parent = y->_M_parent;
y->_M_parent->_M_left = x; // y must be a child of _M_left
y->_M_right = z->_M_right;
z->_M_right->_M_parent = y;
}
else
x_parent = y;
if (root == z)
root = y;
else if (z->_M_parent->_M_left == z)
z->_M_parent->_M_left = y;
else
z->_M_parent->_M_right = y;
y->_M_parent = z->_M_parent;
std::swap(y->_M_color, z->_M_color);
y = z;
// y now points to node to be actually deleted
}
else
{ // y == z
x_parent = y->_M_parent;
if (x)
x->_M_parent = y->_M_parent;
if (root == z)
root = x;
else
if (z->_M_parent->_M_left == z)
z->_M_parent->_M_left = x;
else
z->_M_parent->_M_right = x;
if (leftmost == z)
if (z->_M_right == 0) // z->_M_left must be null also
leftmost = z->_M_parent;
// makes leftmost == _M_header if z == root
else
leftmost = _Rb_tree_node_base::_S_minimum(x);
if (rightmost == z)
if (z->_M_left == 0) // z->_M_right must be null also
rightmost = z->_M_parent;
// makes rightmost == _M_header if z == root
else // x == z->_M_left
rightmost = _Rb_tree_node_base::_S_maximum(x);
}
if (y->_M_color != _M_red)
{
while (x != root && (x == 0 || x->_M_color == _M_black))
if (x == x_parent->_M_left)
{
_Rb_tree_node_base* w = x_parent->_M_right;
if (w->_M_color == _M_red)
{
w->_M_color = _M_black;
x_parent->_M_color = _M_red;
_Rb_tree_rotate_left(x_parent, root);
w = x_parent->_M_right;
}
if ((w->_M_left == 0 ||
w->_M_left->_M_color == _M_black) &&
(w->_M_right == 0 ||
w->_M_right->_M_color == _M_black))
{
w->_M_color = _M_red;
x = x_parent;
x_parent = x_parent->_M_parent;
}
else
{
if (w->_M_right == 0
|| w->_M_right->_M_color == _M_black)
{
w->_M_left->_M_color = _M_black;
w->_M_color = _M_red;
_Rb_tree_rotate_right(w, root);
w = x_parent->_M_right;
}
w->_M_color = x_parent->_M_color;
x_parent->_M_color = _M_black;
if (w->_M_right)
w->_M_right->_M_color = _M_black;
_Rb_tree_rotate_left(x_parent, root);
break;
}
}
else
{
// same as above, with _M_right <-> _M_left.
_Rb_tree_node_base* w = x_parent->_M_left;
if (w->_M_color == _M_red)
{
w->_M_color = _M_black;
x_parent->_M_color = _M_red;
_Rb_tree_rotate_right(x_parent, root);
w = x_parent->_M_left;
}
if ((w->_M_right == 0 ||
w->_M_right->_M_color == _M_black) &&
(w->_M_left == 0 ||
w->_M_left->_M_color == _M_black))
{
w->_M_color = _M_red;
x = x_parent;
x_parent = x_parent->_M_parent;
}
else
{
if (w->_M_left == 0 || w->_M_left->_M_color == _M_black)
{
w->_M_right->_M_color = _M_black;
w->_M_color = _M_red;
_Rb_tree_rotate_left(w, root);
w = x_parent->_M_left;
}
w->_M_color = x_parent->_M_color;
x_parent->_M_color = _M_black;
if (w->_M_left)
w->_M_left->_M_color = _M_black;
_Rb_tree_rotate_right(x_parent, root);
break;
}
}
if (x) x->_M_color = _M_black;
}
return y;
}
参考:
1、C++ STL开发导引
2、SGI文件,MSDN