计数排序详解以及java实现

前言

我们知道，通过比较两个数大小来进行排序的算法（比如插入排序，合并排序，以及上文提到的快速排序等）的时间复杂度至少是Θ(nlgn)，这是因为比较排序对应的决策树的高度至少是Θ(nlgn)，所以排序最坏情况肯定是Θ(nlgn)。那有没有哪种排序算法的时间复杂度是线性的(Θ(n))呢？（因为我们如果要对一个数组排序，肯定至少要考察每个元素，因此可以推断Θ(n)是所有排序算法的下界）。答案是：在一定条件下，是有的。

思考过程

为了更好的理解计数排序，我们先来想象一下如果一个数组里所有元素都是整数，而且都在0-k以内。那对于数组里每个元素来说，如果我能知道数组里有多少项小于或等于该元素。我就能准确地给出该元素在排序后的数组的位置。

 

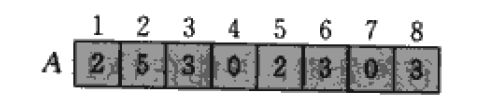
拿上图这个数组来说，元素5之前有8个元素小于等于5（含5本身），因此我排序后5所在的位置肯定是8.所以我只要构造一个（k+1）大小的数组，里面存下所有对应A中每个元素之前的元素个数，理论上就能在线性时间内完成排序。

算法过程

根据以上说明，我们能得出计数算法的过程：

1. 初始化一个大小为（k+1）的数组C（所有元素初始值为0），遍历整个待排序数组A，将A中每个元素对应C中的元素大小+1。操作结果见下图：

我们可以得到原数组中有2个0,0个1,2个2,3个3,0个4,1个5.

2.我们将C中每个i位置的元素大小改成C数组前i项和（基于之前的算法思考，我们不难理解这么做的道理）：

 

3.OK，现在我们已经快看到成功的曙光了。现在要做的就是初始化一个和A同样大小的数组B用于存储排序后数组，然后倒序遍历A中元素（后面会提到为何要倒序遍历），通过查找C数组，将该元素放置到B中相应的位置，同时将C中对应的元素大小-1（表明已经放置了一个这样大小的元素，下次再放同样大小的元素，就要往前挤一个位置）。遍历完A数组后，就完成了所有的排序工作（只画出了前3步）：

最后排序结果B:

我们现在回过头来思考一下为什么要限定A中是整数而且要限定元素大小？以及这个计数算法的时间复杂度是多少？

首先第一个问题，要知道我们要在C数组中存储所有A中对应元素之前的元素个数，因此如果不是整数或者大小范围无限大的话，我们就没法构造C数组，加之我们要对C数组遍历操作，如果K太大的话，这个算法的线性复杂度也就没有任何意义了。所以限制是整数纯粹只是为了限制C数组的大小，如果你想提出另外一种有限范围的限制，比如都是整数或者0.5结尾的小数（1.5,3.5等）也是可以的，只要将C的数组大小变成2k+2就可以了，只不过这种假设几乎没有任何实际意义而已。

对于第二个问题，我们来看看算法过程：第一步我们遍历了A数组，因此操作时间是Θ(n)，第二步遍历C数组操作时间是Θ(k)，第三步遍历A数组插入B，因此操作时间是也是Θ(n)。加起来时间复杂度就是Θ(n+k)。据此我们也能得到该算法的适用场景仅限于k较小的情况，如果k很大的话，就不如使用比较排序效率高了。

细心的读者应该还记得我在前文提过要解释为何要倒序遍历A数组，我们观察一下A数组中的3，我们可以看到有3个元素都等于3,对应位置:3,6,8。这3个3最后在5，6，7位置

我们是把8位置的3放在了7位置上，6位置的3放在了6位置上，3位置的3放在了5位置上。也就是说所有元素仍保持了之前的相对位置，我们称这个性质为排序的稳定性。有可能有人会觉得这个稳定性看起来没什么用，单纯从计数排序结果看，确实没什么用处，但是当在其他地方用到计数排序时，稳定性就非常有用了，比如我们在下一篇博客将要谈到的基数排序。

最后附上计数排序的java代码：

package sort;

public class CountSort {



    private static int[] countSort(int[] array,int k)

    {

        int[] C=new int[k+1];//构造C数组

        int length=array.length,sum=0;//获取A数组大小用于构造B数组  

        int[] B=new int[length];//构造B数组

        for(int i=0;i<length;i++)

        {

            C[array[i]]+=1;// 统计A中各元素个数，存入C数组

        }

        for(int i=0;i<k+1;i++)//修改C数组

        {

            sum+=C[i];

            C[i]=sum;    

        }

        for(int i=length-1;i>=0;i--)//遍历A数组，构造B数组

        {

            

            B[C[array[i]]-1]=array[i];//将A中该元素放到排序后数组B中指定的位置

            C[array[i]]--;//将C中该元素-1，方便存放下一个同样大小的元素

            

        }

        return B;//将排序好的数组返回，完成排序

        

    }

    public static void main(String[] args)

    {

        int[] A=new int[]{2,5,3,0,2,3,0,3};

        int[] B=countSort(A, 5);

        for(int i=0;i<A.length;i++)

        {

            System.out.println((i+1)+"th:"+B[i]);

        }

    }

}

 排序结果：