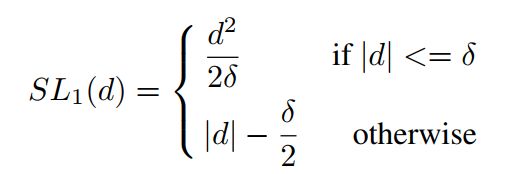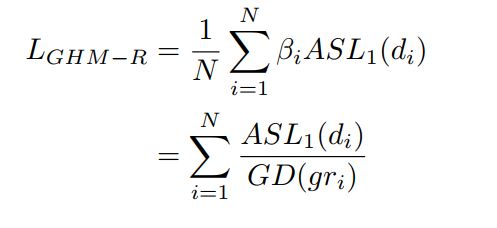- 作者要解决的问题
- Focal loss(CVPR2017)
- Focal loss的解决方案
- Focal loss的不足
- 设计思路
- 梯度与样本的关系
- 梯度模计算方法
- 改进
- GHM-C损失函数
作者要解决的问题
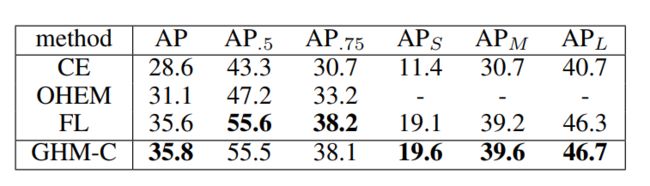
仍然是one-stage中的一个经典问题,正负、难易样本不均衡。因为anchor的原因,pos : neg>= 1 : 70。负样本大多比较简单,所以也导致了难易样本的问题。
Focal loss(CVPR2017)
Focal loss的解决方案
传统的交叉熵损失函数:
\(p^*=\{0, 1\}\)为真实标签,\(p \in (0, 1)\)为网络的预测概率。可以看到,传统的交叉熵损失函数平等的看待正负样本。
Focal loss
可以看到Focal loss引入了两个超参数\(\alpha, \gamma\),\(\alpha\)用来平衡正负样本,\(\gamma\)用来平衡难易样本。简单分析一下,加号的左侧是正样本的损失,右侧是负样本的损失。通过乘上不同的系数\((\alpha, 1-\alpha)\),来平衡正负样本。对于简单样本,其loss较小,概率值更接近真实标签,这样概率的\(\gamma\)次方越小,相反地,难样本的就会变大,使难样本的损失上升,使网络关注难样本。
Focal loss的不足
虽然Focal loss这篇论文也在一定程度上解决了正负样本不均衡的问题,但是Focal loss引入了两个超参数,调参费劲,且只能应用到box分类上,无法解决回归的问题。
设计思路
梯度与样本的关系
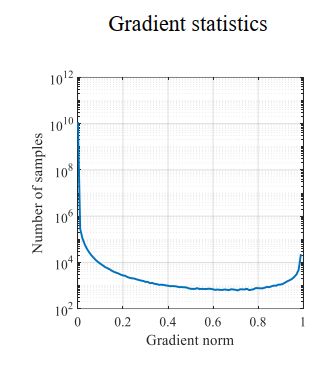
作者观察到难易样本的分布与梯度有着如下的关系,可以看到,梯度较小时(简单样本),样本数量非常多,梯度适中时,样本较少。另外值得注意的一点是,梯度在1左右的样本数量还是不少的。作者将这些样本视为异常值,解决特别难的样本会导致其他的样本准确率下降。
针对以上发现,作者采用梯度分布(梯度附近的样本数)来处理难易样本不平衡的问题。简单思路就是梯度小的样本数比较大,那就给他们乘上一个小系数,梯度大的样本少乘以一个大的系数。不过这个系数不是靠自己调的,而是根据样本的梯度分布来确定的。 ### 梯度分布计算方法:将0-1的梯度切bin,计算每个bin内落入的样本数量。 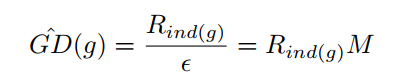 其中$\epsilon$是每个bin的宽度,$M$是$\epsilon$的倒数,表示将0-1切分成多少个bin,$R_{ind(g)}$表示每个bin内落入的样本数,计算方法如下:\(g\)是某点的梯度模,可以理解为以这一点创建一个bin,\(g_k\)是样本的梯度模,N是样本总数。
从上面式子可以看到,梯度分布越大,系数越小。
梯度模计算方法
具体的在二分类中,损失函数为上面提到的交叉熵函数
对x的梯度
定义梯度模\(g = |p-p^*|\)
改进
GHM-C损失函数
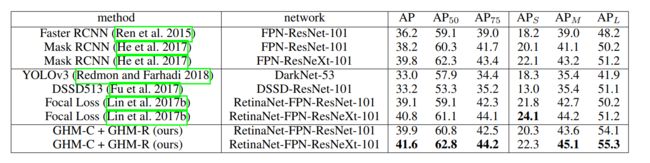
由此,作者提出分类的损失函数GHM-C