title: DALS015-Linear Models线性模型04方差分析
date: 2019-08-20 12:0:00
type: "tags"
tags:
- ANOVA
- 线性模型
categories: - 生物统计
前言
这一部分是《Data Analysis for the life sciences》的第5章线性模型的第4小节,这一部分的主要内容涉及ANOVA,有关方差分析的笔记R markdown文档可以参考作者的Github。
ANOVA简介
现在考虑一种情况,如果我们想知道push与pull的差值在整体上,不同的组中是否有区别。换句话讲,我们并不想比较任意两组有差异,我们就想知道,在所有的有腿中,代表了push和pull差值的3个交互作用导致的push和pull差异是否比正常的差异大(即不考虑交互作用的情况)。
通过方差分析(analysis of variance,ANOVA)就可以解决这个问题。ANOVA的本质在于比较不同复杂模型的残差平方和是被哪些因素降低的(我的理解就是,总的残差平方和都是分布在哪些变量上面,哪些变量分到的最多,哪些变量的效应就最强)。含有8个系数的模型比含有5个系数的模型要复杂的多,在5个系数的模型中,我们是假设push和pull在所有组之间的差异是相等的。最简单的模型只使用一个系数,一个截矩。在某些假设下,我们还可以执行推断,确定与我们观察到的一样大的改进概率(Under certain assumptions we can also perform inference that determines the probability of improvements as large as what we observed)。
下面的ANOVA计算的结果(接前文案例):
> anova(fitX)
Analysis of Variance Table
Response: friction
Df Sum Sq Mean Sq F value Pr(>F)
type 1 42.783 42.783 1179.713 < 2.2e-16 ***
leg 3 2.921 0.974 26.847 2.972e-15 ***
type:leg 3 2.098 0.699 19.282 2.256e-11 ***
Residuals 274 9.937 0.036
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
结果的第一行中有一个type变量(表示pull或push),它对应的Sum值为42.783,这就表示,这一单一的系数减少了42.783的平方和。我们看一下总的平方和,其实就是线性模型的截矩,也可以是anova(fitX)的第2列的和,如下所示:
result <- anova(fitX)
sum(result$`Sum Sq`)
mu0 <- mean(spider$friction)
(initial.ss <- sum((spider$friction - mu0)^2))
结果如下所示:
> result <- anova(fitX)
> sum(result$`Sum Sq`)
[1] 57.73858
> mu0 <- mean(spider$friction)
> (initial.ss <- sum((spider$friction - mu0)^2))
[1] 57.73858
需要注意是的是,这个平方和的计算公式最初就是来源于样本方差的计算公式,如下所示:
N <- nrow(spider)
(N - 1) * var(spider$friction)
计算结果如下所示:
> N <- nrow(spider)
> (N - 1) * var(spider$friction)
[1] 57.73858
现在来看一下,前面的42.783是如何得到的。我们需要计算仅包含类型信息模型的残差平方和。我们可以通过计算残差,残差的平方,并将它们加起来就能实现,如下所示:
s <- split(spider$friction, spider$type)
after.type.ss <- sum( sapply(s, function(x) {
residual <- x - mean(x)
sum(residual^2)
}) )
(type.ss <- initial.ss - after.type.ss)
结果如下所示:
> s <- split(spider$friction, spider$type)
> after.type.ss <- sum( sapply(s, function(x) {
+ residual <- x - mean(x)
+ sum(residual^2)
+ }) )
> (type.ss <- initial.ss - after.type.ss)
[1] 42.78307
这个降低的程度(就是上面的42.78307)就相当于模型~type和~1拟合值差值的平方和,如下所示:
sum(sapply(s, length) * (sapply(s, mean) - mu0)^2)
结果如下所示:
> sum(sapply(s, length) * (sapply(s, mean) - mu0)^2)
[1] 42.78307
线性模型中的各个项的顺序以及ANOVA表格中的顺序很重要:每行表示的是:当添加了一个新的系数后,残差平方和较未添加这个系数之前减少的量。
在ANOVA表(这个表其实就是ANOAVA计算后的结果)还标明了自由度。当引入了type这一项时,它对应的Df就是1,leg变量引入了3个项(即legL2,legL3和legL4),它对应的Df就是3(这一段不太理解)。ANOVA还有一列是F value。F值表示的是包含感兴趣的项(感兴趣的项平方和除以相应自由度)除以残差(ANOVA表中的最后一行除以自自由度),以第一行为例 说明一下就是(42.783/1)/(9.937/274)=1179.686。
书中给出的公式为:
其中p表示模型中系数的总数(在这个模型中,包括截矩在内的系数总数是8)。
在零假设成立的前提下(零假设就是添加系数的真值为0),我们会得到每行F值分布的理论结果。这种近似所需的假设类似于t分布近似的假设,例如我们在使用CLT时需要大量的样本,或者是总体的数据服从正态分布。
现在我们来解释一下p值,看最后一行,即type:leg,内容是type:leg 3 2.098 0.699 19.282 2.256e-11 ***,type:leg表示的是3个交互作用系数。在零假设下,这3个附加项的真实值为0,例如,,,,然后我们就计算出ANOVA表的这一行观察到的这么大的F值的概率。这里需要记住,我们只关注大的F值,因为我们有一个平方和的比,因此F值只能是正数(原文:Remember that we are only concerned with large values here, because we have a ratio of sum of squares, the F-value can only be positive. )。type:leg这一行中的p值可以这么解释:在零假设下,我们认为push和pull的差值在所有组之间是没有差异的,p值表示了,在这个零假设成立时,我们观察到的如此大的方差的可能性。从计算结果中我们可以看到,我们的p值非常小,我们就可以拒绝零假设,即可以认为,push和pull的差值在不同组之间是不同的。
另外,ANOVA中的F值与F分布有关,F分布有2个以参数,一个是分子的自由度(分子是研究对象的自由度,例如前面提到的交互作用),一个是分母的自由度(残差)。从结果可以看到,交互作用系数的自由度是3,残差的自由度是274。
ANOVA模型的另外表示
现在来看一下ANOVA模型的另外表示方法,在这种方式里,我们假设每一对type与leg都有自己的均值(这样,对于每一条腿来说,push与pull的效应就不会相同)。这种表述方式在某种程度上来说更加简单,但是,我们不能像前面那样构建ANOVA表,因为这种方式无法区分交互作用系数。
首先我们会先构建一个因子变量,这个因子变量表示的是type与leg的组合,在公式中含有~0,它表示,我们不在线性模型中包含截矩,其中我们通过rafalib包中的imagemat()函数绘制了组变量的矩阵示意图,这个示意图也有8项,它针对每一个type和leg组合进行了拟合,代码如下所示:
##earlier, we defined the 'group' column:
spider$group <- factor(paste0(spider$leg, spider$type))
X <- model.matrix(~ 0 + group, data=spider)
colnames(X)
head(X)
library(rafalib)
imagemat(X, main="Model matrix for linear model with group variable")
fitG <- lm(friction ~ 0 + group, data=spider)
summary(fitG)
coefs <- coef(fitG)
coefs
结果如下所示:
> colnames(X)
[1] "groupL1pull" "groupL1push" "groupL2pull" "groupL2push" "groupL3pull"
[6] "groupL3push" "groupL4pull" "groupL4push"
> head(X)
groupL1pull groupL1push groupL2pull groupL2push groupL3pull groupL3push
1 1 0 0 0 0 0
2 1 0 0 0 0 0
3 1 0 0 0 0 0
4 1 0 0 0 0 0
5 1 0 0 0 0 0
6 1 0 0 0 0 0
groupL4pull groupL4push
1 0 0
2 0 0
3 0 0
4 0 0
5 0 0
6 0 0
> library(rafalib)
> imagemat(X, main="Model matrix for linear model with group variable")
> fitG <- lm(friction ~ 0 + group, data=spider)
> summary(fitG)
Call:
lm(formula = friction ~ 0 + group, data = spider)
Residuals:
Min 1Q Median 3Q Max
-0.46385 -0.10735 -0.01111 0.07848 0.76853
Coefficients:
Estimate Std. Error t value Pr(>|t|)
groupL1pull 0.92147 0.03266 28.21 <2e-16 ***
groupL1push 0.40735 0.03266 12.47 <2e-16 ***
groupL2pull 1.14533 0.04917 23.29 <2e-16 ***
groupL2push 0.52733 0.04917 10.72 <2e-16 ***
groupL3pull 1.27385 0.02641 48.24 <2e-16 ***
groupL3push 0.37596 0.02641 14.24 <2e-16 ***
groupL4pull 1.40075 0.03011 46.52 <2e-16 ***
groupL4push 0.49075 0.03011 16.30 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1904 on 274 degrees of freedom
Multiple R-squared: 0.96, Adjusted R-squared: 0.9588
F-statistic: 821 on 8 and 274 DF, p-value: < 2.2e-16
> coefs <- coef(fitG)
> coefs
groupL1pull groupL1push groupL2pull groupL2push groupL3pull groupL3push groupL4pull
0.9214706 0.4073529 1.1453333 0.5273333 1.2738462 0.3759615 1.4007500
groupL4push
0.4907500
计算估计系数
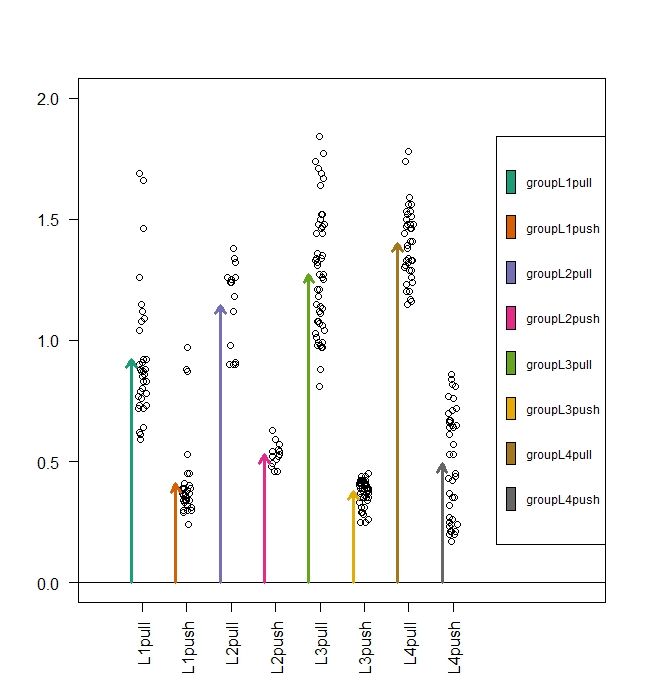
现在我们绘制出上面计算结果的示意图,如下所示:
stripchart(split(spider$friction, spider$group),
vertical=TRUE, pch=1, method="jitter", las=2, xlim=c(0,11), ylim=c(0,2))
cols <- brewer.pal(8,"Dark2")
abline(h=0)
for (i in 1:8) {
arrows(i+a,0,i+a,coefs[i],lwd=3,col=cols[i],length=lgth)
}
legend("right",names(coefs),fill=cols,cex=.75,bg="white")
使用contrast包进行简单比较
虽然无法使用这个公式来进行ANOVA分析,但是可以使用contrast()函数对每组的估计系数进行比较,如下所示:
groupL2push.vs.pull <- contrast(fitG,
list(group = "L2push"),
list(group = "L2pull"))
groupL2push.vs.pull
coefs[4] - coefs[3]
结果如下所示:
> groupL2push.vs.pull
lm model parameter contrast
Contrast S.E. Lower Upper t df Pr(>|t|)
1 -0.618 0.0695372 -0.7548951 -0.4811049 -8.89 274 0
> coefs[4] - coefs[3]
groupL2push
-0.618
无截矩时差值的差异
我们还可以进行push和pull在各级之间的两两(pair-wise)比较。例如,现在我们想比较L3与L2的push和pull的差值,如下所示:
其过程如下所示:
C <- matrix(c(0,0,1,-1,-1,1,0,0), 1)
groupL3vsL2interaction <- glht(fitG, linfct=C)
summary(groupL3vsL2interaction)
names(coefs)
(coefs[6] - coefs[5]) - (coefs[4] - coefs[3])
结果如下所示:
> C <- matrix(c(0,0,1,-1,-1,1,0,0), 1)
> groupL3vsL2interaction <- glht(fitG, linfct=C)
> summary(groupL3vsL2interaction)
Simultaneous Tests for General Linear Hypotheses
Fit: lm(formula = friction ~ 0 + group, data = spider)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
1 == 0 -0.27988 0.07893 -3.546 0.00046 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported -- single-step method)
> names(coefs)
[1] "groupL1pull" "groupL1push" "groupL2pull" "groupL2push" "groupL3pull"
[6] "groupL3push" "groupL4pull" "groupL4push"
> (coefs[6] - coefs[5]) - (coefs[4] - coefs[3])
groupL3push
-0.2798846
练习
P230