lucas求大组合数

Lucas 定理

Lucas 定理用于求解大组合数取模的问题，其中 p 必须为素数。正常的组合数运算可以通过递推公式求解，但当问题规模很大，而模数是一个不大的质数的时候，就不能简单地通过递推求解来得到答案，需要用到 Lucas 定理。

---

代码实现

long long Lucas(long long n, long long m, long long p) {
     
  if (m == 0) return 1;
  return (C(n % p, m % p, p) * Lucas(n / p, m / p, p)) % p;
}

例题

Chessboard（icpc 2019 nanjing B）

Sunday morning has come, and all the autumn would be bright and cool, and brimming with life.There was a song in every heart,and if the heart was young the music issued at the lips.There was cheer in every face and a whoop in every step.Tom appeared on the sidewalk with a bucket of whitewash and a long-handled brush.He surveyed the stone chessboard in the park, and all gladness left him and a deep melancholy settled down upon his spirit.A giant chessboard, that is nn feet long and mm feet wide.Life to him seemed hollow, and existence but a burden.

Sighing, he dipped his brush with a little whitewash and thought how to start. He knew that he would select a starting point, which should be an arbitrary block in the chessboard. He would whitewash the block and move to an adjacent one; repeat the operation and finish his work in any place when the whole chessboard has been whitewashed. His footprints would defile a painted region even if he took off his shoes. So avoiding to go back to a completed block would be a wise choice.

But Tom’s energy did not last. He began to think of the fun he had planned for this day, and his sorrows multiplied. Soon the free boys and girls would come tripping along the Yan Lake inside Nanjing University of Aeronautics and Astronautics Jiangning campus, and they would have the chance to take part in the ICPC contest facing interesting algorithms problems. Staring at the chessboard, a sudden curiosity urged him to pay attention to, between any two painted blocks, the shortest paths only passing painted blocks in which adjacent blocks should share a common edge.

“Damn it! The shortest distances may vary. I have to stop such a thing happening.”

He quickly imagined a strategy that the shortest distance between any two blocks would remain unchanged after they were painted, and it would be a satisfactory beginning:

and another strategy not to be considered:

Now he wants to know how many different satisfactory strategies are there that can whitewash the whole chessboard.Can you help him?

Input
The first line contains an integer T~(1\le T\le 10^5)T (1≤T≤10 ^5 ) indicating the number of test cases.

For each test case, a single line containing two integers nn and m~(1\le n, m\le 10^6)m (1≤n,m≤10 ^6
) describes the size of the chessboard.

Output
For each test case, output the number of different satisfactory strategies modulo (10^9+7)(1e9+7).

样例输入

4
1 3
3 2
3 3
4 4

样例输出

2
12
24
80

---

如果当前被染色的区域是个 r ( r ≥ 2 ) 行 c ( c ≥ 2 ) 列的矩形，那么接下来要么扩充成r+1 行 c列的矩阵(扩充行)，要么扩充成 r行 c + 1列的矩形(扩充列)。并且根据当前状态中最后一个被染色的格子在哪个角上，扩充行/列的方案都是唯一的。

从 1 ∗ 1 的矩阵，到 n ∗ m 的矩阵，一共要扩充n+m-2
次，其中有 n − 1次是扩充行，这样的决策有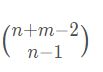

种，根据最后一个被染色的格子在哪个角上，方案数为

Corner case: n = 1 或者m=1，小心特判掉即可。

#include 
using namespace std;
typedef long long ll;
const int N=1e6+10,mod=1e9+7;

ll fact[N],infact[N];

ll qmi(ll a,ll k,ll p)//快速幂
{
     
    ll res=1;
    while(k)
    {
     
        if(k&1) res=(ll)res*a%p;
        k>>=1;
        a=(ll)a*a%p;
    }
    return res;
}
ll C(ll a,ll b,ll mod)//小费马求组合数
{
     
	return (ll)fact[a]*infact[b]%mod*infact[a-b]%mod;
}
ll lucas(ll n,ll m,ll p)//卢卡斯定理
{
     
	if(m==0) return 1;
	return (C(n%p,m%p,p)*lucas(n/p,m/p,p)%p);
}
int main()
{
     
    fact[0]=1,infact[0]=1;
    for(int i=1; i<N; i++)//预处理
    {
     
        fact[i]=(ll)fact[i-1]*i%mod;
        infact[i]=(ll)infact[i-1]*qmi(i,mod-2,mod)%mod;
    }

    int t;
    cin>>t;
    while(t--)
    {
     
        ll n,m;
        ll ans=0;
        cin>>n>>m;
        if(n==1||m==1) ans=2;
        else {
     
        	ans=4*lucas(n+m-2,n-1,mod);
		}
		ans=ans%mod;
        cout<<ans<<endl;
    }
    return 0;
}