力扣——174.地下城游戏(困难难度)——万能的递归与动态分析

一、算法目录合集

1.地址

   算法目录合集

2.说明

  该地址指向所有由本人自己所经历的算法习题(也有可能仅仅是一个入门的案例或者是经典案例)，仅仅为我做过而且比较有意思的，也许还会有一些我自己想出来的，出于兴趣写在这里,具体格式我会在下面列明，总目录也会在这里出现，方便查阅以及自己进行复习回顾。

二、题目说明

1.题干

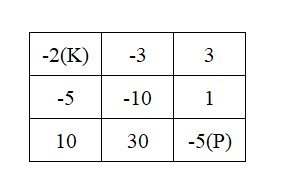
  一些恶魔抓住了公主（P）并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士（K）最初被安置在左上角的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

  骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

  有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

  为了尽快到达公主，骑士决定每次只向右或向下移动一步。

  编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。

  例如，考虑到如下布局的地下城，如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下，则骑士的初始健康点数至少为 7。

  说明:

• 骑士的健康点数没有上限。
• 任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

2.原地址

  174. 地下城游戏

三、实现步骤

1.思路分析

1.1.分析问题

  对于这个题,有一种常规的方法——动态分析（一看这不就是动态分析），因为血量是由两个条件决定的（每个房间不能死掉，并且到终点时血量最少），所以正着去分析时有难度，不如讲血量定为1，反向分析，也就是说：当我们到达坐标$(i,j)$时，如果此时我们的路径和不小于 $dp[i][j]$ ，我们就能到达终点。 既然要反向分析了，那我就不展示动态分析了，动态分析官方题解也有，我就用一个一提反向就能想起来的词儿去做：递归。没错，我已经在前几篇文章讲过递归的一些题了，这其实也可以递归求解。

  首先要分析一下，如何递归？
  关注一下上面一段的黄线，就假设前面已经操作完了，那么现在我们只需要选取向右或者向下，取一个$min$就可以了，直接调用$Math.min()$方法就行了，如果这时候我们的现存血量减去本格子的耗血量（负值也适用）大于零，就说明或者，那么便可以让血量变成1（既然多少血都能或者，那么1可以使血量保持最低），如果小于零，说明之前的血量不够用，那么剩余血量必须得是最小值$min$减去本格的耗血量。

  就这样一直递归回第一步，返回即可。

1.2.具体步骤

① 特殊情况分析

  如果遇到了边界，则返回int的最大值过滤，之所以不写999或者9999，是因为你也不知道一个格子究竟扣多少血，万一给你来个几万呢所以来个Integer.MAX_VALUE稳妥一些。

if (m >= dungeon.length || n >= dungeon[0].length) {
     
	return Integer.MAX_VALUE;
}

  如果找到了公主，则返回所就到公主之前的时候的血量最小值，把值返回，以供调用者使用。

if (m == dungeon.length - 1 && n == dungeon[0].length - 1) {
     
	return dungeon[m][n] >= 0 ? 1 : 1 - dungeon[m][n];
}

  如果本位置为0，说明dp还没有被赋值，此项判断是为了把指针放在公主的位置，并往回寻找。

if (dp[m][n] != 0) {
     
	return dp[m][n];
}

② 常规分析

  常规步骤就是比较简单的了，选取两种分支的最小值，并将其与本格子的耗血量进行比较，来为dp数组赋值储存，最终返回$dp[0][0]$即可。

int min = Math.min(blood(dp,dungeon, m + 1, n), blood(dp,dungeon, m, n + 1));
dp[m][n] = dungeon[m][n] - min >= 0 ? 1 : min - dungeon[m][n];
return dp[m][n];

2.代码实现

2.1 方法代码

public class Solution174 {
     
    public int calculateMinimumHP(int[][] dungeon) {
     
        int[][] dp = new int[dungeon.length][dungeon[0].length];
        return blood(dp, dungeon, 0, 0);
    }

    public int blood(int[][] dp, int[][] dungeon, int m, int n) {
     
        if (m >= dungeon.length || n >= dungeon[0].length) {
     
            return Integer.MAX_VALUE;
        }
        if (m == dungeon.length - 1 && n == dungeon[0].length - 1) {
     
            return dungeon[m][n] >= 0 ? 1 : 1 - dungeon[m][n];
        }
        if (dp[m][n] != 0) {
     
            return dp[m][n];
        }
        int min = Math.min(blood(dp,dungeon, m + 1, n), blood(dp,dungeon, m, n + 1));
        dp[m][n] = dungeon[m][n] - min >= 0 ? 1 : min - dungeon[m][n];
        return dp[m][n];
    }
}

2.2 测试部分代码

  这里随便定义一个随便看看就好了

public class Test174Hard {
     
    public static void main(String[] args) {
     
        Solution174 s = new Solution174();
        int i1 = s.calculateMinimumHP(new int[][]{
     {
     1, 2, 3}, {
     0, -5, 0}, {
     -2, 1, 1}});
        int i2 = s.calculateMinimumHP(new int[][]{
     {
     -2,-3,3},{
     -5,-10,1},{
     10,30,-5}});
        System.out.println(i1);
        System.out.println(i2);
    }
}

  测试结果

1
7

2.3 耗用资源情况

四、官方题解

1.原地址

力扣官方答疑戳这里

2.方法一——动态规划

思路分析

思路及算法
  几个要素：「$M\times N$ 的网格」「每次只能向右或者向下移动一步」。让人很容易想到该题使用动态规划的方法。
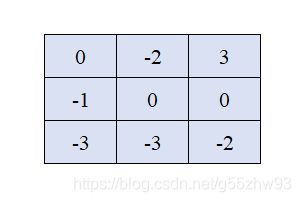
  但是我们发现，如果按照从左上往右下的顺序进行动态规划，对于每一条路径，我们需要同时记录两个值。第一个是「从出发点到当前点的路径和」，第二个是「从出发点到当前点所需的最小初始值」。而这两个值的重要程度相同，参看下面的示例：

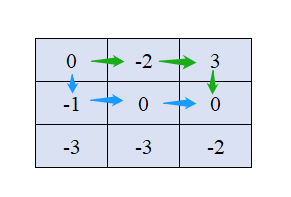
  从$(0,0)$到$(1,2)$ 有多条路径，我们取其中最有代表性的两条：

• 绿色路径「从出发点到当前点的路径和」为 $1$，「从出发点到当前点所需的最小初始值」为 $3$。
• 蓝色路径「从出发点到当前点的路径和」为 $-1$，「从出发点到当前点所需的最小初始值」为 $2$。

  
  我们希望「从出发点到当前点的路径和」尽可能大，而「从出发点到当前点所需的最小初始值」尽可能小。这两条路径各有优劣。
  在上图中，我们知道应该选取绿色路径，因为蓝色路径的路径和太小，使得蓝色路径需要增大初始值到 $4$ 才能走到终点，而绿色路径只要 $3$ 点初始值就可以直接走到终点。但是如果把终点的$-2$ 换为 $0$，蓝色路径只需要初始值 $2$，绿色路径仍然需要初始值 $3$，最优决策就变成蓝色路径了。
  因此，如果按照从左上往右下的顺序进行动态规划，我们无法直接确定到达 $(1,2)$ 的方案，因为有两个重要程度相同的参数同时影响后续的决策。也就是说，这样的动态规划是不满足「无后效性」的。
  于是我们考虑从右下往左上进行动态规划。令 $dp[i][j]$ 表示从坐标$(i,j)$ 到终点所需的最小初始值。换句话说，当我们到达坐标$(i,j)$时，如果此时我们的路径和不小于 $dp[i][j]$ ，我们就能到达终点。
  这样一来，我们就无需担心路径和的问题，只需要关注最小初始值。对于 $dp[i][j]$ ，我们只要关心 $dp[i][j+1]$ 和 $dp[i+1][j]$ 的最小值$minn$。记当前格子的值为$dungeon(i,j)$，那么在坐标 $(i,j)$ 的初始值只要达到$minn-dungeon(i,j)$ 即可。同时，初始值还必须大于等于 $1$。这样我们就可以得到状态转移方程：
  
$$dp[i][j]=max(min(dp[i+1][j],dp[i][j+1])-dungeon(i,j),1)$$
  最终答案即为 $dp[0][0]$。
  边界条件为，当 $i=n-1$ 或者$j=m-1$ 时，$dp[i][j]$ 转移需要用到的$dp[i][j+1]$ 和 $dp[i+1][j]$ 中有无效值，因此代码实现中给无效值赋值为极大值。特别地，$dp[n-1][m-1]$ 转移需要用到的 $dp[n-1][m]$ 和 $dp[n][m-1]$ 均为无效值，因此我们给这两个值赋值为 $1$。

代码实现（Java）

class Solution {
     
    public int calculateMinimumHP(int[][] dungeon) {
     
        int n = dungeon.length, m = dungeon[0].length;
        int[][] dp = new int[n + 1][m + 1];
        for (int i = 0; i <= n; ++i) {
     
            Arrays.fill(dp[i], Integer.MAX_VALUE);
        }
        dp[n][m - 1] = dp[n - 1][m] = 1;
        for (int i = n - 1; i >= 0; --i) {
     
            for (int j = m - 1; j >= 0; --j) {
     
                int minn = Math.min(dp[i + 1][j], dp[i][j + 1]);
                dp[i][j] = Math.max(minn - dungeon[i][j], 1);
            }
        }
        return dp[0][0];
    }
}

复杂度

• 时间复杂度：
     $O(N\times M)$，其中$N$，$M$ 为给定矩阵的长宽。
• 空间复杂度：
    $O(N\times M)$，其中$N$,$M$ 为给定矩阵的长宽，注意这里可以利用滚动数组进行优化，优化后空间复杂度可以达到 $O(N)$。