【超详细】区块链技术基础知识梳理与比特币介绍

区块链基础知识梳理（1）

写在前面

         笔者查询、借鉴了一些资料，看过不少介绍区块链的文章，发现很多文章虽然写得不错，但不或多或少会不太适合小白初步了解区块链和比特币的相关原理，本文旨在通过对比特币相关机制的介绍，详细说明区块链的原理和基础内容。当然，笔者也是刚刚接触区块链不久，难免会有一些错误的理解，还望读者斧正。全文共计7500字，通过提问和举例的方式详细地介绍了比特币和区块链的相关机制，希望能给大家带来帮助。

 

引入：（比特币）

         有个与世隔绝的村子，村子里没有流通的纸币，大家通过记账的方式进行交易。一开始村民进行交易的时候都会把这笔交易记录下来，当做凭证，村子里的每个人都会在账目上记录村子中每条交易信息。但这么一来，每个人的账本上都会有除了自己的交易信息以外的大量其他与自己无关的交易信息，同时大家也不太愿意花费自己的时间精力和存储空间记录他人的账目。为了减轻大家的工作量，大家决定暂且由村长担任记账先生对村子里产生的每一笔交易信息进行记录，按照日期每天生成一个账本，每个账本都记录着当天内产生的交易的相关信息。村长记录后每天定时定点公布账单，供大家核对和检查。村民们核对无误以后，每个人都会将当日的账本抄一份自己保留。

        显然，这很像中心化的管理，类似于我们银行的操作模式。

（1）然而，新的问题来了，村长一直花时间和精力给大家记账，没有收益怎么办？

         村民们想了个好办法，在每次产生交易的过程中，需要为此次交易支付一定的手续费（假设为1元），这个手续费将给予村里的记账人。

 

（2）随着村子的发展，村子的日交易数量逐渐变多，记账人的收益越来越多，其他人发现记账有利可图，认为一直让一个人记账不公平，也想参与记账工作，那要怎么选取记账人呢？

         为了公平地选取记账人，村民们每天早上掷骰子，根据点数决定谁来记当天的账，其他人只要核对一下，没问题就抄写下来。此处村民们选取记账人的规则就称为“共识机制”，确保每个人都有参与记账的机会。同时，村子里每天会产生一个账单，每天的账单其实就是一个区块，区块中记录着当天的交易信息，而每天的账单末尾会记录当天每个村民的交易结余（即每个人还剩多少钱），前一天的交易结余在新一天的账本中将会作为当日的交易数额（即你有多少钱），通过前一天的交易结余和当天的交易数额以及相邻的日期等关系就可以串联起各个账单（区块），即为“链”。

 

（3）如果这时候有人想要挪用村里的公款，虽然他不用直接篡改账本上的信息（因为大家都会确认账本上的信息），但是可以烧掉账本中的一部分内容，这样别人就查不出来了，回头只要告诉大家这是不小心碰到蜡烛，别人也没什么办法。如何防止这种事情的发生？

         是每个人都拥有一本自己的账本，任何一个人改动了账本都必须要告知所有其他人，其他人会在自己的账本上同样地记上一笔，如果有人发现新改动的账目不对，可以拒绝接受，到了最后，以大多数人都一致的账目表示为准。所以即便是有人真的不小心损坏了一部分账本的内容，只要找到其他的人去重新复制一份来就行了。

 

（4）有些村民离账本公布的地点比较远或者当天没时间去核对账本该怎么办？

        相邻的村民可以互相抄写当天的账本（即邻居之间相互抄写账本），也叫做区块链的路由。此处的村民的相互抄写可以看作是点对点交流，而村民可以看作一个普通节点。

       通过上述描述，我们可以知道区块链有以下特点：

      1.难以篡改   2.P2P   3.每个节点都有打包的权利（共识机制） 4.去中心化

 

进一步说明：

         更进一步说明区块链。首先以比特币举例，假设有A、B、C、D四个节点，每个节点都会在账本上记录四个节点间发生的交易的相关信息。

        同理，会引出以下问题：

    （1）为什么每个节点都要记账？

       因为记账有奖励。每笔交易需要缴纳手续费（比银行低得多），同时每次记账打包的人，都会获得一定的比特币奖励（打包奖励）。

         2018年，中本聪在一开始发明这个机制的时候，设定的是每10分钟产生一次区块，即会每十分钟会选取一个记账人，并将这10分钟产生的交易内手续费和50个比特币用于奖励打包的人（记账人）。奖励的打包费（50个比特币每四年减少一半，即到2012年以后打包费变为25比特币，2016年以后打包费变为12.5，以此类推，总计会产生2100万个比特币作为打包费。在打包费无限接近0以后，将通过收取手续费奖励打包人）

 

  （2）这么多节点都记录了账单，以谁的账单为准？

         这就涉及我们之前所说的记账人选取机制，即“共识机制”，只不过此处的共识机制会比较复杂。在比特币中，各个节点需要通过做“数学题”的方式争夺记账权，即为Pow（工作量证明的方式）我们将做题的过程称为挖矿，谁先做出这道“数学题”，谁就有权利记账，同时我们把挖矿的人叫做矿工。

    “数学题”原理：

         此处的“数学题”需要用到哈希函数的知识。以哈希函数中的SHA256为例说明，我们可以将任何字符串（小到几kb的字符串，大到10G的电影）输入SHA256函数中，其输出结果为唯一的256位的二进制序列（比如输入为LR即SHA（LR），其输出即为10001000.....等32位数的唯一的二进制数，当稍微改变输入值，输入位LR1即（LR1），其输出将会有很大变动，即稍微改变输入的值，将会使得输出值有巨大变化）

      哈希函数正向计算容易，反向计算困难，即为单向函数。举个例子，对于下面的函数： 

                                                        

        知道X未知数，求Y很容易，但知道Y，要求X就很困难。实际上哈希函数还要比所举例子复杂得多（感兴趣可以去看看密码学相关资料了解具体操作过程，此处仅需知道无论大小如何的字符串输入至哈希函数以后，输出会得到独一无二的长度固定的二进制字符串）

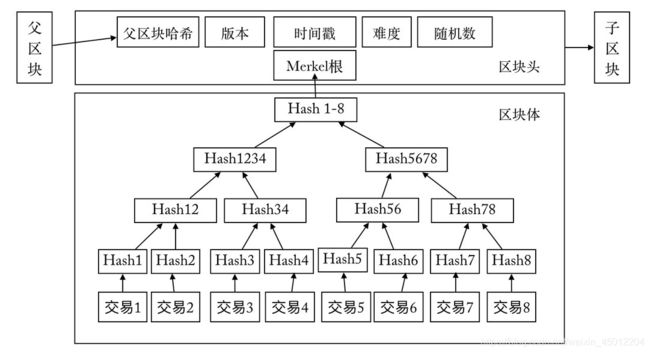
        回到我们之前说的数学题，首先我们得了解区块的结构，如图所示，区块包括区块头和区块体，此处暂且不需要理会区块体内的具体内容，我们先看到区块头，我们的数学题很大一部分来自于区块头。

区块结构体

         此处的数学题为每个节点有一个字符串，字符串内容为：

字符串=前一个区块的块头+账单（默克尔根）+时间戳+……(此处仅列举一部分)+随机数

        数学题要求输入为SHA256(SHA256(字符串))，输出结果为前n位为0的二进制数（序列），即 

 Hash=SHA256(SHA256(字符串))=前n位为0的二进制序列

         由字符串的组成可知，仅有随机数可以改变，其他部分的内容都是确定的，而因为哈希函数的单向性，很难从输出结果推算出输入结果，因此仅能通过改变随机数的数值，逐个暴力计算（盲猜），使输出满足所需条件。虽然不同的节点的时间戳、默克尔根（账单）等信息可能不同，但总的来说，计算能力越强，也有能力算出所需的二进制序列。

         此外，可以通过调整难度，即改变n的值以此确保每10分钟内必定会产生一个区块，比特币一开始设置的n=66，当然会随着矿机数量的增多（单位时间内运算总数增多）而适当调高题目难度，保证在指定时间内能产生区块。

 

（3）如何防伪？（如何证明某个交易信息说由某个人发起的，某条转账新的付款人是A而不是B，如何确保交易信息不被伪造）

         传统的方式身份认证方式是以签字（看字迹），指纹，瞳孔（独一无二的生物特征）等方式进行身份认证。然而，在互联网中，这些都可以直接进行复制伪造，此时我们需要引入“数字签名”的概念。

         而在计算机世界中，保证数字签名不被伪造是通过数字摘要和非对称加密实现的，举个比特币中交易的例子:假如现在A发起一笔比特币转账，需要先将该交易进行数字摘要，缩短成一段字符串，然后用自己的私钥对摘要进行加密，形成数字签名。完成后，需要将交易信息（包括收款方的地址）和数字签名一起广播给记录“账本的人”也就是矿工。矿工用A的公钥进行验证，如果验证成功，说明该笔交易确实是A发出的，且信息未被更改，是完整的。

         此处涉及数字签名需要运用到数字摘要和非对称加密的知识，现在逐一介绍：

        数字摘要

         技术用于对所要传输的数据进行运算生成信息摘要，它并不是一种加密机制，但却能产生信息的数字”指纹”，它的目的是确保数据没有被修改或变化，保证信息的完整性不被破坏。说直白点就是将数据进行hash编码。它在数字签名中的作用就是增加被伪造的难度，就好比有些人故意把字要写的龙凤凤舞，目的就是很难让他人伪造。

 

         在介绍非对称加密前需要首先介绍对称加密。

        对称加密

         举个例子：现在A（未成年）想跟他的朋友B想聊一个比较敏感的话题，但是他怕他的老妈会翻看他的手机，要是让她知道自己跟别人聊这种话题肯定会挨骂，于是A就和朋友B约定好A将中文先翻译成英文再发过去，然后他那边可以使用微信翻译将英文翻译成中文，这样即使老妈看到了也无所谓，因为她根本看不懂英语，于是A跟他的朋友B便聊了起来，当A将中文通过翻译软件转换成英文后，发给B，他的朋友B再利用翻译软件将英文转化为中文即可正常读取你发送的信息即如图所示：

A与B信息传递过程（对称加密）

         如图所示，无论加密（A将中文信息翻译成英文）还是解谜（B将英文信息翻译成中文）都运用到了翻译工具（即一方通过密钥将信息加密以后，把密文传给另一方，另一方通过这个相同的密钥对密文进行解密）

         对称加密是比较好理解的，将一个密钥通过加密算法对明文进行运算得到一个密文，使用同样的密钥作为解密算法的输入对密文进行解密即可得到原文，如下图所示：

                             

对称加密示意图

         从这里我们可以看出对称加密有几个要素，分别是明文、加密算法、密钥、密文以及解密算法，明文即原始数据，密钥与明文一起作为加密算法的输入，是将明文进行打乱的规则，当然它也是跟密文一起作为解密算法的输入。密文自然就是加密算法得到的结果。

         但这么做有缺陷，如果A的老妈使用了微信翻译将发送出去的英文翻译成中文她不就看懂了吗?对的，这就是对称加密的缺陷，一旦被人拿到了密钥（在对称加密中，密钥就是加解密的规则），那么A发送出去的密文将轻而易举被人破解，那么有什么方法做到即使一个人的密钥被盗窃了，最起码保证A发给其他人发送密文不被破解？就是说即使A的老妈获取到了你的密钥，但她仍然无法破解你发送出去的信息，只有他的朋友B才能查看A发送给他的信息。这个就是我们要讲的非对称加密。

 

        非对称加密

        在非对称加密中，不管是信息的发送方还是信息的接收方都有一对属于自己的公钥和密钥，公钥顾名思义就是可以公开，而私钥就是只能自己看，不能给别人拿到。接着发送方会将信息进行数字摘要并使用接收方的公钥进行加密，然后再使用自己的私钥对数字摘要进行加密，接收方收到加密后的信息跟加密串，用 发送方的公钥（因为公钥是公开的）来解密加密串，得到原始的数字摘要，然后对使用自己的私钥进行解密的信息进行摘要后的结果进行比对。如果一致，说明该文件确实是该发送方发过来的，并且文件内容没有被修改过。

 

     非对称加密如何运用到身份认证中呢？

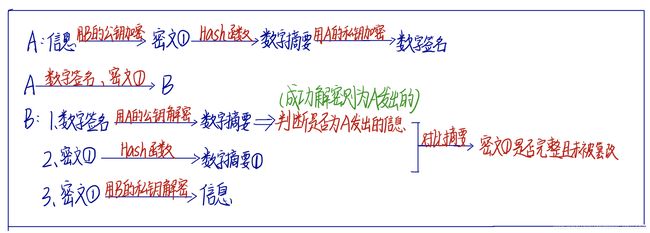
         还是以A给B发信息为例：A使用他的朋友B的公钥对你的信息进行加密，并且对信息进行数字摘要，然后使用A自己的私钥对摘要进行加密，即数字签名，然后将数字签名和加密后的信息一起发送给B，B接收到信息后，先使用A的公钥对数字签名进行解密，证明该信息确实是A发送过来的而不是别人发送过来的（因为可以成功用A的公钥解密，所以可以说明是A发来的信息），然后再使用自己的私钥（B的私钥）对加密后的信息进行解密（注意这里只有B的私钥才能解密信息，其他人都不可以，即使是A本人也不能解密，所以就算是A的老妈拿到了A的私钥也没办法破解该信息），然后对该信息使用同样的算法进行数字摘要，如果得到的摘要跟A发送过来的摘要一致，则说明信息在传递的过程中没有被修改过。（详情如图）

身份认证过程

 

       回到区块链的防伪：

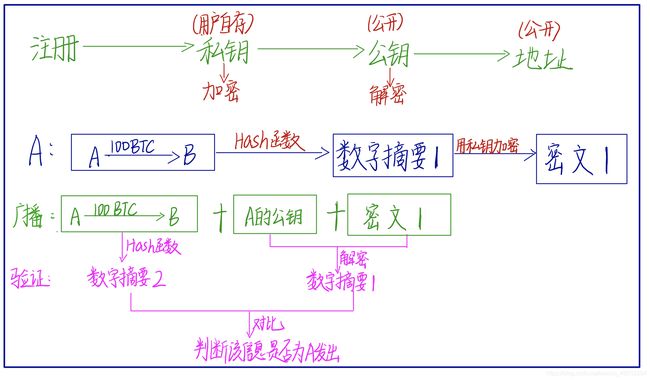
         还是以A要给B发信息为例，此处A要给B转100个BTC（比特币），首先A先将此条交易进行哈希运算处理得到一穿256位的二进制序列，此处称为数字摘要1，之后再利用A的私钥对数字摘要1进行加密，称为密文1。之后将加密以后的密文1以及A的公钥、A给B转100个BTC的信息广播于其他节点，其他节点收到信息后，使用A的公钥对密文1进行解密，得到数字摘要1，同时对“A给B转100个BTC”这条信息进行哈希运算，得到数字摘要2，对比数字摘要1和数字摘要2，如果两个数字摘要完全相同，即可说明此条信息是A发出的，“A给B转100个BTC”这条信息真实完整且未被篡改。（详情如图）

区块链中的身份认证

 

         此时我们已经做到了防伪造，那么如何防止双重支付呢？

（双重支付：即坏人拿一份钱当两分钱使用，即A只有10个BTC，但A同一时间向全网广播向C和B分别转了10个BTC，因为网络延时，其他的节点收到这两条信息的时间可能不同，我们该如何防止不同节点确认了不同的交易信息而产生双重支付问题呢？）

     此处首先要说明比特币的交易过程：

    1.付款人签署交易单

         付款人需要输入自己的比特币地址以及收款方的比特币地址，还要输入转账比特币的个数，如5个比特币，然后付款方会发送一个请求给收款方（以P2P的形式发送），在发送这个请求之前付款人会先加上收款人的公钥和交易信息，然后再用自己的私钥加密整个请求，并把自己的公钥标记在这个请求上。这里需要注意的是付款人不仅要将这个请求发给收款方，还需要以P2P的方式广播出去告诉其他网络节点，让所有节点都接收到这个请求。 举个例子Alice要给Bob转账5个比特币，那么Alice首先要询问Bob的标识字符串（比特币地址），例如是“ABCDEFG”，同时Alice也有一个标识字符串例如是“HIJKLMN”，然后Alice写一张单子，内容为“HILKLMN支付5比特币给ABCDEFG”，然后用自己的保密印章（私钥）盖一个章，将这张单子交给Bob。

    2.收款人确认单据签署人

         收款人收到这个请求后拿着付款人的公钥进行解密，如果能解密则说明付款人确实是拥有这个私钥的，进而说明这笔账是从付款人转过来的，还可以得到收款人的公钥（因为上面已经讲了付款人会将收款人的公钥跟交易信息进行加密）说明这笔账确实是转给收款人的。

    3.确认付款人余额

         通过上面的步骤是可以确定这笔账确实是付款人发起的，但是没办法有效的确认付款人是否真的有足够的余额进行转账（毕竟现在没有一个中心机构进行认证），所以这个时候就需要矿工来进行确认，这是因为在比特币的世界里是没有余额这个概念的，我们在比特币钱包里看到的“余额”不是我们所理解的余额，它其实是UTXO（意思是未花费的交易输出，这个打算在第五篇讲），验证付款方是否有余额这个工作通常由矿工来做，而收款方不需要做这个工作，只需要验证这个请求是否是付款人发起的即可。

 

   PS：如何检查余额？

         实际上，区块链在创立的过程中，交易信息被大多数节点接收且成功打包到公链后才可确认交易信息（即确认账款到账）。在交易过程中，比如A要给B转10个BTC，其他节点会到公链上的区块中查找有关A的交易信息，并计算出A的“余额”，如果余额大于等于转账值，即接受该交易信息，反之拒绝该交易信息。我们把余额检查的过程叫做“追溯”。交易信息被其他节点拒绝即无法被记入各个节点的账本中，那么就没法被打包加入区块中。

         A同时向其他节点广播向B和C分别转账了10BTC的时候（假设A只有10BTC），这两条交易信息可能会因为网络延时被记录到两个不同的节点中，但这些节点只有一个节点可以打包记账，因此一旦一个节点获得记账权被打包记账，那么剩下的节点的区块则会被丢弃，即接受了另一条交易信息的区块则被丢弃，因此只有一条交易信息会被确认，同时A的余额会被修改（即可A剩余BTC为0），则交易池中的另一个交易信息会因余额不足而不能被节点接收。

 

    （4）如何防止篡改？

         按照之前所说的，我们已经了解了如何防止篡改，即无法伪造他人的交易信息，但还有一个问题，怎么防止坏人修改（删减）自己之前在某一区块的交易信息呢？

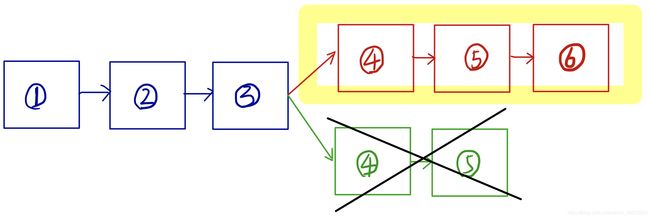
         首先引入最长链原则，正如前文所说的，矿工们通过挖矿的方式争取记账权，如果出现两个矿工同时挖出一个符合条件的区块的情况（称为分叉），该如何处理呢？

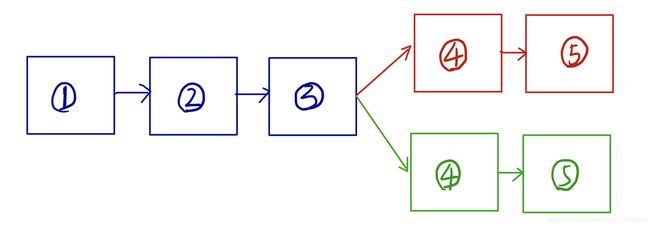
       在某一时刻有两个矿工同时算出随机数（即获得记账权），那么这个时候便会出现一种情况，即一条主链叉开变成两条叉链，每条链沿着各自的方向延伸下去，如下图所示：

分叉示意图1

         之所以会出现这种情况是因为每个矿工在开始挖新的区块之前都会先把上一个区块复制过来，然后接上这个区块进行下一个区块的挖矿工作。而现在在全网中的同一时刻有两个符合条件的区块，同时算出这道“数学题”的两个矿工会向全网广播自己解出了题目，那么由于距离的远近（P2P网络，可以理解成有延时），矿工找到的区块是不一样的（虽然这两个区块都是符合条件的区块，但他们可能因为距离解出结点的大小不同而接收到不同的区块），所以有一些矿工会拿到红色的区块进行下面的挖矿工作，而有一些矿工会拿到绿色的区块进行挖矿工作，这就势必导致上图所示的情况，这种情况叫分叉。

         比特币则设定了一种机制，即短链服从长链。首先区块是由矿工挖出来的，矿工进行挖矿就需要矿机（显卡），而不同的矿机具有不同的算力（每秒运算多少次），也就是说每个矿工的计算能力是不一样的，那么，就会出现一种情况，即两条链中会有一条链的算力要比另一条链大，因此这条链的增长速度就会比另一条链要快，也就是这条链会比另一条链长。这时你可能会说那如果两条链的算力一直保持一样呢？这种情况是不可能会出现的，在短时间内是可能的，但一段时间后这种平衡势必会被打破，比如有新的矿机出来（新的矿机算力一般都比较高），那么就会有矿工去购买来替换旧的矿机，这就会导致算力不平衡。

        但其中一条链超过另外一条链时，这时全网中就会出现一条最长链，那么矿工在进行新的打包区块工作的时候会把最长链全部复制过来，再在这条链的基础上继续挖矿，当所有矿工都这样做的时候那么这条链就会成为一条主链，而另外一条链就会被抛弃掉，如下图所示，红链将会成为主链（公链），而绿色的链将会被废弃，重新被放入交易池中，等待打包。

分叉示意图2

 

         其实可以想成“加赛”，如果两个矿工同一时间挖到矿，其身边的节点因为网络的延时会对挖出来的区块进行站队，站队后继续挖矿，谁能挖出下一个矿使得该链上的区块更多（使得该链更长），就以谁的链为准，当其他矿工发现有比自己所在的链还要长的链以后，就会放弃自己现在所在的链，转而到较长链上站队，一般而言，6个区块内即可分出胜负（即可比较出哪条链较长，以哪条链为准）。

         如果矿工执意要在那条短链上进行挖矿呢？如果这个矿工聪明一点的话他就知道这么做是吃力不讨好的，因为一旦他所在的链最后没有成为主链的话，他在这条连上挖到的比特币都会归零，他之前所做的工作都白费的，所以一般不会去做这种事。

         所以，如何篡改交易信息呢？

        如果有个矿工要篡改信息，他需要拥有比其他所以矿工更多CPU算力（51%攻击），那么，这个51%攻击是什么实现的？

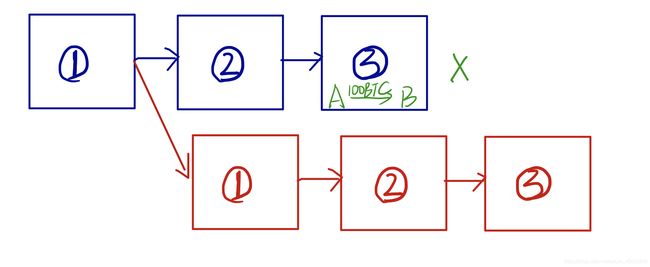
假设一个场景，A用100比特币向B购买一样商品，步骤如下：

       （1）A支付给B 100BTC；

      （2）B收到100BTC确认收款后发货（一般认为6次确认后交易就不可逆转）；

      （3）A随即创建另一笔交易，将同样的10BTC支付给自己。

     

51%攻击（篡改交易信息）

       如图所示，A想要撤销第一笔交易，不用花钱就得到B的商品。为了达到这个目的，A进行了双重支付，将同样的100BTC支付给B和自己。在正常的比特币网络中，一旦第一笔交易经过6次确认后就几乎不可更改，后续的交易数据将继续打包成新的区块依次链接下去。可是，如果A用户拥有51%的算力，情况将会发生有趣的变化，A可以实现双重支付的目的。即该矿工需要拥有比其他人更多的算力，在现有的链条上，打包出比现有主链更长的分叉，让全网公认自己的链条是主链。

        51%攻击能带来的收益是非常有限的，只能做到：

1、修改自己的交易记录，如双重支付 2、阻止确认部分或全部交易

       而下面这些即使是51%攻击也没法做到的：

1、凭空生成比特币； 2、修改每个区块产生的比特币数量。

       然而，当该矿工掌握了全网51%的算力，他将被迫进行选择，是通过欺诈以偷回其支付的款项（即双花攻击），还是通过（获取）生成的新货币。他应当会发现，按照规则行事更加有利可图，这样的规则有利于他比其他联合起来的每一个人获取更多的新货币，亦优于破坏系统以及损害自己拥有财富的有效性。

 

写在最后

      有关区块链的知识还有很多，包括共识机制、智能合约、简单支付验证（SPV）等内容，之后会逐一补充，如有疑问，欢迎交流。

参考资料：

（1）https://blog.csdn.net/weixin_37504041/article/details/92798560

（2）https://blog.csdn.net/weixin_37504041/article/details/79872329

（3）https://zhuanlan.zhihu.com/p/96314968

（4）https://blog.csdn.net/weixin_37504041/article/details/80070410