【数据结构Python描述】自底向上构建二叉堆实现及其O(n)时间复杂度分析

在文章【数据结构Python描述】树堆（heap）简介和Python手工实现及使用树堆实现优先级队列中，为了能对优先级队列中键值对的增删都较为高效，我们基于二叉堆实现了HeapPriorityQueue。

对于使用HeapPriorityQueue创建的对象q，其中用于保存优先级队列键值对的二叉堆初始为空，如后续需要通过优先级队列操作的键值对数量为$n$，虽然我们大可以重复调用$n$次对象q的add(k, v)方法来构建堆，但是根据文章【常见算法Python描述】优先级队列应用之实现选择排序、插入排序和堆排序的分析，该操作的最坏时间复杂度为$nlog(n)$。

如果$n$对键值对提前给定，如【常见算法Python描述】优先级队列应用之实现选择排序、插入排序和堆排序中具有$n$个元素的待排序集合，此时就可通过本文下面将介绍的自底向上（Bottom-Up）方式构建二叉堆，这种方式的最坏时间复杂度为$O(n)$。

一、堆数据结构创建

为描述方便，下面介绍自底向上构建堆的方式时，假设给定数量为$n=2^{h+1}-1$（其中$h$为堆的高度）的任意顺序键值对，则数量为$n$的键值对恰好可以填满高度为$h$的完全二叉树，且每一层的键值对数量分别为$1$、$2^1$、$2^2$、$\cdot \cdot \cdot$、$2^{h-1}$、$2^h$，此时二叉树的高度为$h=log(n+1)-1$。

1. 建堆步骤

下面以给定$n=15$个键值对为例介绍如何自底向上构建堆：

易知，上述$n=15$个键值对可以填满高度为$h=log(16)-1=3$的完全二叉树（但根据堆的定义，此时完全二叉树还不是堆），如下图(a)所示：

下面的图(b)至图(h)介绍了具体的建堆过程：

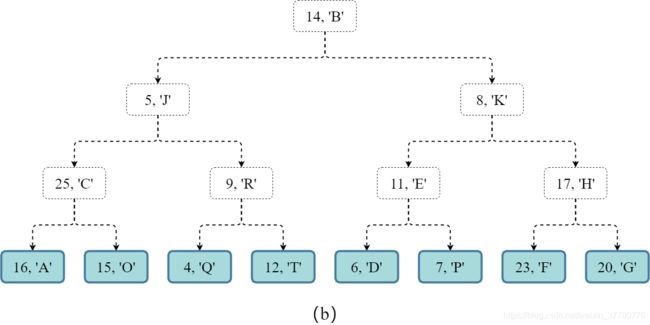
• 第一步（如图(b)所示），构建$(15+1)/2^1=8$个仅有一个键值对的堆：

• 第二步：
  • 首先如图(c)所示，构建$(15+1)/2^2=4$个完全二叉树，每个包含$3$个键值对；
  • 然后如图(d)所示，因为每个完全二叉树都可能违背堆序性质，因此可能需要进行父子结点间键值对的交换，最后才能得到$4$个堆。

• 第三步：
  • 首先如图(e)所示，构建$(15+1)/2^3=2$个完全二叉树，每个包含$7$个键值对；
  • 然后如图(f)所示，因为每个完全二叉树都可能违背堆序性质，因此可能需要进行父子结点间键值对的交换，最后才能得到$2$个堆。

• 第四步：
  • 首先如图(g)所示，构建$(15+1)/2^4=1$个完全二叉树，其中包含$15$个键值对；
  • 然后如图(h)所示，因为该完全二叉树都可能违背堆序性质，因此可能需要进行父子结点间键值对的交换，最后才能得到根据给定的$15$个键值对需构建的$1$个二叉堆。

2. 建堆实现

分析上述建堆过程可知，实现建堆最重要的是如何将两个形态和大小完全相同的子堆在根结点处进行合并，且保证合并后得到的完全二叉树是一个二叉堆。

实际上，对于以列表方式给出键值对形式结点元素的完全二叉树，文章【数据结构Python描述】树堆（heap）简介和Python手工实现及使用树堆实现优先级队列中介绍的自堆顶向下冒泡算法实现_downheap()恰好可以满足该需求。

具体地，在实现上述建堆过程时，只需要对完全二叉树从最底层最右侧结点开始直到根结点的每一个结点使用一个循环，依次调用_downheap()方法即可。

更进一步地，因为_downheap()方法不对叶子结点执行任何操作，所以上述循环只需从最底层的非叶子结点开始依次调用_downheap()方法。

对上述分析使用Python实现如下：

def __init__(self, contents=tuple()):
    """
    初始化一个优先级队列
    默认将新创建的优先级队列初始化为空，如果提前给定元素为(k, v)形式的contents集合，则使用contents初始化优先级队列
    :param contents:(k, v)形式元素contents集合
    """
    self._data = [self._Item(k, v) for k, v in contents]
    if len(self._data) > 1:
        self._heapify()

def _heapify(self):
    """
    具体执行自底向上建堆
    :return: None
    """
    start = self._parent(len(self) - 1)  # 从最后一个叶子结点的父结点开始
    for j in range(start, -1, -1):  # 自底向上
        self._downheap(j)

分析上述代码可知，建堆实现只是将HeapPriorityQueue的__init__()方法进行了重新设计并提供了一个非公有的实用方法_heapify()，其逻辑为：在使用HeapPriorityQueue创建对象时，其初始化方法接收一个可选参数contents，该参数是元素为(k, v)形式的元组，与旧的初始化方法不同的是，这里使用列表推导式初始化后续建堆用的列表。

3. 建堆效率

为了分析自底向上建堆的实现_heapify()方法的时间复杂度，这里：

• 首先给出结论：

针对提前给定的$n$个键值对，如采用自底向上的方式构建堆，则假定键值对间两两比较的时间复杂度为$O(1)$，则该建堆方式的最坏时间复杂度为$O(n)$。

• 然后以上述给定的$15$个键值对为例进行验证；
• 最后再进行一般性分析。

对于给定具有任意顺序的$15$个键值对：

在_heapify()中，最坏情况下，循环每一次迭代的运行时间正比于当前结点到最底层结点（此处为第$4$层结点）的高度，因此：

• 第$4$层结点数量为$2^3=8$，但是_heapify()不对这些结点执行任何操作，因此本层的时间复杂度为$0$；
• 第$3$层结点数量为$2^2=4$，当前所有结点到最底层结点（此处为第$4$层结点）的高度为$1$，则对该层每个结点调用_downheap()的最坏时间复杂度正比于$4\times 1=4$；
• 第$2$层结点数量为$2^1=2$，当前所有结点到最底层结点（此处为第$4$层结点）的高度为$2$，则对该层每个结点调用_downheap()的最坏时间复杂度正比于$2\times 2=4$；
• 第$1$层结点数量为$2^0=1$，当前所有结点到最底层结点（此处为第$4$层结点）的高度为$3$，则对该层每个结点调用_downheap()的最坏时间复杂度正比于$1\times 3=3$。

综上，即_heapify()的最坏时间复杂度正比于$4+4+3=11<15$。

一般地，对于给定具有任意顺序的$n=2^{h+1}-1$个键值对：

• 第$h$层结点数量为$2^h$，但是_heapify()不对这些结点执行任何操作，因此本层的时间复杂度为$0$；
• 第$h-1$层结点数量为$2^{h-1}$，当前所有结点到的高度为$1$，则对该层每个结点调用_downheap()的最坏时间复杂度正比于$2^{h-1}\times 1$；
• 第$h-2$层结点数量为$2^{h-2}$，当前所有结点到的高度为$2$，则对该层每个结点调用_downheap()的最坏时间复杂度正比于$2^{h-2}\times 2$；
• $\cdot \cdot \cdot \cdot \cdot \cdot$
• 第$h-j$层结点数量为$2^{h-j}$，当前所有结点到的高度为$j$，则对该层每个结点调用_downheap()的最坏时间复杂度正比于$2^{h-j}\times j$；
• $\cdot \cdot \cdot \cdot \cdot \cdot$
• 第$0$层结点数量为$2^0$，当前所有结点到的高度为$h$，则对该层每个结点调用_downheap()的最坏时间复杂度正比于$2^0\times h$。

因此，总的建堆时间复杂度正比于：

$$f(n)={\sum }_{j=0}^{h}j{2}^{h-j}$$

变形后得：

$$f(n)=2^h{\sum }_{j=0}^h\frac{j}{2^j}$$

因此，重点是求下列表达式的和：

$${\sum }_{j=0}^h\frac{j}{2^j}$$

为了求出上述表达式的和，需要使用下面的数学技巧：

• 首先，根据高中数学知识，对任意$x<1$，有下列等比数列求和公式：

$${\sum }_{j=0}^{\infty }{x}^j=\frac{1}{1-x}$$

• 然后，上述等式两端对$x$求导后得：

$${\sum }_{j=0}^{\infty }j{x}^{j-1}=\frac{1}{(1-x{)}^2}$$

上式两边同乘以$x$后得：

$${\sum }_{j=0}^{\infty }j{x}^j=\frac{x}{(1-x{)}^2}$$

• 最后，如果令上述等式$x=1/2$，则：

$${\sum }_{j=0}^{\infty }\frac{j}{2^j}=\frac{1/2}{(1-(1/2){)}^2}=2$$

因此：

$$f(n)=2^h{\sum }_{j=0}^h\frac{j}{2^j}<2^h{\sum }_{j=0}^{\infty }\frac{j}{2^j}=2^h\times 2=2^{h+1}$$

又本节开头假定$n=2^{h+1}-1$，于是$f(n)<n+1\in O(n)$。至此，证毕。

二、完整测试代码

下面是针对【数据结构Python描述】树堆（heap）简介和Python手工实现及使用树堆实现优先级队列中实现的HeapPriorityQueue，使用自底向上建堆方法完善后得到的最终结果及其测试代码：

# heap_priority_queue.py
from priority_queue import PriorityQueueBase


class Empty(Exception):
    """尝试对空优先级队列进行删除操作时抛出的异常"""
    pass


class HeapPriorityQueue(PriorityQueueBase):
    """使用堆存储键值对形式记录的优先级队列"""

    def __init__(self, contents=tuple()):
        """
        初始化一个优先级队列
        默认将新创建的优先级队列初始化为空，如果提前给定元素为(k, v)形式的contents集合，则使用contents初始化优先级队列
        :param contents:(k, v)形式元素contents集合
        """
        self._data = [self._Item(k, v) for k, v in contents]
        if len(self._data) > 1:
            self._heapify()

    def _heapify(self):
        """
        具体执行自底向上建堆
        :return: None
        """
        start = self._parent(len(self) - 1)  # 从最后一个叶子结点的父结点开始
        for j in range(start, -1, -1):  # 自底向上
            self._downheap(j)

    def _parent(self, j):
        """
        返回父结点处业务元素在列表中的索引
        :param j: 任意结点处的业务元素在列表中的索引
        :return: 父结点处业务元素在列表中的索引
        """
        return (j - 1) // 2

    def _left(self, j):
        """
        返回左子结点处业务元素在列表中的索引
        :param j: 任意结点处的业务元素在列表中的索引
        :return: 左子结点处业务元素在列表中的索引
        """
        return 2 * j + 1

    def _right(self, j):
        """
        返回右子结点处业务元素在列表中的索引
        :param j: 任意结点处的业务元素在列表中的索引
        :return: 右子结点处业务元素在列表中的索引
        """
        return 2 * j + 2

    def _has_left(self, j):
        """
        如结点有左子结点则返回True，否则返回False
        :param j: 任意结点处的业务元素在列表中的索引
        :return: 判断结点是否有左子结点的Boolean结果
        """
        return self._left(j) < len(self._data)  # 确保列表索引不越界

    def _has_right(self, j):
        """
        如结点有右子结点则返回True，否则返回False
        :param j: 任意结点处的业务元素在列表中的索引
        :return: 判断结点是否有右子结点的Boolean结果
        """
        return self._right(j) < len(self._data)  # 确保列表索引不越界

    def _swap(self, i, j):
        """
        交换一对父子结点的业务元素
        :param i: 业务元素在列表中的索引
        :param j: 业务元素在列表中的索引
        :return: None
        """
        self._data[i], self._data[j] = self._data[j], self._data[i]

    def _upheap(self, j):
        """
        自堆底向上冒泡算法
        :param j: 结点处业务元素在列表中的索引
        :return: None
        """
        parent = self._parent(j)
        if j > 0 and self._data[j] < self._data[parent]:
            self._swap(j, parent)
            self._upheap(parent)  # 递归调用

    def _downheap(self, j):
        """
        自堆顶向下冒泡算法
        :param j: 结点处业务元素在列表中的索引
        :return: None
        """
        if self._has_left(j):
            left = self._left(j)
            small_child = left
            # 如果有左、右两个子结点，令small_child引用键较小子结点的业务元素在列表中的索引
            if self._has_right(j):
                right = self._right(j)
                if self._data[right] < self._data[left]:
                    small_child = right
            # 至少根结点有左子结点时，才有可能self虽然是完全二叉树但不是堆
            if self._data[small_child] < self._data[j]:
                self._swap(j, small_child)
                self._downheap(small_child)  # 递归调用

    def __len__(self):
        """返回优先级队列中的记录条目数"""
        return len(self._data)

    def __iter__(self):
        """生成优先级队列中所有记录的一个迭代"""
        for each in self._data:
            yield each

    def add(self, key, value):
        """向优先级队列中插入一条key-value记录"""
        self._data.append(self._Item(key, value))  # 新记录条目插入并确保完全二叉树性质
        self._upheap(len(self._data) - 1)  # 确保满足堆序性质

    def min(self):
        """返回（但不删除）优先级队列中键最小的记录，如优先级队列此时为空则抛出异常"""
        if self.is_empty():
            raise Empty('优先级队列为空！')
        item = self._data[0]
        return item.key, item.value

    def remove_min(self):
        """回并删除优先级队列中键最小的记录，如优先级队列此时为空则抛出异常"""
        if self.is_empty():
            raise Empty('优先级队列为空！')
        self._swap(0, len(self._data) - 1)  # 将根结点处键最小记录交换至完全二叉树最底层最右侧结点处
        item = self._data.pop()
        self._downheap(0)  # 确保完全二叉树满足堆序性质，即确定需保存在根结点处的键最小记录
        return item.key, item.value


if __name__ == '__main__':
    heap_queue = HeapPriorityQueue()
    print(heap_queue.is_empty())  # True

    heap_queue.add(4, 'C')
    heap_queue.add(6, 'Z')
    heap_queue.add(7, 'Q')
    heap_queue.add(5, 'A')
    print(heap_queue)  # [(4, 'C'), (5, 'A'), (7, 'Q'), (6, 'Z')]

    heap_queue.add(2, 'T')
    print(heap_queue)  # [(2, 'T'), (4, 'C'), (7, 'Q'), (6, 'Z'), (5, 'A')]

    print(heap_queue.remove_min())  # (2, 'T')
    print(heap_queue.remove_min())  # (4, 'C')
    print(heap_queue)  # [(5, 'A'), (6, 'Z'), (7, 'Q')]
    print(heap_queue.min())  # (5, 'A')
    print(heap_queue.is_empty())  # False

实际上，虽然我们在分析自底向上建堆方式时假设给定的价值对个数为$n=2^{h+1}-1$个，但实际上对于任意数量的键值对，上述实现的_heapify()方法均支持，具体留待读者思考。

三、参考资料

• [1] Lecture 14: HeapSort Analysis and Partitioning