BNU Concentric Rings
http://www.bnuoj.com/bnuoj/problem_show.php?pid=16030
Concentric Rings
There are several different concentric rings on the ground. Some of them may overlap. In Figure 1, there are 3 rings: blue, green and red. The red one is just above the green one. The problem is to remove minimum number of rings so that no two of the remaining overlap.
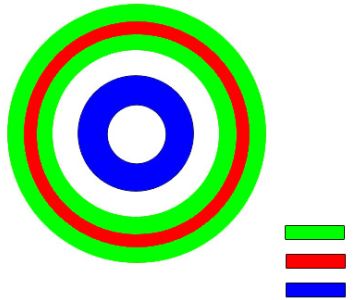
Figure 1
The input consists of multiple test cases. Each test case starts with a positive integer N (<=10000) which represents the number of rings. The next N lines each line contains two positive integers which represents the inner radius and outer radius respectively.
OutputFor each test case, output the minimum number of rings to remove.
Sample Input:3 1 2 3 6 4 5Sample Output:
1
Source
这题和杭电上有个看电视的那个一样,简单贪心题,这个题首先输入有n个环,接下来每行都是环的内半径和外半径,然后求满足不能有重叠所需要删除几个环。
AC代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
struct Node
{
int inner,outer;
}a[10010];
bool cmp(Node a, Node b)
{
return a.outer < b.outer;
}
int main()
{
int n,i,j,sum;
while(scanf("%d",&n)!=EOF)
{
sum = 0;
for(i = 0; i < n; i++)
{
scanf("%d%d",&a[i].inner,&a[i].outer);
}
sort(a,a+n,cmp);
j = 0;
for(i = 1; i < n; i++)
{
if(a[i].inner < a[j].outer)
{
sum++;
a[i].inner = a[i].outer = 0;
}
else
{
j = i;
}
}
printf("%d\n",sum);
}
return 0;
}