[翻译]AGG 之适应性细分法描画贝塞尔曲线（上）

Adaptive Subdivision of Bezier Curves

     -- An attempt to achieve perfect result in Bezier curve approximation

原文地址：http://www.antigrain.com/research/adaptive_bezier
/index.html#PAGE_ADAPTIVE_BEZIER

翻译：唐风

前言：这篇文章的翻译确实很拙劣，已经超出我的能力之外。计算机图形学里的用语，以及文中的一些算法的细节都没有很好的领会，翻译出来之后自己也非常不满意。但还是想先帖出来，毕竟已经花了一些功夫。后面我会根据自己进一步地理解修正这篇翻译中不正确的地方，也希望错误之处读者能指点出来。一般来说，如果您需要最为准确的信息，最好参照原文。另外，本文翻译的修正，可能只会在我的 cnblogs 上的博客上进行，其它博客上是否修正取决于精力是否足够，非常抱歉。

完成本文的翻译后，我会继续学习 AGG 的原代码，AGG 官方网上还有一篇关于字体渲染的文章也在我的计划之内，但为了不再出现这篇这样理解不清的翻译，我会推后一步，等我对 AGG 以及 2D 的计算机图形学有进一步的理解之后进行。

---

Introduction

贝塞尔曲线在现代的 2D 和 3D 描画中被广泛使用。在大多数的程序中，使用二次或是三次的曲线就足够了。在互联网上有大量的关于贝塞尔曲线的解释，我相信你看过之后就知道它是怎么回事了。现在，主要问题是我们如何（在计算机上）画出这种曲线。

曲线的描画通常都是使用一系列的短小的线段来近似的，这是描画曲线的唯一高效的方法。在这篇文章里，我要解释的是这样一种方法：如何通过使用最少的点来达到最完美的近似效果。

首先我们得先看一下 Paul Bourke 在下面这个链接中说明的一个基本方法：

http://astronomy.swin.edu.au/~pbourke/curves/bezier

下面的这段代码用来计算一条三次（贝塞尔）曲线上的任意一个点（这是从 Paul 的网页上拷下来的）

/*

Four control point Bezier interpolation

mu ranges from 0 to 1, start to end of curve

*/

XYZ Bezier4(XYZ p1,XYZ p2,XYZ p3,XYZ p4,double mu)

{

    double mum1,mum13,mu3;

    XYZ p; 

    mum1 = 1 - mu;

    mum13 = mum1 * mum1 * mum1;

    mu3 = mu * mu * mu; 

    p.x = mum13*p1.x + 3*mu*mum1*mum1*p2.x + 3*mu*mu*mum1*p3.x + mu3*p4.x;

    p.y = mum13*p1.y + 3*mu*mum1*mum1*p2.y + 3*mu*mu*mum1*p3.y + mu3*p4.y;

    p.z = mum13*p1.z + 3*mu*mum1*mum1*p2.z + 3*mu*mu*mum1*p3.z + mu3*p4.z; 

    return(p);

}

这里面，有四个控制点和一个叫 "mu" 的参数，mu 的取值范围是 [0,1] 。原则上这就足够了，我们可以使用递增的 mu 来计算出一系统的点，并用这些点来画面近似用的线段。

Problems of the Incremental method

首先，这个方法很慢，2D 的情况下，每个点的计算需要进行 24 次浮点数乖法。不过这个问题可以很容易的解决，我们可以使用递增的方法代替这种直接计算，在这篇文章的最后有相关的描述：Interpolation with Bezier Curves，你可以看到，主循环中只有 6 次加法操作。就我所知，这是目前最快的方法，特别是在现代的处理器上更是如此，因为这些处理器对浮点数的计算都已经相当的快了。

但主要的问题是如何决定中间点的数目，还有如何对 mu 值进行递增。最简单的方法是选择某个步进，比如，每次增加 0.01 ，这样任何曲线都会被分成 99 条线段。当然，缺点也显而易见，对于长曲线中间点太少，而对于短曲线中间点则太多。

很显然，我们应该基于曲线的长度来计算步进，但计算曲线长度又要求我们能计算出曲线本身，于是，在这里我们陷入了经典的“第二十二条军规”的尴尬矛盾中（译注：因为我们对曲线的长度和形状都是不确定的，所以用线段来近似它，但最佳的线段的数目和长度最要求我们知道曲线长度和形状）。（所以，为此，我们要找别的方法），对于长度，采用有一个相当不错的估算方法：

(p1,p2)+(p2,p3)+(p3,p4);

根据这个，我通过实验发现典型屏幕分辨率下做以下的估算就已经足够了：

dx1 = x2 - x1;

dy1 = y2 - y1;

dx2 = x3 - x2;

dy2 = y3 - y2;

dx3 = x4 - x3;

dy3 = y4 - y3; 

len = sqrt(dx1 * dx1 + dy1 * dy1) + 

sqrt(dx2 * dx2 + dy2 * dy2) + 

sqrt(dx3 * dx3 + dy3 * dy3); 

num_steps = int(len * 0.25);

注意，我们在是去锯齿和亚像素精度的前提下来讨论这个的。对于常规的像素精度以及使用 MoveTo/LineTo 接口的情况来说，会有很大的不同。

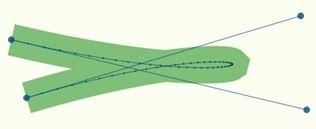
但即使我们这样精确地估算曲线的步进，问题仍然存在。一条三次曲线可能会有非常急的转向，或是很窄的环，甚至是尖端。看下面这个图：

这张图是使用 52 条线段进行近似画出来的曲线。可以看到，使用等距的轮廓(stroke）画出来的环形看起来很不精确。为了使它更准确一些，我们必须要增加中间点的数量。

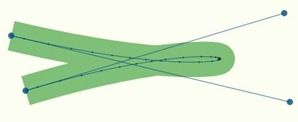
上面我们使用了 210 条线段来画，很明显，大部都是没用的。也就是在曲线“平坦”的部分产生的中间点太多了，而在曲线转弯处的中间点又太少。

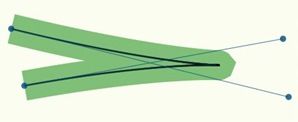
但在使用很小的步进，也还会存在问题：

这条曲线使用了1091条线段，但在转弯处的效果仍然不行。

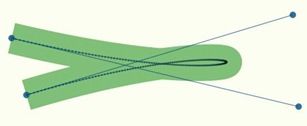
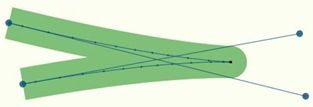
理想状态下，我们需要有一个自适应的步进，能使最终效果看起来如下图所示：

这图中只使用了 40 条线段，但却几乎完美地画出了曲线（考虑到轮廓的效果很好）。这才是我们想要的结果，而且我们的确做到了。你注意看，就算是那个很急的转弯处 stroke 的表现仍然很平滑，而且线段的数量也很合适，在这个例子中，只有 44 条（译注：怎么从 40 到 44 的我也没搞清楚，呵呵）。

Paul de Casteljau Divides and Conquers

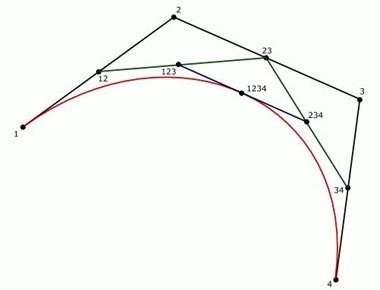
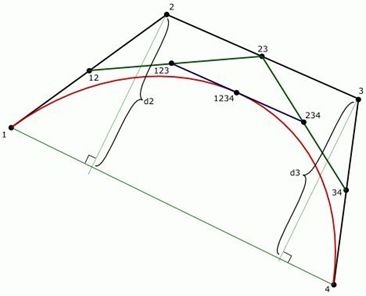
Paul de Casteljau， 雪铁龙（Citroen）的一个非常有才华的工程师，他发现了贝塞尔曲线的一种非常有意思的属性，即，任意角度的曲线都可以被分成两条相同角度的相同曲线（译注：原文是，It's namely that any curve of any degree can be easily divided into two curves of the same degree.我拿不准这里的 degree 是指什么）。下面的图很经典：

我们有 1,2,3,4 四个控制点。计算出它们的中间 12, 23, 34 ，以及“高一阶”的中点 123, 234 ，最后一阶的中间 1234 就落在曲线上了。这里也可以不用中点(系数 t ＝ 0.5)，而使用其它的 0 到 1 之间的系数。但在这篇文章中，我们使用中点。产生的两条新曲线与原曲线完全一致，但新曲线的控制点变成了：1,12,123,1234（左半边），和 1234,234,34,4（右半边）。

很明显，“新”的曲线比原来的曲线要平坦一点，所以，如果我们重复这个过程若干次，我们就可以把用线段来代替曲线。

细分的递归程序代码也相当的经典：

void recursive_bezier(double x1, double y1, 

                      double x2, double y2, 

                      double x3, double y3, 

                      double x4, double y4)

{

    // Calculate all the mid-points of the line segments

    //----------------------

    double x12   = (x1 + x2) / 2;

    double y12   = (y1 + y2) / 2;

    double x23   = (x2 + x3) / 2;

    double y23   = (y2 + y3) / 2;

    double x34   = (x3 + x4) / 2;

    double y34   = (y3 + y4) / 2;

    double x123  = (x12 + x23) / 2;

    double y123  = (y12 + y23) / 2;

    double x234  = (x23 + x34) / 2;

    double y234  = (y23 + y34) / 2;

    double x1234 = (x123 + x234) / 2;

    double y1234 = (y123 + y234) / 2; 

    if(curve_is_flat)

    {

        // Draw and stop

        //----------------------

        draw_line(x1, y1, x4, y4);

    }

    else

    {

        // Continue subdivision

        //----------------------

        recursive_bezier(x1, y1, x12, y12, x123, y123, x1234, y1234); 

        recursive_bezier(x1234, y1234, x234, y234, x34, y34, x4, y4); 

    }

}

就这些！这就是你画一条贝塞尔曲线所需要的一切。不过，魔鬼就在“当曲线是平坦”（代码中的curve_is_flat）的这个条件上。

Estimation of the Distance Error

Casteljau 的细分法有很多优点。我们可以估计曲线的平坦程度，因为我们能得到这方面的信息：即起始点与其它的中间点。而在递增方法中，我们只有一个点的信息。当然，我们可以在计算之前取到最少两个点，然后再分析点的信息，但这样会变得相当的复杂。

停止细分程度有很多种策略，最简单的方法是，直接计算点1和点4之间的距离。这种方法不好，因为点1和点4一开始就可能是重合的，当然，有补救的办法，那就是第一次细分的时候我们强制进行进行。

更好的办法是计算一个点到一条直线的距离，它与估算的误差是成比例的。但问题是，我们应该计算哪段距离？

一开始我觉得计算点1234 到 直接（1-4）的距离就可以了，但，在曲线是“Z”型的时候，比如(100, 100, 200, 100, 100, 200, 200, 200)，这个值为零。

但这种情况可以通过强制进行第一次细分操作来解决。

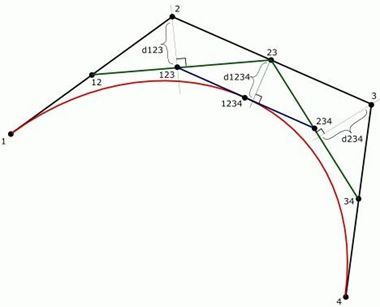
通过进行多次的实验，我发现计算 3 个长度的和会更好：

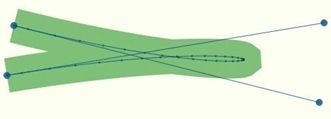
看上图，我们计算了这三个长度的和： d123+d1234+d234 。这个方法不需要特别处理第一次细分的情况。

然后，在进行了更多次的实验之后，我发现计算另两段长度的和会甚至更好，而且这种方法也不需要对第一次细分进行特殊处理。这个和是 d2+d3 ：

就是它了，我们已经得到一个相当好的误差的估算了。计算一个点到一条直线的距离看起来开销不小，但实际上不是这样的，我们不需要计算平方根，要知道，我们要做的只是进行估计，然后对比误差（是或不是）。

所以，代码可以像下面这样写：

void recursive_bezier(double x1, double y1, 

                      double x2, double y2, 

                      double x3, double y3, 

                      double x4, double y4)

{ 

    // Calculate all the mid-points of the line segments

    //----------------------

    double x12   = (x1 + x2) / 2;

    double y12   = (y1 + y2) / 2;

    double x23   = (x2 + x3) / 2;

    double y23   = (y2 + y3) / 2;

    double x34   = (x3 + x4) / 2;

    double y34   = (y3 + y4) / 2;

    double x123  = (x12 + x23) / 2;

    double y123  = (y12 + y23) / 2;

    double x234  = (x23 + x34) / 2;

    double y234  = (y23 + y34) / 2;

    double x1234 = (x123 + x234) / 2;

    double y1234 = (y123 + y234) / 2; 

    // Try to approximate the full cubic curve by a single straight line

    //------------------

    double dx = x4-x1;

    double dy = y4-y1; 

    double d2 = fabs(((x2 - x4) * dy - (y2 - y4) * dx));

    double d3 = fabs(((x3 - x4) * dy - (y3 - y4) * dx)); 

    if((d2 + d3)*(d2 + d3) < m_distance_tolerance * (dx*dx + dy*dy))

    {

        add_point(x1234, y1234);

        return;

    } 

    // Continue subdivision

    //----------------------

    recursive_bezier(x1, y1, x12, y12, x123, y123, x1234, y1234); 

    recursive_bezier(x1234, y1234, x234, y234, x34, y34, x4, y4); 

} 



void bezier(double x1, double y1, 

            double x2, double y2, 

            double x3, double y3, 

            double x4, double y4)

{

    add_point(x1, y1);

    recursive_bezier(x1, y1, x2, y2, x3, y3, x4, y4);

    add_point(x4, y4);

}

m_distance_tolerance 是能接受的最大距离的平方。对于一般的屏幕分辨率，可以取 ： 0.5*0.5＝0.25 。

现在，我们已经解决了通过最少的点来近似整条曲线的问题，误差的最大值是固定的。记得吧，之前的递增方法会产生过多的点，而且在曲线平坦的部分近似误差过少（因为分出来的点过多），而在曲线弯曲处的误则大太。而细分方法可以最小化需要的点的数目，并使得最大误差保持固定。

但这个方法还有很严重的问题。如果点1和点4重合，那么(d2 + d3)*(d2 + d3) 和 (dx*dx + dy*dy)的值都是0 。在这里，浮点数的“小于”和“小于或等于”的比较会产生不同的结果，这是一个很少见的情况。在这种情况下细分会继续下去，而如果结果条件是“小于或等于”的话，则细分会停止。但这样的代码在3个点或4个点重合时会产生栈益出。看起来可以在条件中使用“小于或等于”然后强制进行第一次细分这样的办法来解决。但仔细的分析会发现这办法不行。因为第一次细分后，子曲线然后可能会产生一个环，并有重合的点。这些问题后面都会解决，不过我们先看看如果用角度来估计的话，会是什么样的。

Estimation of Tangent Error

上面的代码，在近似曲线时，用最优的点数保持了固定的最大误差。但它与递增方法一样，在曲线的弯曲处有同样的问题：

这个近似中用了36段线段，最大的误差是0.08个像素。

很显示，仅仅使用长度来估计是不够的。为了让宽画笔（wide strokes）在任何角度都看起来平滑，我们应该对曲率进行估计，而不考虑实际的长度。

细分后，新产生的两条曲线会比原来的曲线平坦。同时点1和点4的角度也一样。如果它们很不一样，曲线在这个点有一个很急的弯曲，那么就要继续进行细分。

注意：

计算角度时我直接使用了 atan2 函数，这个函数开销很大，会明显地降低整个算法的速度。但是值得注意的是它并不总是很重要的。它只在我们需要描画一条等距的曲线时才比较重要，也就是使用非常宽的画笔（stroke）时。如果不是画stroke，或是stroke的宽度小于等于一个像素，那么使用距离来估算就已经可以够好了。

好了，我们现在引入另一个判定标准，m_angle_tolerance :

// If the curvature doesn't exceed the distance_tolerance value

// we tend to finish subdivisions.

//----------------------

if(m_angle_tolerance < curve_angle_tolerance_epsilon)

{

    m_points.add(point_type(x1234, y1234));

    return;

} 



// Angle & Cusp Condition

//----------------------

double a23 = atan2(y3 - y2, x3 - x2);

double da1 = fabs(a23 - atan2(y2 - y1, x2 - x1));

double da2 = fabs(atan2(y4 - y3, x4 - x3) - a23);

if(da1 >= pi) da1 = 2*pi - da1;

if(da2 >= pi) da2 = 2*pi - da2; 

if(da1 + da2 < m_angle_tolerance)

{

    // Finally we can stop the recursion

    //----------------------

    m_points.add(point_type(x1234, y1234));

    return;

}

我们用 m_angle_tolerance 作为标志位，如果这个值小于一个特定值（epsion），那么我们就不再处理角度了。

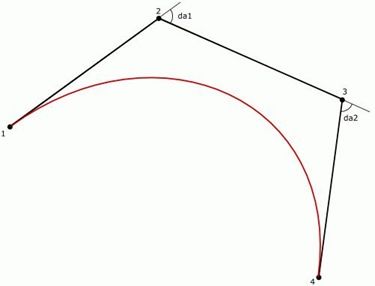
下面的图展示了计算的方法：

嗯，在技术上计算一个角度就够了，比如第一条和第三条线段的夹角（(1-2 and 3-4)，但把两个角都计算出来会另有用处，比如后面提到的尖端的处理方法。

这段代码会认为，两条连续的线段对于计算看起来平滑的 stroke 已经足够了。但它也有问题，首先就是在处理尖端（Cusp）的时候。

Processing of the Cusps

一个三次的（贝塞尔）曲线可以产生一个尖端（cusp），尖端是曲线上切线不连续的点。这种点会使曲线产生一个锐利的转弯，这种转弯无论你怎么放大曲线，看起来都一样的急（Sharp turn）。换句话说，在这个点附近，mitter-join stroke 不可能看起来平滑，因为切线不连续（译注：导数不连续），所以stoke也会产生非常锐利的转弯。

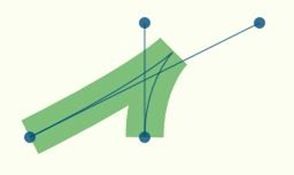
为了产生这样的 cusp ，贝塞点曲线的控制点应该是一个 X 字母的样子：

(100, 100, 300, 200, 200, 200, 200, 100)

在这种情况下，理论上 da1 + da2 < m_angle_tolerance 是不可能产生的，实践中，只要4个点重合在一起，那么条件就成立了，所有atan2调用的参数都会是 0 。这时，递归层次会非常非常深，很可能会产生一个栈益出。那很不好，不过好在有一个很简单的解决办法：

if(da1 > m_cusp_limit)

{

    m_points.add(point_type(x2, y2));

    return;

}



if(da2 > m_cusp_limit)

{

    m_points.add(point_type(x3, y3));

    return;

}

 

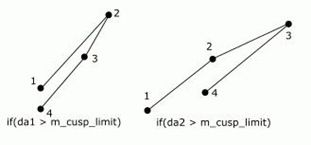
注意，我们通常会使用的是曲线上的点1234 ，因为它使得我们可以对称地处理端点。但在这里，我们用的点是尖端点，我是经过多次实验后产生这个想法的，这就保证了 stroke 的截面是垂直于尖端点的。

附记：

一开始我实验时只考虑角度这一个条件，这让曲线在转弯时始终保持平滑，而且轮廓看起来也很漂亮，但在平坦的部分看起来不够准确。最后我得到这样的结论：只有结合着距离和角度两个条件，才能使用尽量少的点数产生平滑的stroke 。

The Devil is in the Details

但那还不够好！有很多病态的例子可以使得这个算法失败。我花了很长的时候去分析这些情况，并希望通过加些一些什么东西以一劳永逸地解决所有问题。如果考虑到所有情况的话，那么整个代码会成变成一陀乱麻，我讨厌这样的代码。比如说，有点重合的时候会导致角度计算失败，或是，在某种情况下，atan2(0,0)会返回0,比如水平直线。现在，我跳过所有我遇到的痛苦，给你一个我的结论：

我的实验显示，所有病态情况都可以对付“同在一条直线”( collinear case )的方法来应对。

为了估计距离，我们有下面的计算式：

double dx = x4-x1;

double dy = y4-y1;

double d2 = fabs(((x2 - x4) * dy - (y2 - y4) * dx));

double d3 = fabs(((x3 - x4) * dy - (y3 - y4) * dx));

如果用 d2 除以 line1-4，我们就可以得到点2到直接1-4的距离，不过，就像早先提到的一样，我们并不需要真实的距离长度，只是用来进行比较就可以了。在实践中也就意味着如果我们引入一个  curve_collinearity_epsilon ，我们可以过滤掉重合的点，和其它各点同线的情况。

double dx = x4-x1;

double dy = y4-y1; 

double d2 = fabs(((x2 - x4) * dy - (y2 - y4) * dx));

double d3 = fabs(((x3 - x4) * dy - (y3 - y4) * dx)); 



if(d2 > curve_collinearity_epsilon && d3 > curve_collinearity_epsilon)

{ 

    // Regular care

    . . .

}

else

{

    if(d2 > curve_collinearity_epsilon)

    {

        // p1,p3,p4 are collinear (or coincide), p2 is considerable

        . . .

    }

    else

        if(d3 > curve_collinearity_epsilon)

        {

            // p1,p2,p4 are collinear (or coincide), p3 is considerable

            . . .

        }

        else

        {

            // Collinear case

           . . .

        }

}

在各点同线的情况下（或是有重合点的情况下）我们要用不同的方法。其中有一种情况是四个点都在一条直线上。惊奇的是，是否同线的检查可以让我们在曲线有尖端的情况下远离深度的递归。我们可以不对尖端进行限制，对掉相关的代码。但我仍然保留了这些代码，因为在某些情况下，这些代码会有用。