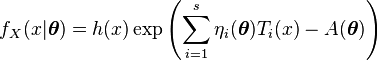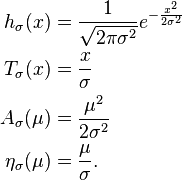[MCSM]Exponential family: 指数分布族
Exponential family(指数分布族)是一个经常出现的概念,但是对其定义并不是特别的清晰,今天好好看了看WIKI上的内容,有了一个大致的了解,先和大家分享下。本文基本是WIKI上部分内容的翻译。
1. 几个问题
什么是指数分布族?
既然是”族“,那么族内的共同特点是什么?
为何指数分布族被广泛应用?是指数分布族选择了我们,还是我们选择了指数分布族?(这个问题没有回答,需要结合具体实例分析)
2. 参考
Exponential family. (2015, February 26). In Wikipedia, The Free Encyclopedia. Retrieved 05:00, April 3, 2015, from http://en.wikipedia.org/w/index.php?title=Exponential_family&oldid=648989632
3. 指数分布族: 定义
指数分布族指概率分布满足以下形式的分布
其中($\theta$,$x$也可以是标量)
Exponential family ,也称 Exponential Class,包括了很多常见的分布。譬如
normal, exponential, gamma, chi-squared, beta, Dirichlet, Bernoulli, categorical, Poisson, Wishart, Inverse Wishart.
分布函数中的T (x ) , η (θ ) 和 A(η )并不是任意定义的,每一部分都有其特殊的意义。
T (x )是分布的充分统计量(sufficient statistic )
η 是自然参数。对于有限的函数![]() 而言, η 的集合被称为自然参数空间。
而言, η 的集合被称为自然参数空间。
A(η )被称为对数配分函数(partition function ),实际上它是归一化因子的对数形式。它使得概率分布积分为1的条件得到满足。
上式可以看出,通过对 A(η )求导,容易得到充分统计量T (x )的均值,方差和其他性质。(怎么求?)
4. 指数分布族:性质
指数分布族具有很多性质,这些性质使得指数分布族在统计分析具有重要作用。并且在很多情况下,只有指数分布族具有那些性质。其中包括
不太懂,怕弄错,还是给原文好了。
|
具体解释如下(没看到的就不解释了……):
(1) 指数函数的充分统计量的可以从大量的i.i.d.数据中归结为估计的几个值(即T (x )),这点在 sufficient statistics中也有说明
| According to the Pitman–Koopman–Darmois theorem, among families of probability distributions whose domain does not vary with the parameter being estimated, only in exponential families is there a sufficient statistic whose dimension remains bounded as sample size increases. Less tersely, suppose This theorem shows that sufficiency (or rather, the existence of a scalar or vector-valued of bounded dimension sufficient statistic) sharply restricts the possible forms of the distribution. |
(2)指数分布族具有共轭先验特性。可参考本文“术语解释”。
5. 指数分布族:举例
正态分布
这是单参数的指数分布族,可以被写为如下标准形式。
更多可参考WIKIPEDIA。
6. 术语解释
independent identically distributed独立同分布(i.i.d.)
如果在一组随机变量集合中,任意一随机变量都有相同的概率分布,并且相互之间独立,那么则称变量集独立同分布。
sufficient statistic充分统计量
统计量T(X ) 对于给定参数θ 而言是充分的 是指对于X 的条件概率而言, 给定统计量T (X ), 则不依赖于参数 θ。
一种更容易理解的方式是(参考Steven M.Kay《统计信号处理基础》),充分统计量是不止一个的。对于要估计的参数θ 来说,观测到数据集合显然是充分统计量。而充分代表着一旦给定了充分统计量,那么参数的条件概率和其他统计量无关。
上述两个式子是等价的。通过贝叶斯公式可以互相推导得到。
太长了,没看。是归一化参数的一种特殊情况,这里简单的理解为归一化参数就好。
conjugate priors 共轭先验(不知道是否应该这样翻译)
在贝叶斯概率理论中,如果后验概率分布p(θ|x )和先验概率分布p(θ)同属于一种概率分布族,那么后验和先验称为共轭分布。同时这一先验被称为在此似然函数下的共轭先验。
贝叶斯定理有
给定似然函数(通过观察结果,这通常来说是很好的到的),上式的积分求解的难度和先验知识有关。在某些选择下,后验概率分布和先验概率分布具有类似的代数结构。
共轭先验性质给出了后验概率分布的闭式节,否则我们需要求解复杂的积分。而且,共轭先验使得我们能够清楚的看到似然函数对概率分布的影响。