Tail Recursion, Recursion, Concepts and Examples
http://c2.com/cgi/wiki?TailRecursion
Recursive procedures call themselves to work towards a solution to a problem.
In simple implementations this balloons the stack as the nesting gets deeper and deeper,
reaches the solution, then returns through all of the stack frames.
This waste is a common complaint about recursive programming in general.
A function call is said to be tail recursive if there is nothing to do after the function returns except return its value.
Since the current recursive instance is done executing at that point, saving its stack frame is a waste.
Specifically, creating a new stack frame on top of the current, finished, frame is a waste.
A compiler is said to implement TailRecursion if it recognizes this case and replaces the caller in place with the callee,
so that instead of nesting the stack deeper, the current stack frame is reused.
This is equivalent in effect to a "GoTo", and lets a programmer write recursive definitions
without worrying about space inefficiency (from this cause) during execution.
TailRecursion is then as efficient as iteration normally is.
Consider this recursive definition of the factorial function in C:
int factorial( n ) { if ( n == 0 ) return 1; return n * factorial( n - 1 ); }
This definition is not tail-recursive since the recursive call to factorial is not the last thing in the function
(its result has to be multiplied by n). But watch this:
int factorial1( n, accumulator ) { if ( n == 0 ) return accumulator; return factorial1( n - 1, n * accumulator ); } int factorial( n ) { return factorial1( n, 1 ); }
The tail-recursion of factorial1 can be equivalently defined in terms of goto:
int factorial1( n, accumulator ) { beginning: if ( n == 0 ) return accumulator; else { accumulator *= n; n -= 1; goto beginning; } }
From the goto version, we can derive a version that uses C's built-in control structures:
int factorial1( n, accumulator ) { while ( n != 0 ) { accumulator *= n; n -= 1; } return accumulator; }
The simple C example illustrates a case where the recursive call could be optimized into a goto.
As far as we know, neither common Perl nor C implementations do this. Does anyone know better?
http://phoenix.goucher.edu/~kelliher/cs23/feb21.html
Recursion, Concepts and Examples
Tom Kelliher, CS23
Feb. 21, 1996
The Stack Model of Program Execution
How does a program use memory?
- Code --- code segment
- Static items --- data segment
- Local items --- stack (segment)
- Dynamic items --- heap
What's a stack?
Terminology:
- Push
- Pop
- Activation record
Contents of activation record:
- Return address
- Initialized actual arguments
- Uninitialized locals
- Return value
- Stack bookkeeping info.
Created by calling function, used by called function
Idea:
- Each time function called, activation pushed
- Function executes (possibly causing further pushes)
- Each time function returns, activation popped
Recursion
- What is it?
- Divide and conquer
- base case
What do I need?
- Decomposition into smaller problems of same type
- Recursive calls must diminish problem size
- Necessity of base case
- Base case must be reached
Box Trace Example
Consider the code fragment:
main( ) { int i = 4; // 1 cout << f( i ) << endl; // 2 i++; // 3 cout << f( i ) << endl; // 4 } int f( int a1 ) { if ( a1 <= 1 ) // 5 return 1; // 6 else // 7 return a1 * f( a1 - 1 ); // 8 }
Box trace yourselves:
#include <iostream.h> int BinSearch( const int A[ ], int First, int Last, int Value ) // --------------------------------------------------------- // Searches the array elements A[First] through A[Last] // for Value by using a binary search. // Precondition: 0 <= First, Last <= SIZE - 1, where // SIZE is the maximum size of the array, and // A[First] <= A[First+1] <= ... <= A[Last]. // Postcondition: If Value is in the array, returns // the index of the array element that equals Value; // otherwise returns -1. // --------------------------------------------------------- { if ( First > Last ) return -1; // Value not in original array else { // Invariant: If Value is in A, // A[First] <= Value <= A[Last] int Mid = ( First + Last ) / 2; if ( Value == A[ Mid ] ) return Mid; // Value found at A[Mid] else if ( Value < A[ Mid ] ) return BinSearch( A, First, Mid - 1, Value ); // X else return BinSearch( A, Mid + 1, Last, Value ); // Y } // end else } // end BinSearch
Assume the array holds: 1, 5, 9, 12, 15, 21, 29, 31
Search for: 5, 13
Efficiency of Recursion
Costs:
- Function call, return
- Repeated solution of same sub-problems
Consider:
int fib( int val ) { if ( val <= 2 ) return 1; else return fib( val - 1 ) + fib( val - 2 ); }
Call graph for fib(6):
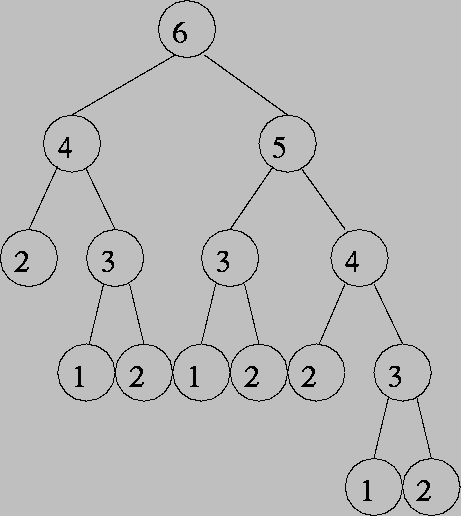
Tail Recursion
A function is tail recursive if the very last thing it does is make its recursive call.
Example:
void printLinkedList( list* l ) { if ( l != NULL ) { cout << l->fname << " " << l->lname << endl; printLinkedList( l->next ); } }
Are fact(), fib() tail recursive?
Head Recursion
What is it?
Write a recursive function which prints a reversed string
Is it head recursive?
Utility of head recursion
Example 1
Write a recursive function which computes pow(n, i).
int pow( int n, int i ) { if ( i == 0 ) return 1; else if ( i == 1 ) return n; else { int partial = pow( n, i / 2 ); if ( i % 2 == 0 ) return partial * partial; else return partial * partial * n; } }
More efficient than iterative solution?
Example 2
How is an array an example of a recursive data structure?
What does the following function do? Assume that it is called this way:
int d[ 3 ] = { 3, 89, 47 }; f(d, 3);
Here's the function:
void f( int d[ ], int n ) { if ( n != 0 ) { cout << d[ n - 1 ] << endl; f( d, n - 1 ); } }
What does this version do?
void f( int d[ ], int n ) { if ( n != 0 ) { cout << d[ 0 ] << endl; f( d + 1, n - 1 ); } }