Timus 1008. Image encoding
Timus 1008. Image encoding 讨论黑白图像的编码问题。
Problem Source: Third Open USTU Collegiate Programming Contest (PhysTech Cup), March 18, 2000
返回目录
1008. Image encoding
Time Limit: 2.0 second
Memory Limit: 16 MB
Memory Limit: 16 MB

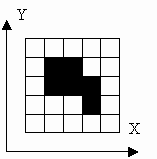
There are several ways to encode an image. In this problem we will consider two representations of an image. We assume that the image consists of black and white pixels. There is at least one black pixel and all black pixels are connected with their sides. Coordinates of black pixels are not less than 1 and not greater than 10. An example of such an image is at the figure.
Both representations describe arrangement of black pixels only.
At the first representation we specify in the first line number of black pixels and coordinates of each black pixel in the following lines. Pixels are listed in order of increasing X. In case of equality of X they are listed in order of increasing Y. Image at the figure is encoded as follows:
6
2 3
2 4
3 3
3 4
4 2
4 3
2 3
2 4
3 3
3 4
4 2
4 3
At the second representation we specify in the first line coordinates of the lowest left black pixel. Each of the following lines contains a description of neighbors for one of the pixels. At first, neighbors of the lowest left pixel are specified, then neighbors of its first neighbor (if it exists) are specified, then neighbors of its second neighbor (if it also exists) follow. When all its neighbors are described the description of the neighbors of its first neighbor follows. The description of the neighbors of its second neighbor follows then and so on.
Each descriptive line contains at most one letter for each neighbor: R for the right, T for the top, L for the left, B for the bottom. If the neighbor was already specified it is not included into the descriptive line and vice-versa. Also there is only one descriptive line for each pixel. Neighbors are listed counter-clockwise starting with the right. Each descriptive line ends with ",". Last line ends with "." instead of ",". Image at the figure is encoded as follows:
2 3
RT,
RT,
,
B,
,
.
RT,
RT,
,
B,
,
.
There are no leading or tailing spaces in any representation. There is exactly one space between X and Y coordinates.
Input
One representation of the image will be given to your program in the input.
Output
Your program has to write other representation of the image to the output.
Sample
| input | output |
|---|---|
| 6 2 3 2 4 3 3 3 4 4 2 4 3 |
2 3 RT, RT, , B, , . |
解答如下:
1
using
System;
2 using System.IO;
3 using System.Drawing;
4 using System.Collections.Generic;
5
6 namespace Skyiv.Ben.Timus
7 {
8 // http://acm.timus.ru/problem.aspx?space=1 &num=1008
9 sealed class T1008
10 {
11 static readonly Size[] direction = { new Size( 1 , 0 ), new Size( 0 , 1 ), new Size( - 1 , 0 ), new Size( 0 , - 1 ) };
12 static readonly string letter = " RTLB " ; // Right, Top, Left, Bottom
13 bool [,] image = new bool [ 12 , 12 ];
14
15 static void Main()
16 {
17 new T1008().Run(Console.In, Console.Out);
18 }
19
20 void Run(TextReader reader, TextWriter writer)
21 {
22 string [] ss = reader.ReadLine().Split();
23 if (ss.Length < 2 ) Write2(writer, Read1(reader, int .Parse(ss[ 0 ])));
24 else Write1(writer, Read2(reader, new Point( int .Parse(ss[ 0 ]), int .Parse(ss[ 1 ]))));
25 }
26
27 Point Read1(TextReader reader, int lines)
28 {
29 Point first = Point.Empty;
30 for ( int i = 0 ; i < lines; i ++ )
31 {
32 string [] ss = reader.ReadLine().Split();
33 Point p = new Point( int .Parse(ss[ 0 ]), int .Parse(ss[ 1 ]));
34 image[p.X, p.Y] = true ;
35 if (i == 0 ) first = p;
36 }
37 return first;
38 }
39
40 void Write1(TextWriter writer, int cnt)
41 {
42 writer.WriteLine(cnt);
43 for ( int i = 0 ; i < image.GetLength( 0 ); i ++ )
44 for ( int j = 0 ; j < image.GetLength( 1 ); j ++ )
45 if (image[i, j]) writer.WriteLine(i + " " + j);
46 }
47
48 int Read2(TextReader reader, Point first)
49 {
50 int cnt = 1 ;
51 image[first.X, first.Y] = true ;
52 Queue < Point > queue = new Queue < Point > ();
53 queue.Enqueue(first);
54 while (queue.Count > 0 )
55 {
56 Point p, q = queue.Dequeue();
57 string s = reader.ReadLine();
58 for ( int idx, i = 0 ; ; i ++ , cnt ++ )
59 {
60 if ((idx = letter.IndexOf(s[i])) < 0 ) break ;
61 queue.Enqueue(p = q + direction[idx]);
62 image[p.X, p.Y] = true ;
63 }
64 }
65 return cnt;
66 }
67
68 void Write2(TextWriter writer, Point first)
69 {
70 writer.WriteLine(first.X + " " + first.Y);
71 image[first.X, first.Y] = false ;
72 Queue < Point > queue = new Queue < Point > ();
73 queue.Enqueue(first);
74 while (queue.Count > 0 )
75 {
76 Point q = queue.Dequeue();
77 for ( int i = 0 ; i < direction.Length; i ++ )
78 {
79 Point p = q + direction[i];
80 if ( ! image[p.X, p.Y]) continue ;
81 queue.Enqueue(p);
82 image[p.X, p.Y] = false ;
83 writer.Write(letter[i]);
84 }
85 writer.WriteLine((queue.Count > 0 ) ? " , " : " . " );
86 }
87 }
88 }
89 }
2 using System.IO;
3 using System.Drawing;
4 using System.Collections.Generic;
5
6 namespace Skyiv.Ben.Timus
7 {
8 // http://acm.timus.ru/problem.aspx?space=1 &num=1008
9 sealed class T1008
10 {
11 static readonly Size[] direction = { new Size( 1 , 0 ), new Size( 0 , 1 ), new Size( - 1 , 0 ), new Size( 0 , - 1 ) };
12 static readonly string letter = " RTLB " ; // Right, Top, Left, Bottom
13 bool [,] image = new bool [ 12 , 12 ];
14
15 static void Main()
16 {
17 new T1008().Run(Console.In, Console.Out);
18 }
19
20 void Run(TextReader reader, TextWriter writer)
21 {
22 string [] ss = reader.ReadLine().Split();
23 if (ss.Length < 2 ) Write2(writer, Read1(reader, int .Parse(ss[ 0 ])));
24 else Write1(writer, Read2(reader, new Point( int .Parse(ss[ 0 ]), int .Parse(ss[ 1 ]))));
25 }
26
27 Point Read1(TextReader reader, int lines)
28 {
29 Point first = Point.Empty;
30 for ( int i = 0 ; i < lines; i ++ )
31 {
32 string [] ss = reader.ReadLine().Split();
33 Point p = new Point( int .Parse(ss[ 0 ]), int .Parse(ss[ 1 ]));
34 image[p.X, p.Y] = true ;
35 if (i == 0 ) first = p;
36 }
37 return first;
38 }
39
40 void Write1(TextWriter writer, int cnt)
41 {
42 writer.WriteLine(cnt);
43 for ( int i = 0 ; i < image.GetLength( 0 ); i ++ )
44 for ( int j = 0 ; j < image.GetLength( 1 ); j ++ )
45 if (image[i, j]) writer.WriteLine(i + " " + j);
46 }
47
48 int Read2(TextReader reader, Point first)
49 {
50 int cnt = 1 ;
51 image[first.X, first.Y] = true ;
52 Queue < Point > queue = new Queue < Point > ();
53 queue.Enqueue(first);
54 while (queue.Count > 0 )
55 {
56 Point p, q = queue.Dequeue();
57 string s = reader.ReadLine();
58 for ( int idx, i = 0 ; ; i ++ , cnt ++ )
59 {
60 if ((idx = letter.IndexOf(s[i])) < 0 ) break ;
61 queue.Enqueue(p = q + direction[idx]);
62 image[p.X, p.Y] = true ;
63 }
64 }
65 return cnt;
66 }
67
68 void Write2(TextWriter writer, Point first)
69 {
70 writer.WriteLine(first.X + " " + first.Y);
71 image[first.X, first.Y] = false ;
72 Queue < Point > queue = new Queue < Point > ();
73 queue.Enqueue(first);
74 while (queue.Count > 0 )
75 {
76 Point q = queue.Dequeue();
77 for ( int i = 0 ; i < direction.Length; i ++ )
78 {
79 Point p = q + direction[i];
80 if ( ! image[p.X, p.Y]) continue ;
81 queue.Enqueue(p);
82 image[p.X, p.Y] = false ;
83 writer.Write(letter[i]);
84 }
85 writer.WriteLine((queue.Count > 0 ) ? " , " : " . " );
86 }
87 }
88 }
89 }
这道题目讨论的黑白图像至少包含一个黑色象素,且所有的黑色像素都是连通的。我们考虑两种对黑色象素进行编码的方案。
第一种编码方案在第一行给出黑色象素的数目,在接下来的行中给出黑色象素的坐标,该坐标是排好序的。
第二种编码方案在第一行中给出左下角黑色象素的坐标。接下来的行依次描述每个黑色象素的邻居,每个邻居用一个英文字母表示:R:右、T:顶、L:左、B:底,已经描述过的邻居不再描述,每一行以逗号结束,最后一行以句号结束。
现在给出某幅黑白图像的一种编码,要求你写一个程序输出该图像的另一种编码。
在上述程序中,第 13 行的布尔矩阵 image 用来在内存中表示该黑白图像。
第 20 到 25 行的 Run 方法根据输入的第一行判断该黑白图像是采用哪种方案编码的,然后调用相应的方法进行处理。
第 27 到 38 行的 Read1 方法读取第一种编码方案的输入到 image 矩阵中,并返回该黑白图像左下角黑色象素的坐标。
第 40 到 46 行的 Write1 方法将 image 矩阵按第一种编码方案输出,其中 cnt 表示黑色象素的数目。
第 48 到 66 行的 Read2 方法读取第二种编码方案的输入到 image 矩阵中,并返回该黑白图像中黑色象素的数目。第 52 行的 queue 队列用来记录黑色象素的坐标。第 54 行开始的循环依次读入各个黑色象素。
第 68 到 87 行的 Write2 方法将 image 矩阵按第二种编码方案输出,其中 first 表示该黑白图像左下角黑色象素的坐标。第 72 行的 queue 队列用来记录黑色象素的坐标。第 74行开始的循环使用广度优先搜索算法来寻找黑色象素。
返回目录