聚类算法之顺序聚类

1.    顺序聚类

事实上，将n个对象，聚类到k个聚类中这件事本身是一个NP难问题。熟悉组合数学应该知道这个问题的解事第二类Stirling数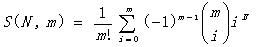：。这样问题也就出现了，如果k值固定，那么计算还是可行的，如果k值不固定，就要对所有的可能k都进行计算，那运行时间可想而知了。然而并不是所有的可行聚类方案都是合理的，所谓的合理，我理解就是说接近你的聚类目标的，之所以我们要分类，必然有初始动机，那么可以根据这个动机制定可行的聚类方案，这样，复杂度的问题就回避了。

顺序算法（sequential algorithms）是一种非常简单的聚类算法，大多数都至少将所有特征向量使用一次或几次，最后的结果依赖于向量参与算法的顺序。这种聚类算法一般是不预先知道聚类数量k的，但有可能给出一个聚类数上界q。本文将主要介绍基本顺序算法（Basic Sequential Algorithmic Scheme,BSAS）和其几个变种，并给出代码实现。

首先看BSAS，这个算法方案需要用户定义参数：不相似性阈值θ和允许的最大聚类数q。算法的基本思想：由于要考虑每个新向量，根据向量到已有聚类的距离，将它分配到一个已有的聚类中，或者一个新生成的聚类中。算法的伪码描述如下：

1.       m=1   /*{聚类数量}*/

2.       C_m={x₁}

3.       For i=2 to N

4.           找C_k: d(x_i,C_k)=min_1£j£md(x_i,C_j)

5.           If (d(x_i,C_k)>Θ) AND (m<q) then

6.               m=m+1

7.               C_m={x_i}

8.           Else

9.               C_k=C_kÈ{x_i}

10.           如果需要，更新向量表达

11.       End {if}

12.   End {for}

由上面的描述可以看出BSAS算法对向量顺序非常依赖，无论是聚类数量还是聚类本身，不同的向量顺序会导致完全不同的聚类结果。另一个影响聚类算法结果的重要因素是阈值θ的选择，这个值直接影响最终聚类的数量，如果θ太小，就会生成很多不必要的聚类，因为很多情况下向量与聚类的合并条件都受到θ的限制，而如果θ太大，则聚类数量又会不够。BSAS比较适合致密聚类，其对数据集进行一次扫描，每次迭代中计算当前向量与聚类间的距离，因为最后的聚类数m被认为远小于N，故BSAS的时间复杂度为O(N)。

由于BSAS算法依赖于q，因此这里介绍一种自动估计聚类数q的简单方法，该方法也适用于其他的聚类算法，令BSAS(Θ)为具有给定不相似阈值θ的BSAS算法。

1.       For Θ=a to b step c

2.          算法BSAS(Θ)执行s次，每一次都使用不同的顺序表示数据。

3.          估计聚类数，m_Θ作为从s次BSAS(Θ)算法得来的最常出现的聚类数。

4.       Next Θ

其中a和b是数据集的所有向量对的最小和最大不相似级别，c的选择直接受d(x,C)的影响。

2. 算法实现

package  util.clustering;

import  java.util.ArrayList;
import  java.util.Collection;
import  java.util.Iterator;
import  java.util.List;

/**
 * @author Jia Yu
 *
 */
public   class  BSAS  < T  extends  Clusterable < T >>   {

    /**
     * Basic Sequential Algorithmic Scheme
     * 适用于致密聚类
     */
    
    public BSAS() {
    }
    
    /**
     * Basic Sequential Algorithmic Scheme
     * 考虑样本空间中每个向量，根据向量到已有的聚类中心的距离，将它分配到一个已有聚类中，或者一个新生成的聚类中。
     * time complexity is O(N)
     * BSAS算法对整个数据集只进行一次扫描。
     * @param points 待聚类的向量
     * @param Phi 用户定义的不相似性阈值
     * @param q 用户定义的允许的最大聚类数
     * @return
     */
    public List<Cluster<T>> cluster(final Collection<T> points,final double Phi,final int q){
        int m = 0;
        int n = points.size();
        double disOfXandCj = 0;
        double disOfXandCk;
        List<T> ptList = new ArrayList<T>(points);
        Cluster<T> C = new Cluster<T>(ptList.get(m));
        C.addPoint(ptList.get(m));
        Cluster<T> Ck = C;
        List<Cluster<T> > cList = new ArrayList<Cluster<T> >();
        cList.add(C);
        for(int i=1;i<n;i++){
            disOfXandCk = Double.MAX_VALUE;
            Iterator<Cluster<T> > cListIt = cList.iterator(); 
            while(cListIt.hasNext()){
                Cluster<T> Cj = cListIt.next();
                disOfXandCj = getDisOfPointAndCluster(ptList.get(i),Cj);
                if(disOfXandCk > disOfXandCj){
                    disOfXandCk = disOfXandCj;
                    Ck = Cj;
                }
            }
            if(disOfXandCk > Phi && m < q){            //不满足条件，则产生新的聚类
                m++;
                Cluster<T> cm = new Cluster<T>(ptList.get(i));
                cm.addPoint(ptList.get(i));
                cList.add(cm);
            }
            else{            //满足条件的将点加入已有聚类，并更新聚类中心
                if(cList.contains(Ck))
                    cList.remove(Ck);
                Ck.addPoint(ptList.get(i));
                final T newCenter = Ck.getCenter().centroidOf(Ck.getPoints());
                Cluster<T> tempCluster = new Cluster<T>(newCenter);
                for(int j=0;j<Ck.getPoints().size();j++){
                    tempCluster.addPoint(Ck.getPoints().get(j));
                }
                cList.add(tempCluster);
            }
        }
        return cList;
    }

    /**
     * 选择不同的测度，有不同的算法。
     * 这里默认dis(x,C)为点到聚类中心的距离。
     */
    private double getDisOfPointAndCluster(T t, Cluster<T> cj) {
        return t.distanceFrom(cj.getCenter());
    }

}

3. 程序框架

       我的聚类程序主要扩展自Apache Commons Math开源框架，下面是其结构，我简单加入了Clusterer类作为抽象模板类，使用模板方法模式修改了框架，为后续加入的例如BSAS算法提供模板。

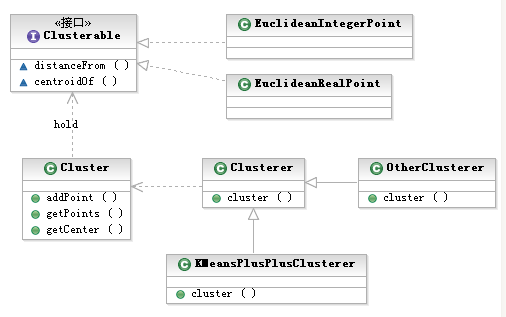
4. 小结

       顺序算法简单易实现，对于学习聚类来说是入门的最好选择，考虑到篇幅的限制，不能将代码全部发上来，如果有需要可以向我索要，Apache Commons Math框架可以到Apache的网站上下载。另外还有很多介绍不够详细，感兴趣的朋友可以继续深入研究BSAS的扩展。

5. 参考文献及推荐阅读

[1]Pattern Recognition Third Edition, Sergios Theodoridis, Konstantinos Koutroumbas

[2]模式识别第三版, Sergios Theodoridis, Konstantinos Koutroumbas著, 李晶皎, 王爱侠, 张广源等译