基于Python实现粒子滤波效果

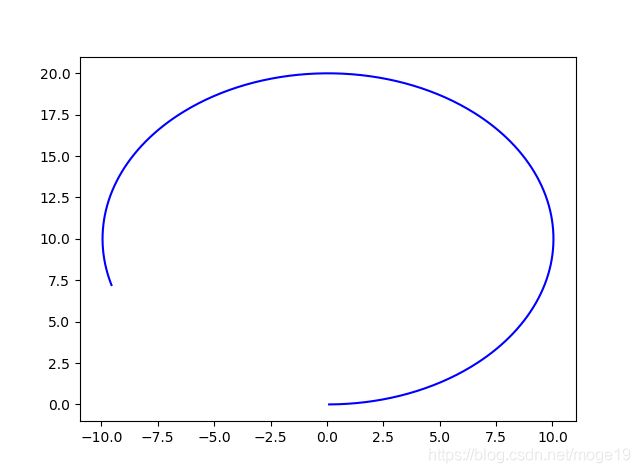
1、建立仿真模型

（1）假设有一辆小车在一平面运动，起始坐标为[0，0]，运动速度为1m/s，加速度为0.1 m / s 2 m/s^2 m/s2，则可以建立如下的状态方程：
Y = A ∗ X + B ∗ U Y=A*X+B*U Y=A∗X+B∗U
U为速度和加速度的的矩阵
U = [ 1 0.1 ] U= \begin{bmatrix} 1 \\ 0.1\\ \end{bmatrix} U=[10.1​]
X为当前时刻的坐标，速度，加速度
X = [ x y y a w V ] X= \begin{bmatrix} x \\ y \\ yaw \\ V \end{bmatrix} X=⎣⎢⎢⎡​xyyawV​⎦⎥⎥⎤​
Y为下一时刻的状态
则观察矩阵A为：
A = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 ] A= \begin{bmatrix} 1&0 & 0 &0 \\ 0 & 1 & 0&0 \\ 0 & 0 &1 &0 \\ 0&0 & 0 &0 \end{bmatrix} A=⎣⎢⎢⎡​1000​0100​0010​0000​⎦⎥⎥⎤​
矩阵B则决定小车的运动规矩，这里取B为：
B = [ c o s ( x ) ∗ t 0 s i n ( x ) ∗ t 0 0 t 1 0 ] B= \begin{bmatrix} cos(x)*t &0\\ sin(x)*t &0\\ 0&t\\ 1&0 \end{bmatrix} B=⎣⎢⎢⎡​cos(x)∗tsin(x)∗t01​00t0​⎦⎥⎥⎤​
python编程实现小车的运动轨迹:

"""

Particle Filter localization sample

author: Atsushi Sakai (@Atsushi_twi)

"""

import math

import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.transform import Rotation as Rot


DT = 0.1 # time tick [s]
SIM_TIME = 50.0 # simulation time [s]
MAX_RANGE = 20.0 # maximum observation range

# Particle filter parameter
NP = 100 # Number of Particle
NTh = NP / 2.0 # Number of particle for re-sampling

def calc_input():
  v = 1.0 # [m/s]
  yaw_rate = 0.1 # [rad/s]
  u = np.array([[v, yaw_rate]]).T
  return u

def motion_model(x, u):
  F = np.array([[1.0, 0, 0, 0],
         [0, 1.0, 0, 0],
         [0, 0, 1.0, 0],
         [0, 0, 0, 0]])

  B = np.array([[DT * math.cos(x[2, 0]), 0],
         [DT * math.sin(x[2, 0]), 0],
         [0.0, DT],
         [1.0, 0.0]])

  x = F.dot(x) + B.dot(u)

  return x

def main():
  print(__file__ + " start!!")

  time = 0.0
  # State Vector [x y yaw v]'
  x_true = np.zeros((4, 1))
  
  x = []
  y = []

  while SIM_TIME >= time:
    time += DT
    u = calc_input()

    x_true = motion_model(x_true, u)
    
    x.append(x_true[0])
    y.append(x_true[1])
    
  plt.plot(x,y, "-b")
    
if __name__ == '__main__':
  main()

运行结果：

2、生成观测数据

实际运用中，我们需要对小车的位置进行定位，假设坐标系上有4个观测点，在小车运动过程中，需要定时将小车距离这4个观测点的位置距离记录下来，这样，当小车下一次寻迹时就有了参考点；

def observation(x_true, xd, u, rf_id):
  x_true = motion_model(x_true, u)

  # add noise to gps x-y
  z = np.zeros((0, 3))

  for i in range(len(rf_id[:, 0])):

    dx = x_true[0, 0] - rf_id[i, 0]
    dy = x_true[1, 0] - rf_id[i, 1]
    d = math.hypot(dx, dy)
    if d <= MAX_RANGE:
      dn = d + np.random.randn() * Q_sim[0, 0] ** 0.5 # add noise
      zi = np.array([[dn, rf_id[i, 0], rf_id[i, 1]]])
      z = np.vstack((z, zi))

  # add noise to input
  ud1 = u[0, 0] + np.random.randn() * R_sim[0, 0] ** 0.5
  ud2 = u[1, 0] + np.random.randn() * R_sim[1, 1] ** 0.5
  ud = np.array([[ud1, ud2]]).T

  xd = motion_model(xd, ud)

  return x_true, z, xd, ud

3、实现粒子滤波

#
def gauss_likelihood(x, sigma):
  p = 1.0 / math.sqrt(2.0 * math.pi * sigma ** 2) * \
    math.exp(-x ** 2 / (2 * sigma ** 2))

  return p

def pf_localization(px, pw, z, u):
  """
  Localization with Particle filter
  """

  for ip in range(NP):
    x = np.array([px[:, ip]]).T
    w = pw[0, ip]

    # 预测输入
    ud1 = u[0, 0] + np.random.randn() * R[0, 0] ** 0.5
    ud2 = u[1, 0] + np.random.randn() * R[1, 1] ** 0.5
    ud = np.array([[ud1, ud2]]).T
    x = motion_model(x, ud)

    # 计算权重
    for i in range(len(z[:, 0])):
      dx = x[0, 0] - z[i, 1]
      dy = x[1, 0] - z[i, 2]
      pre_z = math.hypot(dx, dy)
      dz = pre_z - z[i, 0]
      w = w * gauss_likelihood(dz, math.sqrt(Q[0, 0]))

    px[:, ip] = x[:, 0]
    pw[0, ip] = w

  pw = pw / pw.sum() # 归一化

  x_est = px.dot(pw.T)
  p_est = calc_covariance(x_est, px, pw)
  #计算有效粒子数
  N_eff = 1.0 / (pw.dot(pw.T))[0, 0] 
  #重采样
  if N_eff < NTh:
    px, pw = re_sampling(px, pw)
  return x_est, p_est, px, pw


def re_sampling(px, pw):
  """
  low variance re-sampling
  """

  w_cum = np.cumsum(pw)
  base = np.arange(0.0, 1.0, 1 / NP)
  re_sample_id = base + np.random.uniform(0, 1 / NP)
  indexes = []
  ind = 0
  for ip in range(NP):
    while re_sample_id[ip] > w_cum[ind]:
      ind += 1
    indexes.append(ind)

  px = px[:, indexes]
  pw = np.zeros((1, NP)) + 1.0 / NP # init weight

  return px, pw

4、完整源码

该代码来源于https://github.com/AtsushiSakai/PythonRobotics

"""

Particle Filter localization sample

author: Atsushi Sakai (@Atsushi_twi)

"""

import math

import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.transform import Rotation as Rot

# Estimation parameter of PF
Q = np.diag([0.2]) ** 2 # range error
R = np.diag([2.0, np.deg2rad(40.0)]) ** 2 # input error

# Simulation parameter
Q_sim = np.diag([0.2]) ** 2
R_sim = np.diag([1.0, np.deg2rad(30.0)]) ** 2

DT = 0.1 # time tick [s]
SIM_TIME = 50.0 # simulation time [s]
MAX_RANGE = 20.0 # maximum observation range

# Particle filter parameter
NP = 100 # Number of Particle
NTh = NP / 2.0 # Number of particle for re-sampling

show_animation = True


def calc_input():
  v = 1.0 # [m/s]
  yaw_rate = 0.1 # [rad/s]
  u = np.array([[v, yaw_rate]]).T
  return u


def observation(x_true, xd, u, rf_id):
  x_true = motion_model(x_true, u)

  # add noise to gps x-y
  z = np.zeros((0, 3))

  for i in range(len(rf_id[:, 0])):

    dx = x_true[0, 0] - rf_id[i, 0]
    dy = x_true[1, 0] - rf_id[i, 1]
    d = math.hypot(dx, dy)
    if d <= MAX_RANGE:
      dn = d + np.random.randn() * Q_sim[0, 0] ** 0.5 # add noise
      zi = np.array([[dn, rf_id[i, 0], rf_id[i, 1]]])
      z = np.vstack((z, zi))

  # add noise to input
  ud1 = u[0, 0] + np.random.randn() * R_sim[0, 0] ** 0.5
  ud2 = u[1, 0] + np.random.randn() * R_sim[1, 1] ** 0.5
  ud = np.array([[ud1, ud2]]).T

  xd = motion_model(xd, ud)

  return x_true, z, xd, ud


def motion_model(x, u):
  F = np.array([[1.0, 0, 0, 0],
         [0, 1.0, 0, 0],
         [0, 0, 1.0, 0],
         [0, 0, 0, 0]])

  B = np.array([[DT * math.cos(x[2, 0]), 0],
         [DT * math.sin(x[2, 0]), 0],
         [0.0, DT],
         [1.0, 0.0]])

  x = F.dot(x) + B.dot(u)

  return x


def gauss_likelihood(x, sigma):
  p = 1.0 / math.sqrt(2.0 * math.pi * sigma ** 2) * \
    math.exp(-x ** 2 / (2 * sigma ** 2))

  return p


def calc_covariance(x_est, px, pw):
  """
  calculate covariance matrix
  see ipynb doc
  """
  cov = np.zeros((3, 3))
  n_particle = px.shape[1]
  for i in range(n_particle):
    dx = (px[:, i:i + 1] - x_est)[0:3]
    cov += pw[0, i] * dx @ dx.T
  cov *= 1.0 / (1.0 - pw @ pw.T)

  return cov


def pf_localization(px, pw, z, u):
  """
  Localization with Particle filter
  """

  for ip in range(NP):
    x = np.array([px[:, ip]]).T
    w = pw[0, ip]

    # Predict with random input sampling
    ud1 = u[0, 0] + np.random.randn() * R[0, 0] ** 0.5
    ud2 = u[1, 0] + np.random.randn() * R[1, 1] ** 0.5
    ud = np.array([[ud1, ud2]]).T
    x = motion_model(x, ud)

    # Calc Importance Weight
    for i in range(len(z[:, 0])):
      dx = x[0, 0] - z[i, 1]
      dy = x[1, 0] - z[i, 2]
      pre_z = math.hypot(dx, dy)
      dz = pre_z - z[i, 0]
      w = w * gauss_likelihood(dz, math.sqrt(Q[0, 0]))

    px[:, ip] = x[:, 0]
    pw[0, ip] = w

  pw = pw / pw.sum() # normalize

  x_est = px.dot(pw.T)
  p_est = calc_covariance(x_est, px, pw)

  N_eff = 1.0 / (pw.dot(pw.T))[0, 0] # Effective particle number
  if N_eff < NTh:
    px, pw = re_sampling(px, pw)
  return x_est, p_est, px, pw


def re_sampling(px, pw):
  """
  low variance re-sampling
  """

  w_cum = np.cumsum(pw)
  base = np.arange(0.0, 1.0, 1 / NP)
  re_sample_id = base + np.random.uniform(0, 1 / NP)
  indexes = []
  ind = 0
  for ip in range(NP):
    while re_sample_id[ip] > w_cum[ind]:
      ind += 1
    indexes.append(ind)

  px = px[:, indexes]
  pw = np.zeros((1, NP)) + 1.0 / NP # init weight

  return px, pw


def plot_covariance_ellipse(x_est, p_est): # pragma: no cover
  p_xy = p_est[0:2, 0:2]
  eig_val, eig_vec = np.linalg.eig(p_xy)

  if eig_val[0] >= eig_val[1]:
    big_ind = 0
    small_ind = 1
  else:
    big_ind = 1
    small_ind = 0

  t = np.arange(0, 2 * math.pi + 0.1, 0.1)

  # eig_val[big_ind] or eiq_val[small_ind] were occasionally negative
  # numbers extremely close to 0 (~10^-20), catch these cases and set the
  # respective variable to 0
  try:
    a = math.sqrt(eig_val[big_ind])
  except ValueError:
    a = 0

  try:
    b = math.sqrt(eig_val[small_ind])
  except ValueError:
    b = 0

  x = [a * math.cos(it) for it in t]
  y = [b * math.sin(it) for it in t]
  angle = math.atan2(eig_vec[1, big_ind], eig_vec[0, big_ind])
  rot = Rot.from_euler('z', angle).as_matrix()[0:2, 0:2]
  fx = rot.dot(np.array([[x, y]]))
  px = np.array(fx[0, :] + x_est[0, 0]).flatten()
  py = np.array(fx[1, :] + x_est[1, 0]).flatten()
  plt.plot(px, py, "--r")


def main():
  print(__file__ + " start!!")

  time = 0.0

  # RF_ID positions [x, y]
  rf_id = np.array([[10.0, 0.0],
           [10.0, 10.0],
           [0.0, 15.0],
           [-5.0, 20.0]])

  # State Vector [x y yaw v]'
  x_est = np.zeros((4, 1))
  x_true = np.zeros((4, 1))

  px = np.zeros((4, NP)) # Particle store
  pw = np.zeros((1, NP)) + 1.0 / NP # Particle weight
  x_dr = np.zeros((4, 1)) # Dead reckoning

  # history
  h_x_est = x_est
  h_x_true = x_true
  h_x_dr = x_true

  while SIM_TIME >= time:
    time += DT
    u = calc_input()

    x_true, z, x_dr, ud = observation(x_true, x_dr, u, rf_id)

    x_est, PEst, px, pw = pf_localization(px, pw, z, ud)

    # store data history
    h_x_est = np.hstack((h_x_est, x_est))
    h_x_dr = np.hstack((h_x_dr, x_dr))
    h_x_true = np.hstack((h_x_true, x_true))

    if show_animation:
      plt.cla()
      # for stopping simulation with the esc key.
      plt.gcf().canvas.mpl_connect(
        'key_release_event',
        lambda event: [exit(0) if event.key == 'escape' else None])

      for i in range(len(z[:, 0])):
        plt.plot([x_true[0, 0], z[i, 1]], [x_true[1, 0], z[i, 2]], "-k")
      plt.plot(rf_id[:, 0], rf_id[:, 1], "*k")
      plt.plot(px[0, :], px[1, :], ".r")
      plt.plot(np.array(h_x_true[0, :]).flatten(),
           np.array(h_x_true[1, :]).flatten(), "-b")
      plt.plot(np.array(h_x_dr[0, :]).flatten(),
           np.array(h_x_dr[1, :]).flatten(), "-k")
      plt.plot(np.array(h_x_est[0, :]).flatten(),
           np.array(h_x_est[1, :]).flatten(), "-r")
      plot_covariance_ellipse(x_est, PEst)
      plt.axis("equal")
      plt.grid(True)
      plt.pause(0.001)


if __name__ == '__main__':
  main()

到此这篇关于基于Python实现粒子滤波的文章就介绍到这了,更多相关Python实现粒子滤波内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！