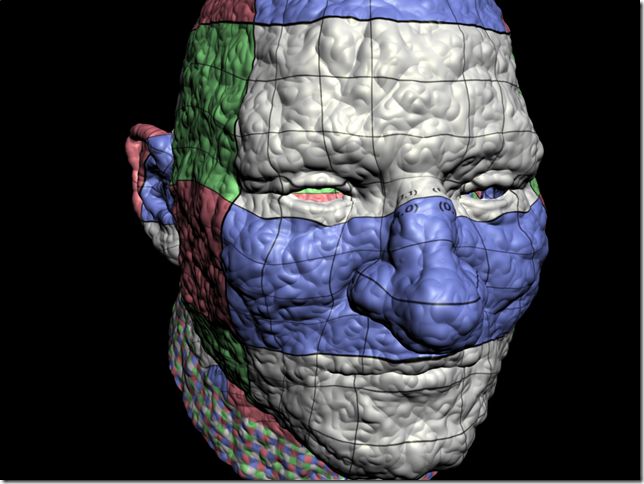
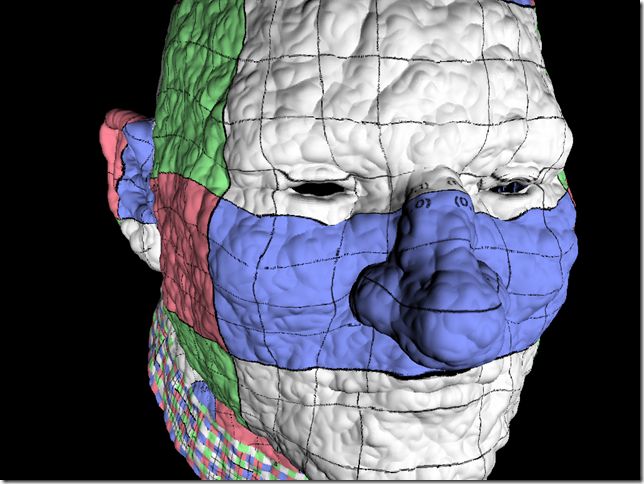
Direct Rendering RenderMan Point Cloud
版权所有人周波，本文仅供学习参考之用，任何网站组织若没有作者同意不得擅自转载本文以及相关章节包括图片。
- AO : Ambient Occlusion
- ID : Indirect Diffuse
- MR : Mesh Reconstruction
- MP : Micro Polygon
- RM : RenderMan
- RT : Ray Tracing
- SP : Shading Point
- PB : Point Based
- PR : Point Rendering
- PC : Point Cloud
- SUBD : Catmull-Clark Subdivision Surface
请勿饭后看此文，插图可能会导致对您健康的损害。想骂的随便。
商业版本的Pixar RenderMan从版本12开始支持bake场景点云，进行过滤以及贴图渲染，从版本13开始支持Fast Approximate Occlusion and Color Bleeding，也就是Point Based {Occlusion|Color Bleeding}。PBAO和PBID与基于RT的上古算法优点在于，速度快、效果可控、稳定性高。由于工作需要与个人兴趣，本人研究了一下RM中的PC以及点渲染技术，抛砖引玉，希望对大家能有所帮助。
Point Cloud Of RenderMan
首先总结如下：UV数值不可信、dPdu/v不可信、半径不可信。
在comp.graphics.renderman新闻组上有一组2000年的讨论，关于如何Dump Grid，吸引了多位业界人士的参与包括Larry Gritz、Matt Pharr。讨论的结果就是使用DSO写SHADEROP，这样当Shader执行的时候，由于传递给SHADEROP一个uniform参数，那么每个Grid实例会执行一次，于是就可以DUMP出每个Grid上的MP数据。源代码在Matt Pharr的个人网站上有，也就是一个很小的C文件，有兴趣的读者可以尝试使用一下。注意要仔细的看注释部分，否则运行时会有各种各样可以想得到的问题。
从RM的REYES管线中DUMP出的点云根据bake3d的参数而意义不同，如果启用了差值，那么每个点代表的近似为MP的中心，如果不差值那么就是Shading Point。每个网格边界其实是重合的，这样我们看到的Shading结果才是平滑无缝的。如果我们把大而完整的网格称为“品质好”的网格，那么由应用于游戏的三角形模型Dice后生成的网格就可以用“惨不忍睹”来形容。NURBS的最优秀，SUBD其次，因为SUBD对原始模型进行求精。参考PIXIE和Aqsis的实现代码我们可以知道，对于参数化模型来说，DICE过程异常简单，只需要沿着UV方向采样就可以了。对于基于三角形面片的模型来说，是通过Object Coordinate中的顶点数据进行DICE，每个三角形拥有一组独立的UV。最终每个网格会有(udivide+1)*(vdivide+1)大小的Grid，倘若大于当前GRID_MAXSIZE的限制，那么就一分为二继续Dice。当REYES管线通过Dice获得了足够多的SP，下一步就是渲染，尔后插值Grid这个Patch并光栅化之，所以无论Shading Rate多高，我们总是能够获得平滑的模型，但是颜色成分却丢失不少。不过由于高素质的Displacement往往需要比较小的Shading Rate，所以上面我提高的那种极端情况几乎不可能见到，否则不如用Maya Hardware Renderer了。
按道理说一个独立的Grid应该只有一组独立的UV参数化坐标，将UV带入Quadric Grid将必然获得独立的P。经过仔细的尝试我发现，这种理想的情况几乎是不可能的，除非NURBS，一旦Dice使用Polygon非SUBD的实际模型，几乎是必然的，上面提高的那个DSO会导致RM的崩溃。经过测试还发现连NaN这种几户不可能出现的数值也会在结果中出现。所以我推荐，倘若想处理点云，最好将模型转为SUBD或者完全使用NURBS进行建模绑定动画，只不过这个难度，嘿嘿～
REYES输出的这些顶点的半径根本不精确。假如我们不差值，严格来说它应该等于dPdu*Du或者dPdv*dv，也就是分别代表UV方向上和下一个SP的距离。在RenderMan附带的PtViewer这个小工具中，经过我的DEBUG发现它的FACET模式仅仅是首先绘制一个[-1,1]^2的正方形，尔后根据顶点的半径数值进行缩放，每个顶点承载同样的颜色。虽然说这样的渲染方式比较粗劣，但是却符合RenderMan的渲染思路。
总之，我们从REYES获得的点云是一个除了P、N可信外，其他参数都不可行的数据集。
特别的，我们可以编译一个DEBUG版本的Aqsis，这样每次渲染RM都会将DICE结果输出保存。
Dispers Elfen
至此，我们已经充分了解了RM PC的一些重要特征，下面开始渲染。
方向总共有两个，一条路通向PR，另外一条路通向MR。前者的速度快，处理难度小，素质稳定；后者在于彻底解决一切问题，直接使用GPU光栅化模型，但是速度慢，难度大，素质不可控。下面将详细的阐述两类方法。
Point Based Rendering
PBR的核心思路在于，使用Vertex Shader实时计算每个离散点所应该覆盖的像素大小进行缩放，最终获得光栅化结果。如右图。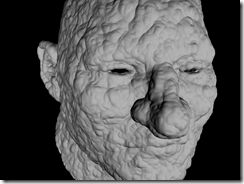 
显而易见的，使用PBR渲染得到的模型要比原始的模型大一些，而且局部细节可能会丢失。下面主要介绍时髦的EWA Splatting渲染方式。详细内容请参阅Matthias Zwicker的博士论文。
假如我们想通过利用点的坐标及法线构造出的Disk拼凑模型，那么几乎是必然的要进行Disk的半径计算和交叠部分的过滤。从微分几何我们可以知道一个足够小的椭圆是最接近于微分面。所以我们可以在每个顶点处构造一个Disk或者Ellipses进行对原始模型的逼近。由于每个面片可能会覆盖多个区域，所以最终Disk贡献到的像素中心离Disk的中心都会有距离，由此构造出过滤器，EWA使用的是Gaussian过滤器。经过BLEND后除以权重，由此我们就获得了经过过滤的图。由于Disk的大小是可以调整的，Gaussian过滤器大小也是可以调整的，所以最终效果会随着模型的不同、渲染要求的不同而不 同。这里有样图，原理大家一目了然。
ARB_point_sprite这个OpenGL拓展用于高效率的处理实时渲染中的粒子部分，利用这个拓展渲染点的性能比启用GL_POINT_SMOOTH高出不少。我们使用这个拓展进行屏幕空间内的快速插值，获取纹理坐标（详细请看NVIDIA OpenGL Extension Specifications）。
Mesh Reconstruction
总结为一句话：MR是计算几何与数值分析的综合。
这里的计算几何知识主要包括Principal Component Analysis （PCA）、Delaunay Triangulation（DT）、Implicit Surface（IS）。数值分析主要是Moving Least Square（MLS）。
隐函数的概念来自于数学分析，我们可以简单的理解为，离散点构造了一个函数，这个函数的性质是倘若f(x) = 0，那么x就在模型上，如果f>0那么x就在模型内部，反之就在模型外部。本质上可以理解为是离散数据插值问题。IS还有一个流行应用就是CFD。我们可以用Radial Basis Function（RBF）来表现IS，详细的实现过程请参阅Patrick Reuter的博士论文。MLS更加将问题更加的线性化，它的主要思路就是假想离散点构造出了一个曲面，然后将外表面上的一点投射到这个曲面上，得到的结果就是原始模型的一部分。MLS的效率极低，这里有巴西学者的实现。本质上属于非线性优化问题，使用GSL进行迭代计算。
值得一题的是，《Visualization of Point-Based Surfaces with Locally Reconstructed Subdivision Surfaces》这篇论文中提到的方法倒是值得使用，具体过程如下：
- 使用八叉数分割点云
- 计算每个八叉数节点的中点和平均方向，构造切线平面
- 将空间中的点投射到切线平面上，进行2D DT
- 将2D平面上的点投射回三维空间并运用SUBD的方法进行模型求精
详细的请看那篇论文，再次不再过多复述。
State The Shit Of
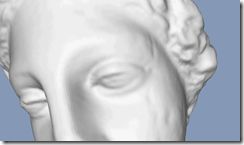
由于一些不可知的奇怪原因，倘若使用RM计算一个超大幅面的AO Pass，比如5k^2，那么RM有可能会因为不释放内存而崩溃。由于目前大部分PC都是32bit，单独进程空间最多可以分配不到2G的内存，所以即使使用PB AO依旧有点云数目的限制。RM自带的PtFilter会因为无法分配足够的内存存放点云数据而拒绝执行。调整Shading Rate则可以，但是那样属于牺牲素质的方式。我觉得倘若使用GPU进行Point Splatting，那么必须进行类似Gelato的超采样，对比RM的乱续采样，倘若使用规律采样，样本数目足够多的时候是和RM的素质不相上下的。这里引用的对比是RM和OpenGL没有经过任何过滤处理的图片，大家可以看得出来差距。所有的论文都没有提供原始大图，没有使用任何能够明显表现素质诧异的纹理贴图，不得不说明是一种敷衍。
注意：Shader不同导致照明结果不同，通过渲染这个经过Displacement的模型，根本的素质差异还是一眼就可以看出的。由于点密度极大的影响GPU渲染的素质，而且没有任何屏幕抗锯齿的措施，导致头像脖子部分高频部分依旧残留，而RM的图片则都被过滤去掉了。我想经过32x32的Supersampling，GPU光栅化的素质完全可以和RM一比，这样对Cinematic Relighting的预览极其的有益。这个是我以前做的一个类似Gelato的玩意渲染的图，将它加入点云渲染管线的末端应该可以极大的提高素质。
Useful Link
大家Google去吧。
CGAL
QHull
GNU Scientific Library
GNU Octave
PIXIE
Aqsis
ETH Graphics Department
INRIA
Germany RWTH Achen Computer Graphics Group